堆数据结构:什么是堆?最小堆和最大堆(示例)
什么是堆?
堆是一种特殊的树状数据结构。堆由称为根(父节点)的最高节点组成。它的第二个子节点是根的左子节点,而第三个节点是根的右子节点。后续节点从左到右填充。父节点键与子节点进行比较,并进行适当的排列。树易于可视化,其中每个实体都称为节点。节点具有唯一的键用于标识。
为什么需要堆数据结构?
以下是使用堆数据结构的主要原因
- 堆数据结构允许在对数时间内进行删除和插入操作 - O(log2n)。
- 树中的数据以特定顺序排列。除了更新或查询最大值或最小值等内容外,程序员还可以找到父节点和子节点之间的关系。
- 您可以应用文档对象模型的概念来帮助您理解堆数据结构。
堆的类型
堆数据结构有各种算法来处理堆数据结构中的插入和删除元素,包括优先级队列、二叉堆、二项堆和堆排序。
- 优先级队列:它是一种抽象数据结构,包含优先排序的对象。每个对象或项都有为其预先排序的优先级。因此,分配了较高优先级的对象或项比其他对象或项先得到服务。
- 二叉堆:二叉堆适用于简单的堆操作,如删除和插入。
- 二项堆:二项堆由一系列构成堆的二项树集合组成。二项堆树不是普通树,因为它经过严格定义。二项树中的元素总数始终拥有 2n 个节点。
- 堆排序:与大多数排序算法不同,堆排序在其排序操作中使用了 O(1) 的空间。它是一种基于比较的排序算法,通过首先将其转换为最大堆来按升序进行排序。您可以将堆排序视为升级版的二叉搜索树。
通常,堆数据结构采用两种策略。对于输入 12 – 8 – 4 – 2 和 1
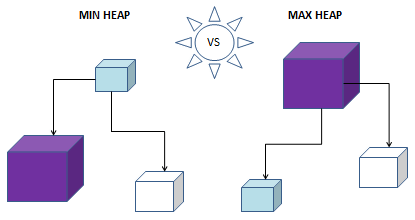
- 最小堆 - 最小值在顶部
- 最大堆 - 最大值在顶部
最小堆
在最小堆结构中,根节点的值等于或小于其子节点。最小堆的此堆节点包含最小值。总而言之,其最小堆结构是一个完整的二叉树。
一旦在树中有了最小堆,所有叶子节点都是有效的候选者。但是,您需要检查每个叶子节点才能获得精确的最大堆值。
最小堆示例
在上面的图表中,您可以注意到从根到最低节点的明显顺序。
假设您将元素存储在数组 Array_N[12,2,8,1,4] 中。从数组中可以看出,根元素违反了最小堆的优先级。为了维护最小堆属性,您必须执行最小堆化操作来交换元素,直到满足最小堆属性。
最大堆
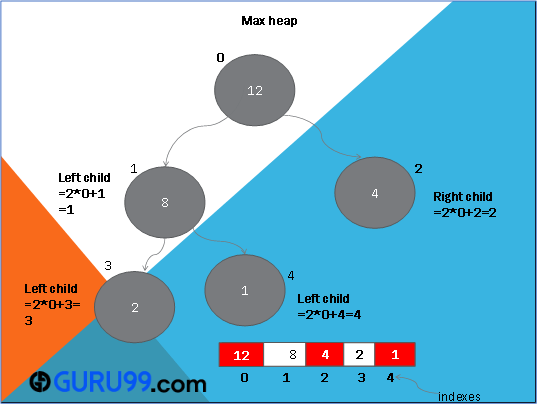
在最大堆的结构中,父节点或根节点的值等于或大于其节点中的子节点。该节点包含最大值。此外,它是一个完全二叉树,因此您可以从一组值构建最大堆,并在 O(n) 时间内运行它。
以下是实现 Java 最大堆的几种方法
- Add():将新元素放入堆中。如果您使用数组,对象将被添加到数组的末尾,而在二叉树中,对象将从上到下添加,然后从左到右添加。
- Remove():此方法允许您从数组列表中删除第一个元素。由于新添加的元素不再是最大的,Sift-Down 方法会将其移到新位置。
- Sift-Down():此方法将根对象与其子节点进行比较,然后将新添加的节点移到其正确的位置。
- Sift-Up():如果您使用数组方法将新插入的元素添加到数组中,则 Sift-Up 方法有助于新添加的节点重新定位到其新位置。新插入的项首先与父节点进行比较,模拟树数据结构。
应用公式 Parent_Index=Child_Index/2。您继续执行此操作,直到最大元素位于数组的前面。
基本堆操作
为了在数据集中查找最高和最低值,您需要许多基本堆操作,例如查找、删除和插入。由于元素会不断地进出,您必须
- 查找 - 在堆中查找项。
- 插入 - 将新子项添加到堆中。
- 删除 - 从堆中删除节点。
创建堆
构建堆的过程称为创建堆。给定一个键列表,程序员会创建一个空堆,然后使用基本堆操作一次插入其他键。
因此,让我们开始使用 William 的方法通过将值 12、2、8、1 和 4 插入堆来构建一个最小堆。您可以通过从一个空堆开始,然后用 O (nlogn) 的时间依次填充其他元素来构建一个包含 n 个元素的堆。
- Heapify:在插入算法中,它有助于将元素插入堆。检查是否遵循了堆数据结构中强调的属性。
例如,最大堆化会检查父节点的值是否大于其子节点。然后可以使用交换等方法对元素进行排序。
- 合并:考虑到您有两个堆需要合并成一个,请使用合并堆将来自两个堆的值合并在一起。但是,原始堆仍然被保留。
检查堆
检查堆是指检查堆数据结构中的元素数量,并验证堆是否为空。
检查堆很重要,就像对元素进行排序或排队一样。使用 Is-Empty() 检查是否有要处理的元素很重要。堆的大小有助于定位最大堆或最小堆。因此,您需要知道遵循堆属性的元素。
- Size - 返回堆的大小或长度。您可以知道有多少元素按排序顺序排列。
- Is-empty - 如果堆为 NULL,则返回 TRUE,否则返回 FALSE。
在这里,您将打印优先级队列中的所有元素,然后检查优先级队列不为空。
//print head the head values
While (!priorityQ.isEmpty()) {
System.out.print(priorityQ.poll()+" ");
堆数据结构的使用
堆数据结构在许多实际编程应用中有用,例如
- 有助于垃圾邮件过滤。
- 实现图算法。
- 操作系统负载均衡和数据压缩。
- 查找统计数据中的顺序。
- 实现优先级队列,您可以在其中以对数时间搜索列表中的项。
- 堆数据结构也用于排序。
- 模拟队列中的客户。
- 在操作系统中进行中断处理。
- 在 Huffman 编码中用于数据压缩。
堆优先级队列属性
- 在优先堆中,列表中的数据项相互比较以确定较小的元素。
- 将元素放入队列然后移除。
- 优先级队列中的每个元素都有一个与其相关的唯一数字,称为优先级。
- 当退出优先级队列时,最高优先级的元素先退出。
在Java中实现堆优先级队列的步骤
Java 中的堆排序及代码示例
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] arr = {5, 9, 3, 1, 8, 6};
// Sort the array using heap sort
heapSort(arr);
// Print the sorted array
System.out.println(Arrays.toString(arr));
}
public static void heapSort(int[] arr) {
// Convert the array into a heap
for (int i = arr.length / 2 - 1; i >= 0; i--) {
heapify(arr, arr.length, i);
}
// Extract the maximum element from the heap and place it at the end of the array
for (int i = arr.length - 1; i >= 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
heapify(arr, i, 0);
}
}
public static void heapify(int[] arr, int n, int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Find the largest element among the root, left child, and right child
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// If the largest element is not the root, swap the root and the largest element and heapify the sub-tree
if (largest != i) {
int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
heapify(arr, n, largest);
}
}
}
输出
Original Array: 5 9 3 1 8 6 Heap after insertion: 9 8 6 1 5 3 Heap after sorting: 1 3 5 6 8 9
Python 中的堆排序及代码示例
def heap_sort(arr):
"""
Sorts an array in ascending order using heap sort algorithm.
Parameters:
arr (list): The array to be sorted.
Returns:
list: The sorted array.
"""
n = len(arr)
# Build a max heap from the array
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
# Extract elements from the heap one by one
for i in range(n - 1, 0, -1):
arr[0], arr[i] = arr[i], arr[0] # swap the root with the last element
heapify(arr, i, 0) # heapify the reduced heap
return arr
def heapify(arr, n, i):
"""
Heapifies a subtree with the root at index i in the given array.
Parameters:
arr (list): The array containing the subtree to be heapified.
n (int): The size of the subtree.
i (int): The root index of the subtree.
"""
largest = i # initialize largest as the root
left = 2 * i + 1 # left child index
right = 2 * i + 2 # right child index
# If left child is larger than root
if left < n and arr[left] > arr[largest]:
largest = left
# If right child is larger than largest so far
if right < n and arr[right] > arr[largest]:
largest = right
# If largest is not root
if largest != i:
arr[i], arr[largest] = (
arr[largest],
arr[i],
) # swap the root with the largest element
heapify(arr, n, largest) # recursively heapify the affected subtree
arr = [4, 1, 3, 9, 7]
sorted_arr = heap_sort(arr)
print(sorted_arr)
输出
[1, 3, 4, 7, 9]
接下来,您将学习二分法
摘要
- 堆是一种特殊的树状数据结构。让我们想象一个有父母和孩子的家谱。
- Java 中的堆数据结构允许在对数时间内进行删除和插入操作 - O(log2n)。
- Python 中的堆具有各种算法来处理堆数据结构中的插入和删除元素,包括优先级队列、二叉堆、二项堆和堆排序。
- 在最小堆结构中,根节点的值等于或小于其子节点。
- 在最大堆结构中,根节点(父节点)的值等于或大于其节点中的子节点。
- 检查堆是指检查堆数据结构中的元素数量,并验证堆是否为空。