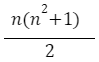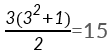幻方 – 使用 C & Python 示例解决 3×3 难题

什么是幻方？

幻方是一种具有特殊数字排列的方阵。这些数字的排列使得每条对角线、每行和每列的数字之和都相等。幻方游戏是用于休闲数学的简单逻辑谜题。

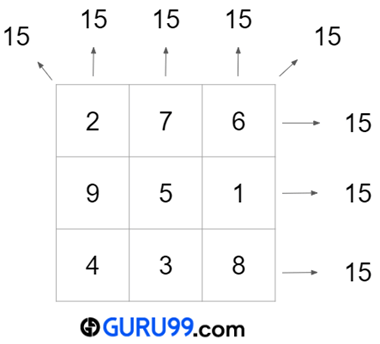
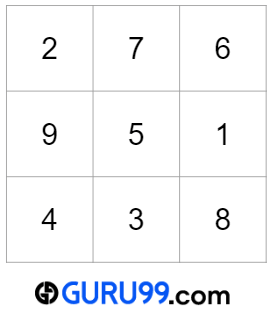
幻方示例

$Magic Square$

上图是三阶幻方的一个例子。每条对角线、每行和每列的和都是15。

幻方如何工作

幻方是n*n的矩阵，包含n^2个正整数。方阵的行数或列数称为矩阵的阶。

通常，幻方谜题的阶数为奇数，并包含从1到n^2的整数。每条对角线、每行和每列的和都相同。这个数字称为幻和或魔术常数。一般而言，此幻和取决于矩阵的阶。阶为n的幻方的幻和公式是：

以三阶幻方为例，其幻和将是：

为什么它们被称为“幻”方？

古代数学家们被一些有趣的数字组合的性质所吸引。幻方就是其中之一。最早的幻方证据可以追溯到公元前190年的中国。

一些研究表明，古代日本、印度和阿拉伯地区也存在幻方谜题。根据一些传说，人们曾认为这些特殊的数字组合与魔法世界有关。因此，这些方阵被称为幻方。

幻方的类型

幻方数学有几种不同的变体：

标准幻方： 此类幻方包含前n^2个数字。
半幻方： 在此类型中，只有行和列的和等于幻和。
简单幻方： 与前一种类型相比，行、列和两条对角线的和都等于幻和。
最完美幻方： 这是一个具有两个特殊属性的标准幻方。在这里，矩阵中的每个2x2子矩阵的和为2(n^2+1)。并且，网格中相隔n/2个方格的任意一对数字之和为n^2+1。

基于属性，还有更多类型的幻方。但每当我们只提到幻方时，我们假设它是奇数阶的标准简单幻方。

生成幻方的算法

生成奇数阶幻方的算法是

第一个数字1将存储在(n/2, n-1)位置，其中第一个坐标是行位置，第二个坐标是列位置。在后续步骤中，我们将此位置表示为(x, y)。
接下来的数字将存储在(x-1, y+1)位置。如果该位置无效，我们将考虑以下条件。
1. 如果行位置为-1，它将回绕到n-1。同样，如果计算出的列位置为n，它将回绕到0。
2. 如果计算出的位置已包含数字，则行位置将增加1，列位置将减2。
3. 如果行位置为-1且相应的列位置为n，则新位置将是(0, n-2)。

注意：此算法仅生成奇数阶的有效幻方。我们也认为这种幻方是包含前n^2个数字的标准幻方。此外，对于相同的n值，可能存在多个解决方案。

让我们举一个例子，看看它是如何工作的。假设我们要找到三阶幻方。由于它是一个简单而标准的奇数阶幻方，它将包含从1到3^2或9的所有数字。

它是如何工作的？

根据我们的算法，步骤将如下所示：

步骤1） 第一个数字1将位于(3/2, 3-1)或(1, 2)位置。按照惯例，在后续步骤中，将x设为1，y设为2。

步骤2） 其余数字的位置将按以下方式计算：

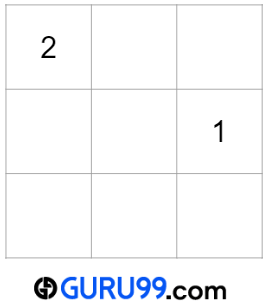
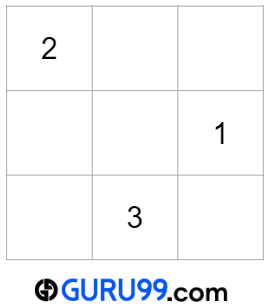
数字2的位置

下一个数字将位于(x-1, y+1)或(0, 3)位置，这是一个无效位置。根据条件(a)，相应的有效位置将是(0,0)。所以，x=0，y=0。

数字3的位置

数字3将位于(x-1, y+1)或(-1, 1)位置，这是一个无效位置。根据条件(a)，有效的行位置将是n-1或2。所以，数字3将位于(2, 1)。对于下一个数字，x=2，y=1。

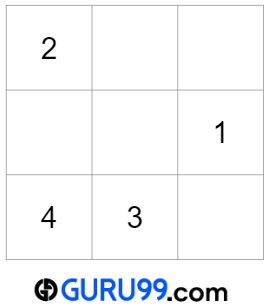
数字4的位置

数字4应该位于(x-1, y+1)或(1, 2)位置，这是一个有效位置。但是该位置已包含数字。根据条件(b)，有效位置将是(1+1, 2-2)或(2,0)。对于下一个数字，x=2，y=0。

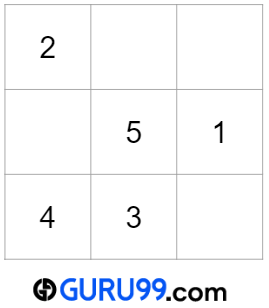
数字5的位置

数字5应该位于(x-1, y+1)或(1, 1)位置，这是一个有效位置。对于下一个数字，x=1，y=1。

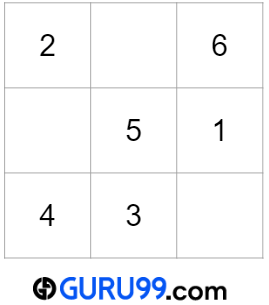
数字6的位置

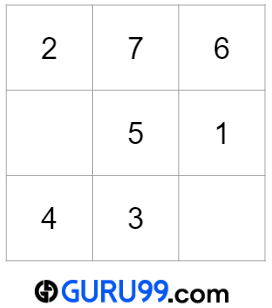
数字6应该位于(x-1, y+1)或(0, 2)位置，这是一个有效位置。对于下一个数字，x=0，y=2。

数字7的位置

数字7应该位于(x-1, y+1)或(-1, 3)位置，这是一个无效位置。根据条件(c)，有效位置将是(0, n-2)或(0, 1)。对于下一个数字，x=0，y=1。

数字8的位置

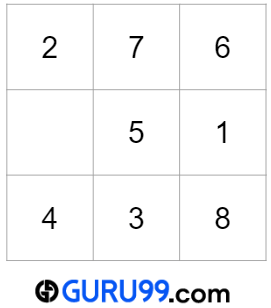
数字8应该位于(x-1, y+1)或(-1, 2)位置，这是一个无效位置。根据条件(a)，有效位置将是(2, 2)。对于下一个数字，x=2，y=2。

数字9的位置

数字9应该位于(x-1, y+1)或(1, 3)位置，这是一个无效位置。根据条件(a)，有效位置将是(1, 0)。

伪代码

Begin
	Declare an array of size n*n
	Initialize the array to 0
	Set row = n/2
	Set column = n-1
	For all number i: from 1 to n*n
		If the row = -1 and column = n
			row = 0
			column = n-2
		Else
			If row = -1
				row = n-1
			If column = n
				column = 0
		If the position already contains a number
			decrement column by 2
			increment row by 1
			continue until the position is not 0
		Else
			put the number i into the calculated position
			increment i		
		Increment column value
		Decrement row value
End

C++ 幻方代码

输入

/*
A C/C++ program for generating odd order magic squares
*/
#include <bits/stdc++.h>
using namespace std;

void GenerateMagicSquare(int n)
{
    int magic[n][n];
    //initializing the array
    for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
	        magic[i][j] = 0;
    //setting row and column value
    int i = n / 2;
    int j = n - 1;
    for (int k = 1; k <= n * n;) 
    {
//checking condition (c)
	if (i == -1 && j == n) 
	{
		j = n - 2;
		i = 0;
	}
	else 
	{
		//checking condition (a)
		if (j == n)
			j = 0;
		if (i < 0)
			i = n - 1;
		}
		//checking condition (b)
		if (magic[i][j]) 
		{
			j -= 2;
			i++;
			continue;
		}
		else
		{
		   	//placing the number into the array
		   	magic[i][j] = k; 
			k++;
		}	
		//for the next number setting (i-1, j+1)
		j++;
		i--; 
	}
	//printing the matrix
	for (int i = 0; i < n; i++)
 {
		for (int j = 0; j < n; j++)
			cout << magic[i][j] << "  ";
		cout << endl;
	}	
}
int main()
{
	//This code works for only odd numbers
	int n = 7;
	cout<<"The magic sum is " << n*(n*n+1)/2 <<endl;
	GenerateMagicSquare(n);
	return 0;
}

示例输出

The magic sum is 175

20  12  4  45  37  29  28
11  3  44  36  35  27  19
2  43  42  34  26  18  10
49  41  33  25  17  9  1
40  32  24  16  8  7  48
31  23  15  14  6  47  39
22  21  13  5  46  38  30

Python 幻方代码

def GenerateMagicSquare(n):
#initializing the array
	magic = [[0 for x in range(n)]
				for y in range(n)]
	#setting row and column value
	i = n // 2
	j = n - 1
	k = 1
	while k <= (n * n):
	    #checking condition (c)
		if i == -1 and j == n: 
			j = n - 2
			i = 0
		else:
			#checking condition (a)
			if j == n:
				j = 0
			if i < 0:
				i = n - 1
        #checking conditon (b)
		if magic[i][j]: 
			j = j - 2
			i = i + 1
			continue
		else:
		    #placing the number into the array
			magic[i][j] = k
			k = k + 1
        #for the next number setting (i-1, j+1)
		j = j + 1
		i = i - 1 
	#printing the matrix
	for i in range(0, n):
		for j in range(0, n):
			print('%2d ' % (magic[i][j]),end='')
			if j == n - 1:
				print()
#This code works for only odd numbers
n = 7
print("The magic sum is ",n * (n * n + 1) // 2, "\n")
GenerateMagicSquare(n)