B树在数据结构中的搜索、插入、删除操作示例

作者： Sarah Chen Sarah Chen
小时 - 权威教程 更新于

什么是 B 树？

B 树是一种自平衡数据结构，它遵循一套特定的规则，以更快、更节省内存的方式来搜索、插入和删除数据。为了实现这一点，遵循以下规则来创建 B 树。

B 树是一种特殊类型的树形数据结构。1972 年，McCreight 首次介绍了这种方法，Bayer 将其命名为高度平衡的 m 路查找树。它有助于保持数据排序，并允许在更短的时间内进行插入、搜索和删除等各种操作。

B 树的规则

以下是创建 B_Tree 的重要规则

  • 所有叶子节点都将在同一层创建。
  • B 树由一个称为“阶”的次数决定（由外部执行者，如程序员指定），该次数也称为“阶”
    m

    开始。值

    m

    取决于主要位于数据所在的磁盘块大小。

  • 节点的左子树将具有小于右子树的值。这意味着节点也从左到右按升序排序。
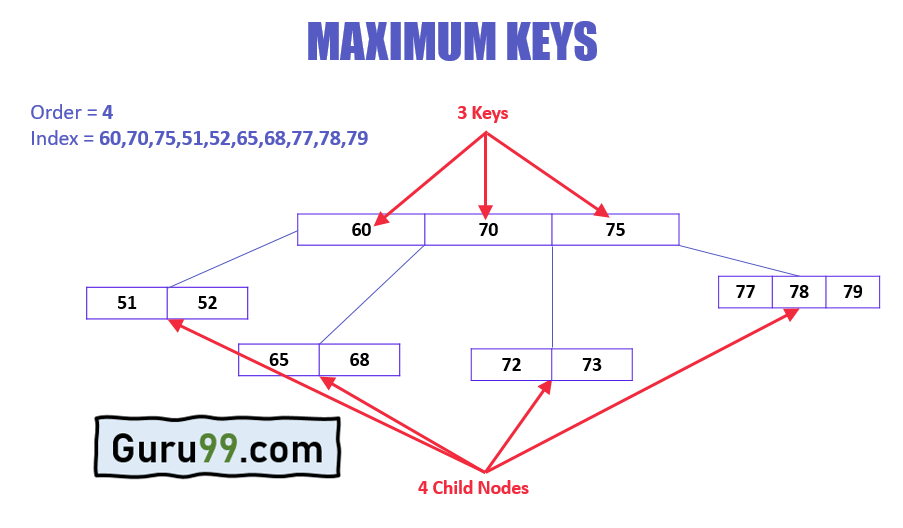
  • 根节点及其子节点可以包含的最大子节点数量通过以下公式计算
    m – 1

    例如

    m = 4
max keys: 4 – 1 = 3

Rules for B-Tree

  • 除根节点外，每个节点必须包含最小键数
    [m/2]-1

    例如

    m = 4
min keys: 4/2-1 = 1
  • 节点可以拥有的最大子节点数量等于其阶，即
    m
  • 节点可以拥有的最小子节点数是阶的一半，即 m/2（取天花板值）。
  • 节点中的所有键均按升序排序。

为什么使用 B 树

以下是使用 B 树的原因

  • 减少磁盘读取次数
  • B 树可以轻松优化以根据磁盘大小调整其大小（即子节点数量）
  • 它是专门为处理大量数据而设计的一种技术。
  • 它是数据库和文件系统的有用算法。
  • 在读写大量数据时，这是一个不错的选择

B 树的历史

  • 数据存储在磁盘块中，这些数据被加载到主内存（或 RAM）中时称为数据结构。
  • 对于海量数据，在磁盘中搜索一个记录需要读取整个磁盘；由于高磁盘访问频率和数据大小，这会增加时间和主内存消耗。
  • 为了克服这一点，会创建索引表，该表根据记录所在的块来保存记录的引用。这大大减少了时间和内存消耗。
  • 由于我们拥有海量数据，因此可以创建多级索引表。
  • 多级索引可以通过使用 B 树来设计，以自平衡的方式保持数据排序。

搜索操作

搜索操作是 B 树上最简单的操作。

应用以下算法

  • 将要搜索的键（值）设为“k”。
  • 从根开始搜索，并递归地向下遍历。
  • 如果 k 小于根节点的值，则搜索左子树；如果 k 大于根节点的值，则搜索右子树。
  • 如果节点包含找到的 k，则简单地返回该节点。
  • 如果节点中未找到 k，则向下遍历到具有更大键的子节点。
  • 如果树中未找到 k，则返回 NULL。

插入操作

由于 B 树是自平衡树，因此您不能强制将键插入任何节点。

应用以下算法

  • 运行搜索操作并找到合适的插入位置。
  • 将新键插入到正确的位置，但如果节点已包含最大数量的键
  • 节点将连同新插入的键一起，从中间元素分裂。
  • 中间元素将成为其他两个子节点的父节点。
  • 节点必须按升序重新排列键。
提示 以下关于插入算法的说法不正确

由于节点已满，因此会分裂，然后插入新值

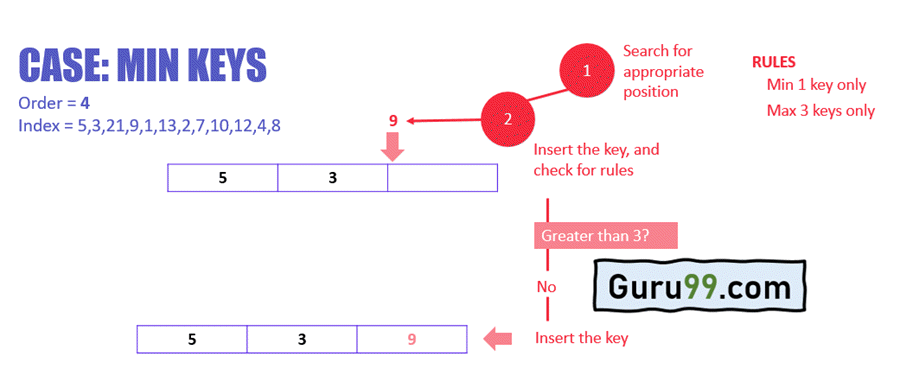
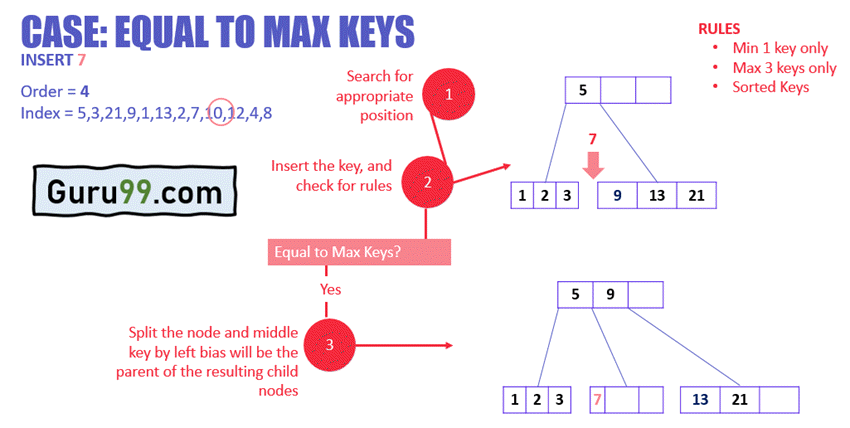
Insert Operation

在上面的示例中

  • 搜索节点中键的合适位置
  • 将键插入目标节点，并检查规则
  • 插入后，节点是否包含的键数大于或等于最小值 1？在这种情况下，是的。检查下一条规则。
  • 插入后，节点是否包含的键数大于最大键数 3？在这种情况下，否。这意味着 B 树没有违反任何规则，插入已完成。

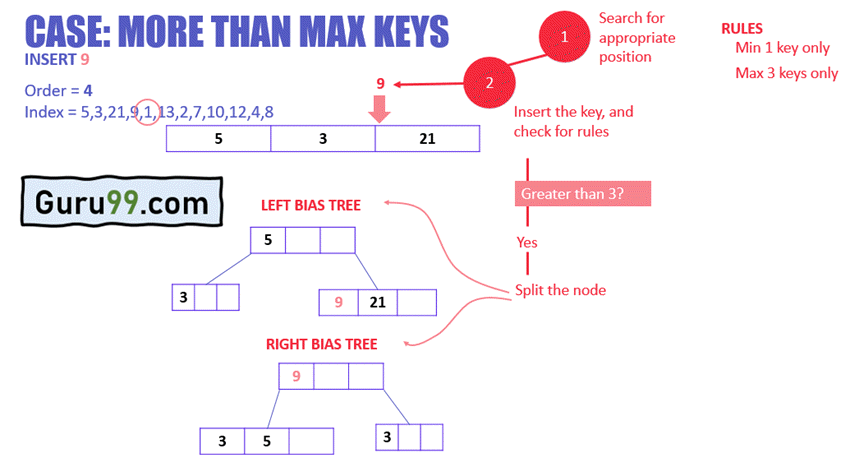
Insert Operation

在上面的示例中

  • 节点已达到最大键数
  • 节点将分裂，中间键将成为其余两个节点的主节点。
  • 如果键的数量是偶数，则中间节点将通过左偏或右偏选择。

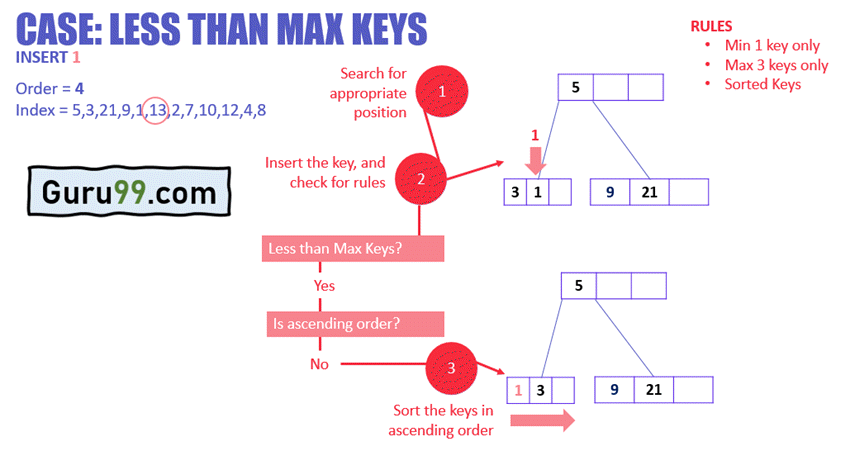
Insert Operation

在上面的示例中

  • 节点包含的键少于最大键数
  • 1 被插入到 3 旁边，但升序规则被违反
  • 为了解决这个问题，键被排序

同样，13 和 2 可以轻松地插入到节点中，因为它们满足节点的最大键数规则。

Insert Operation

在上面的示例中

  • 节点包含的键等于最大键数。
  • 将键插入目标节点，但违反了最大键数规则。
  • 目标节点被分裂，通过左偏的中间键现在是新子节点的父节点。
  • 新节点按升序排列。

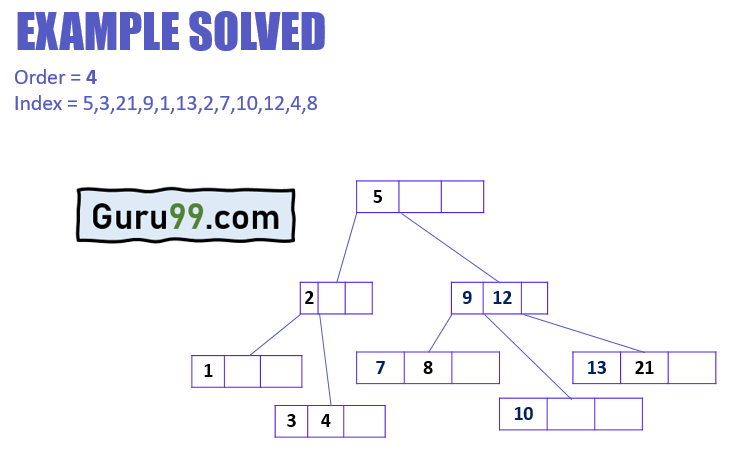
同样，根据上述规则和案例，其余值可以轻松地插入 B 树。

Insert Operation

删除操作

删除操作的规则比插入和搜索操作多。

应用以下算法

  • 运行搜索操作并找到节点中的目标键
  • 根据目标键的位置应用三个条件，如下节所述

如果目标键在叶节点中

  • 目标在叶节点中，键数多于最小值。
  • 删除此键不会违反 B 树的属性
  • 目标在叶节点中，它有最小键数
  • 删除此键会违反 B 树的属性
  • 目标节点可以从其紧邻的左节点或紧邻的右节点（兄弟节点）借用键
  • 如果兄弟节点具有的键数多于最小值，则它会说“是”
  • 将从父节点借用键，最大值将转移到父节点，父节点的最大值将转移到目标节点，然后删除目标值
  • 目标在叶节点中，但没有兄弟节点具有多于最小数量的键
  • 搜索键
  • 与兄弟节点和最小父节点合并
  • 总键数现在将多于最小值
  • 目标键将被父节点的最小值替换

如果目标键在内部节点中

  • 选择中序前驱或中序后继
  • 如果是中序前驱，则选择其左子树中的最大键
  • 如果是中序后继，则选择其右子树中的最小键
  • 只有当目标键的中序前驱的键数多于最小值时，它才能用中序前驱的最大值替换目标键
  • 如果目标键的中序前驱的键数不大于最小值，则查找中序后继的最小值。
  • 如果目标键的中序前驱和后继都少于最小值，则合并前驱和后继。

如果目标键在根节点中

  • 替换为中序前驱子树中的最大元素
  • 如果删除后，目标键的键数少于最小值，则目标节点将通过兄弟节点的父节点从其兄弟节点借用最大值。
  • 父节点的最大值将被目标节点获取，但会与兄弟节点的最大值节点一起。

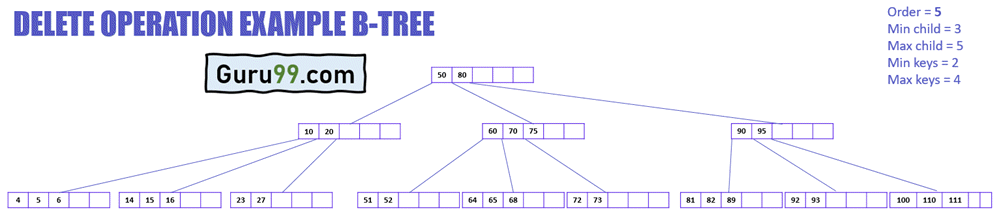
现在，让我们通过一个例子来理解删除操作。

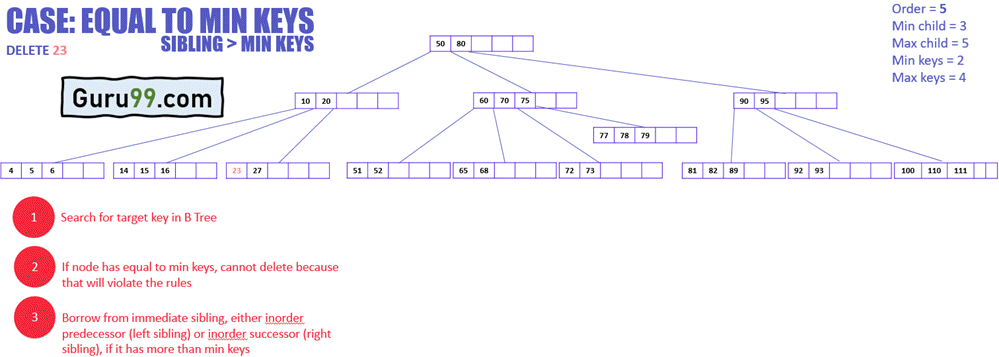
Delete Operation

上图显示了 B 树中删除操作的不同情况。此 B 树的阶为 5，这意味着任何节点可以拥有的最小子节点数为 3，而任何节点可以拥有的最大子节点数为 5。而任何节点可以拥有的最小和最大键数分别为 2 和 4。

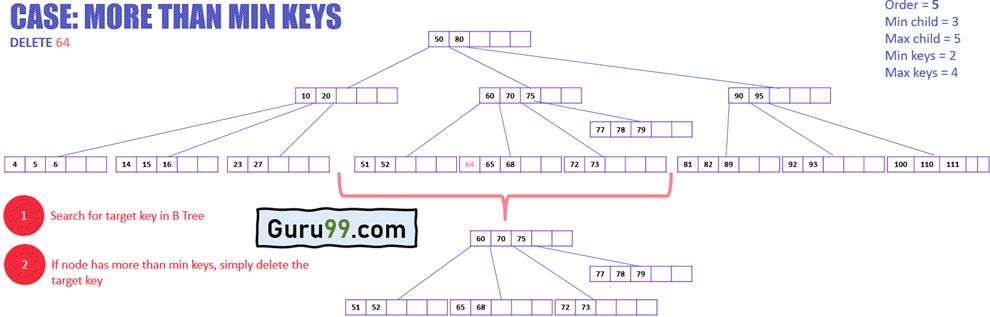
Delete Operation

在上面的示例中

  • 目标节点包含要删除的目标键
  • 目标节点包含的键数多于最小值
  • 直接删除键

Delete Operation

在上面的示例中

  • 目标节点包含的键数等于最小值，因此不能直接删除，因为这会违反条件

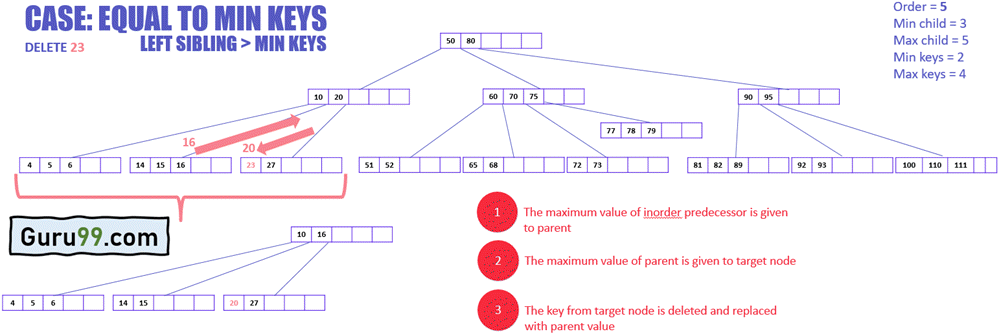
现在，下图解释了如何删除此键

Delete Operation

  • 目标节点将从其紧邻的兄弟节点借用一个键，在这种情况下，中序前驱（左兄弟节点），因为它没有中序后继（右兄弟节点）
  • 中序前驱的最大值将转移到父节点，父节点将最大值转移到目标节点（参见下图）

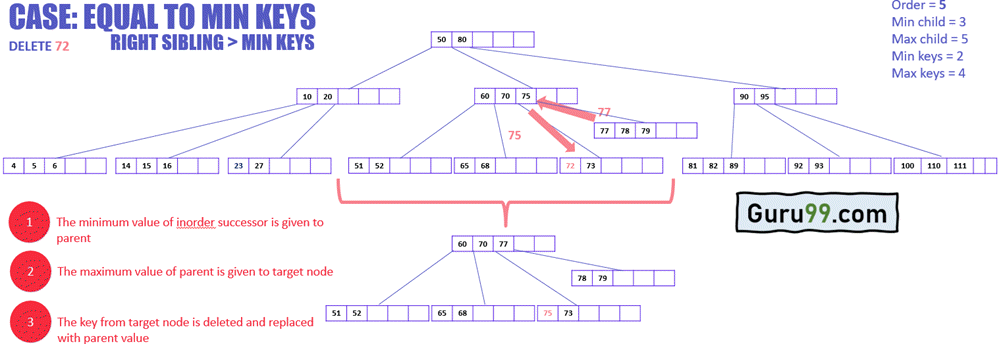
以下示例说明了如何删除需要从其中序后继借值的键。

Delete Operation

  • 目标节点将从其紧邻的兄弟节点借用一个键，在这种情况下，中序后继（右兄弟节点），因为它从中序前驱（左兄弟节点）借用的键数等于最小值。
  • 中序后继的最小值将转移到父节点，父节点将最大值转移到目标节点。

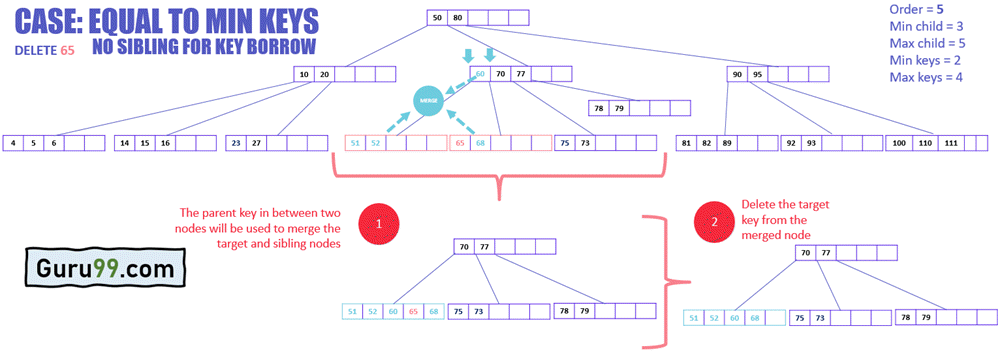
在下面的示例中，目标节点没有可以将其键提供给目标节点的兄弟节点。因此，需要合并。

相关文章

查看删除此类键的过程

Delete Operation

  • 将目标节点与任何一个紧邻的兄弟节点以及父键合并
  • 从父节点中选择位于两个合并节点之间的键
  • 从合并后的节点中删除目标键

删除操作伪代码

private int removeBiggestElement()
{
    if (root has no child)
        remove and return the last element
    else {
        answer = subset[childCount-1].removeBiggestElement()
        if (subset[childCount-1].dataCount < MINIMUM)
            fixShort (childCount-1)
        return answer
    }
}

输出:

B 树中删除了最大的元素。

摘要

  • B 树是一种自平衡数据结构，用于更好地从磁盘搜索、插入和删除数据。
  • B 树由指定的阶数进行调节
  • B 树的键和节点按升序排列。
  • B 树的搜索操作是最简单的，它总是从根开始，然后检查目标键是大于还是小于节点的值。
  • B 树的插入操作相当详细，它首先找到目标键的合适插入位置，插入它，根据不同情况评估 B 树的有效性，然后相应地重构 B 树节点。
  • B 树的删除操作首先搜索要删除的目标键，删除它，然后根据目标节点、兄弟节点和父节点的最小/最大键数等多个情况评估有效性。