迪杰斯特拉算法:C++、Python 代码示例
什么是最短路径或最短距离?
从源顶点到目标顶点的成本最低的路径就是最短路径或最短距离。在图论中,可能存在从一个源到另一个目标的多个路由。在这些路由之间,如果存在一条成本最低的路由,我们就可以称之为最短路径算法。
这里的“成本”是指路由中的节点数或每个路径的成本总和。一条路径可以有一个或多个边。两个顶点之间的连接称为“边”。有各种类型的最短路径算法,例如 Dijkstra 算法、Bellman-Ford 算法等。
在这里,我们讨论 Dijkstra 算法
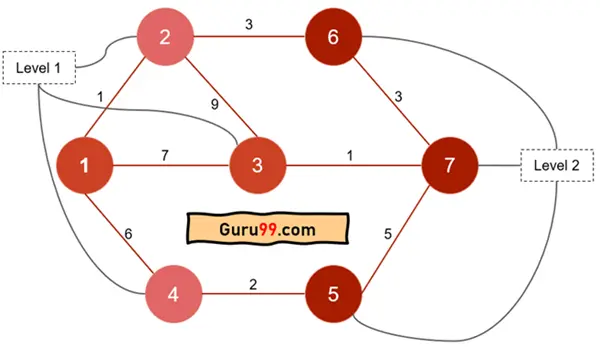
让我们看一下以下带权图
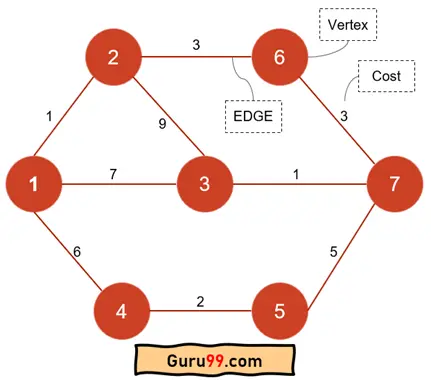
- “加权”一词意味着从一个节点移动到另一个节点的成本。例如,从节点 1 移动到节点 2,成本或权重为 1。
- 节点 1 到节点 2 之间的路径称为边。
- “无向”意味着您可以从一个节点移动到另一个节点,然后再返回到前一个节点。因此,如果我们尝试找到从节点 1 到节点 7 的所有路由,那么它将是
| 路线或路径 | 费用 |
|---|---|
| 1-2-6-7 | (1+3+3) = 7 |
| 1-2-3-7 | (1+9+1) = 11 |
| 1-3-7 | (7+1) = 8 |
| 1-4-5-7 | (6+2+5) = 13 |
在这四条路线中,我们可以看到第一条路线的成本为 7。因此,就成本而言,它是最短路径。
Dijkstra 算法如何工作
Dijkstra 算法可以找到有向和无向加权图中两点的最短距离。该算法是贪婪的,因为它总是选择离原点最近或最短的节点。“贪婪”一词意味着在一组结果或结果中,算法将选择其中最好的。
在这里,我们试图在所有其他路由中找到最短路径。因此,Dijkstra 算法找到从单个目标节点的所有最短路径。因此,它的行为类似于贪婪算法。
在下面的“示例”部分,您将看到逐步方法。它的工作原理如下
步骤 1) 将起始节点初始化为 0 成本,其余节点初始化为无穷大成本。
步骤 2) 维护一个数组或列表来跟踪已访问的节点
步骤 3) 使用最小成本更新节点成本。这可以通过比较当前成本与路径成本来完成。(示例部分显示了演示)
步骤 4) 继续步骤 3,直到所有节点都被访问。
完成所有这些步骤后,我们将找到从源到目标的成本最低的路径。
Dijkstra 与 BFS、DFS 的区别
Dijkstra 与 BFS-DFS 的主要区别在于 Dijkstra 是最短路径查找算法,而 BFS、DFS 是路径查找算法。在一般情况下,BFS 和 DFS 在查找路径时不会考虑成本。因此,这些算法不能保证最短路径。
BFS 如何工作的二维网格演示

此演示表明 BFS 只查找路径。但是,它不关心路径的权重。BFS(广度优先搜索)假设从一个节点到另一个节点的旅行成本仅为 1。
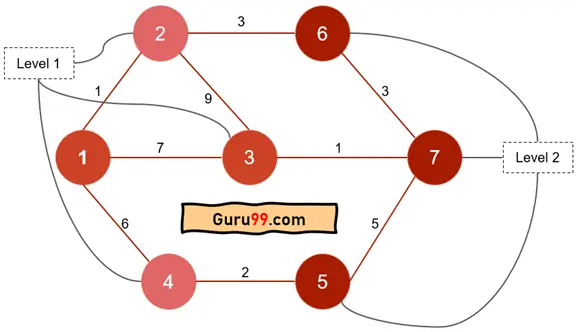
但是,让我们看一个示例图
这里,它找到了第 2 层的路径。BFS 按级别顺序遍历图。因此,它的遍历方式是
步骤 1) 从节点“1”开始,访问所有相邻节点 2、3、4
步骤 2) 将节点 2、3、4 标记为第 1 级,并访问它们的相邻节点。它将继续探索所有相邻节点,直到到达目标节点。
就 DFS 而言,它将按以下方式遍历从 1 到 7 的路径
- 1→2→3→7(原始成本 10,DFS 成本 3)
- 1→2→6→7(原始成本 7,DFS 成本 3)
- 1→3→7(原始成本 8,DFS 成本 2)
- 1→4→5→7(原始成本 13,DFS 成本 3)
正如我们所见,DFS 计算其路径成本是基于深度或边的数量。
DFS 执行以下操作
- DFS 可以找到从源(起始顶点)到目标节点的路径。
- 它不能保证从源节点到目标节点的路径是“最短路径”。
然而,就 Dijkstra 算法而言,它将根据边的成本来选择边。作为一种贪婪算法,它将选择最佳或最小成本的路径。
Dijkstra 算法示例
Dijkstra 算法使用成本或权重来计算路径的总成本。
Dijkstra 算法的目标是最小化此总成本或权重。在上面显示的示例中,我们找到从节点 1 到节点 7 的最佳路径,然后计算所有成本。
在 Dijkstra 算法中,它将通过计算权重来找到最短路径。它不会搜索所有可能的路径。让我们通过一个例子来演示 Dijkstra 算法。例如,您被要求找到从节点 1 到 7 的最短路径。
为此过程,步骤如下
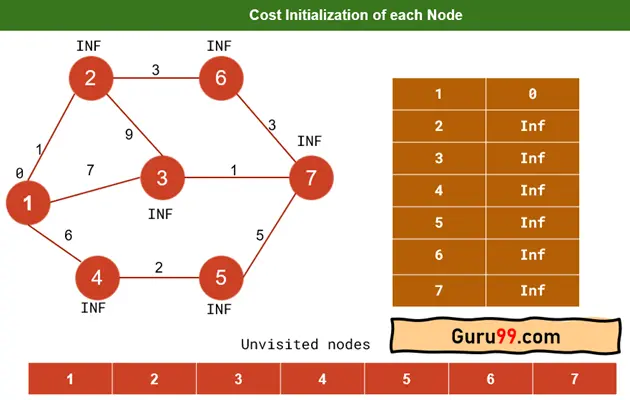
步骤 1) 将起始节点成本初始化为 0。
其余节点分配“Inf”。这意味着在起始顶点(源)和节点之间不存在路径,或者尚未访问该路径。
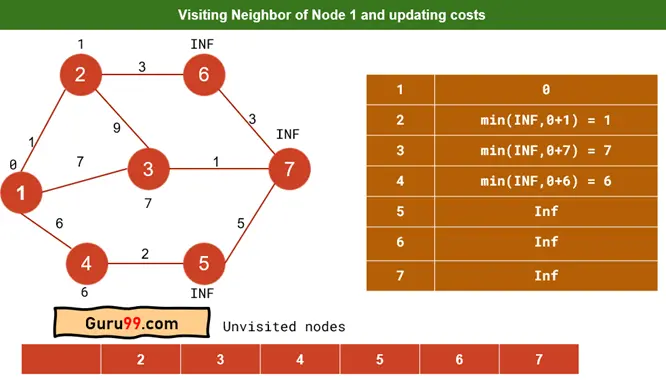
步骤 2) 当您选择节点 1 时,它将被标记为已访问。然后更新节点 1 的所有相邻邻居。2、3、4 是节点 1 的邻居节点。
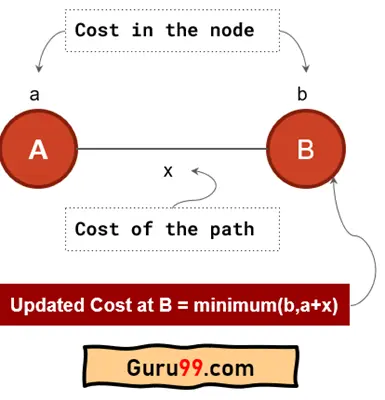
更新成本时,我们需要遵循以下过程
我们可以使用上述公式更新每个节点成本。例如,我们位于节点 1,需要更新其相邻节点 2、3、4 的成本。
更新后,成本或权重将如下所示
步骤 3) 对于节点“2”,邻居是 6 和 3。我们将通过比较无穷大(当前值)来更新“6”处的成本。节点 2 的成本 + 从 2 到 6 的路径成本。简单地说,节点“6”的成本将是 1+3 或 4。
节点 3 是节点 2 的邻居。但是,我们在上一步中计算了它的成本,为 7。现在,如果我们的路径是 1-2-3,节点 3 的成本将是 10。路径 1-2-3 的成本为 10,而 1 到 3 的成本为 7。
步骤 4) 对于节点 3,邻居节点是 7。因此,通过比较节点 7 的当前值与路径成本(7+1)或 8,我们将更新节点 7 的成本。即 8。
因此,我们找到了从节点 1 到节点 7 的路径,成本为 8。
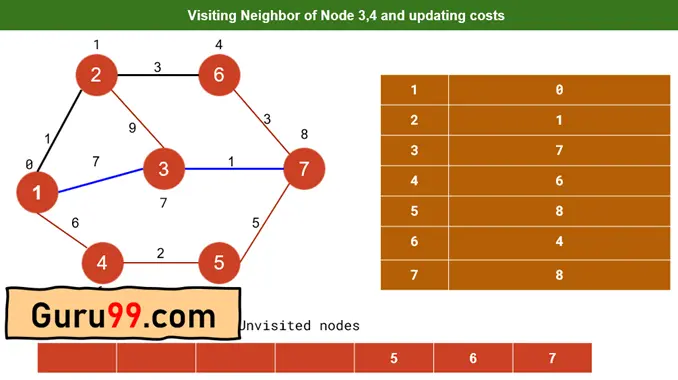
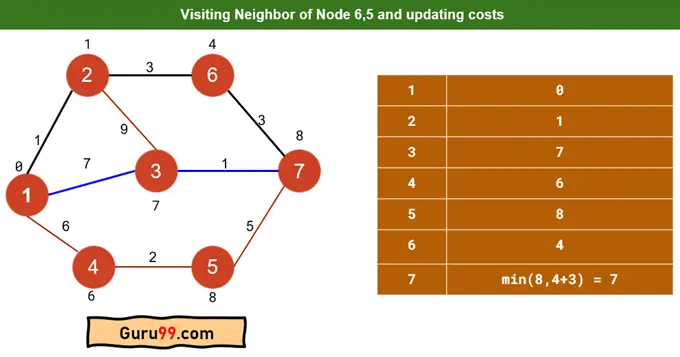
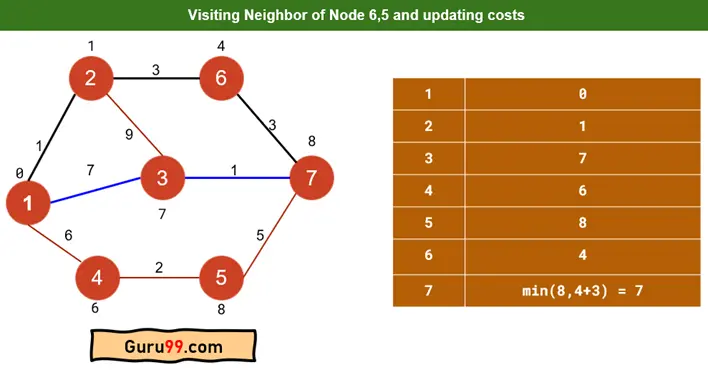
步骤 5) 对于节点 4,我们将相应地更新其相邻节点成本。因此,节点“5”的更新成本将为 8。完成步骤 4、5 后,它将如下所示
现在,路径 1-3-7 的成本为 8(先前)。节点“7”尚未标记为已访问,因为我们可以从节点“6”到达节点“7”。路径“1-2-6”的成本为 4。因此,路径 1-2-6-7 的成本为 7。
由于 7 < 8,因此从源顶点“1”到目标顶点“7”的最短路径将是 1-2-6-7,成本为 7。之前是 1-3-7,成本为 8。
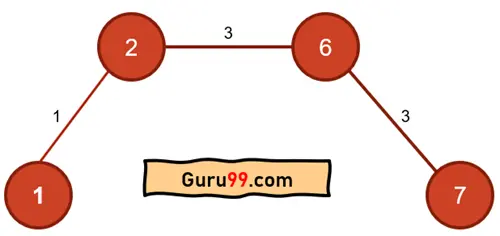
因此,最终图将如下所示
用黑线标记的边是我们从 1 到 7 的最短路径,成本为 7。
Dijkstra 算法的伪代码
这是 Dijkstra 算法的伪代码
Dijkstra(G, S):
for each vertex V in G
distance[V] & lt; - Infinity
previous[V] & lt; - NULL
if V does not equal S, then,
(priority queue) Q.push(V)
distance[S] = 0
While Q is not empty
U & lt; - Extract the MIN from Q
For each unvisited adjacent V of U
TotalDistance & lt; - distance[U] + edge_cost(U, V)
if TotalDistance is less than distance[V], then
distance[V] & lt; - TotalDistance
previous[V] & lt; - u
return distance, previous
Dijkstra 算法的 C++ 实现
要使用C++实现 Dijkstra 算法,代码如下
#include <bits/stdc++.h>
using namespace std;
#define size 7
int minimumDistance(int distance[], bool visited[]) {
int min = INT_MAX;
int min_index = INT_MAX;
for (int i = 0; i < size; i++) {
if (!visited[i] & amp; & distance[i] <= min) {
min = distance[i];
min_index = i;
}
}
return min_index;
}
void printParentPath(int parent[], int i) {
if (parent[i] == -1) {
return;
}
printParentPath(parent, parent[i]);
cout << i + 1 << " ";
}
void dijkstra(int graph[size][size], int source) {
int distance[size];
bool visited[size];
int parent[size];
for (int i = 0; i < size; i++) {
parent[0] = -1;
distance[i] = INT_MAX;
visited[i] = false;
}
distance[source] = 0;
for (int i = 0; i < size - 1; i++) {
int U = minimumDistance(distance, visited);
visited[U] = true;
for (int j = 0; j < size; j++) {
int curr_distance = distance[U] + graph[U][j];
if (!visited[j] & amp; & graph[U][j] & amp; &
curr_distance < distance[j]) {
parent[j] = U;
distance[j] = curr_distance;
}
}
}
cout << "Vertex\t\tDistance\tPath" << endl;
for (int i = 1; i < size; i++) {
cout << source + 1 << "->" << i + 1 << "\t\t" << distance[i] << "\t\t"
<< source + 1 << " ";
printParentPath(parent, i);
cout << endl;
}
}
int main() {
int graph[size][size] = {{0, 1, 7, 6, 0, 0, 0}, {1, 0, 9, 0, 0, 3, 0},
{7, 9, 0, 0, 0, 0, 1}, {6, 0, 0, 0, 2, 0, 0},
{0, 0, 0, 2, 0, 0, 0}, {0, 3, 0, 0, 0, 0, 3},
{0, 0, 0, 0, 5, 3, 0}};
dijkstra(graph, 0);
}
输出
Vertex Distance Path 1->2 1 1 2 1->3 7 1 3 1->4 6 1 4 1->5 8 1 4 5 1->6 4 1 2 6 1->7 7 1 2 6 7
Dijkstra 算法的 Python 实现
要使用Python实现 Dijkstra 算法,代码如下
num_of_vertex = 7
def minimumDistance(distance, visited):
_min = 1e11
min_index = 1e11
for i in range(num_of_vertex):
if not visited[i] and distance[i] & lt; = _min:
_min = distance[i]
min_index = i
return min_index
def printParentNode(parent, i):
if parent[i] == -1:
return
printParentNode(parent, parent[i])
print("{} ".format(i + 1), end = "")
def dijkstra(graph, src):
distance = list()
visited = list()
parent = list()
for i in range(num_of_vertex):
parent.append(-1)
distance.append(1e11)
visited.append(False)
distance[src] = 0
for i in range(num_of_vertex - 1):
U = minimumDistance(distance, visited)
visited[U] = True
for j in range(num_of_vertex):
curr_distance = distance[U] + graph[U][j]
if not visited[j] and graph[U][j] and curr_distance & lt;
distance[j]: parent[j] = U
distance[j] = curr_distance
print("Vertex\t\tDistance\tPath")
for i in range(num_of_vertex):
print("{}->{}\t\t{}\t\t{}
".format(src + 1, i + 1, distance[i], src + 1), end = "")
printParentNode(parent, i)
print("")
graph = [
[0, 1, 7, 6, 0, 0, 0],
[1, 0, 9, 0, 0, 3, 0],
[7, 9, 0, 0, 0, 0, 1],
[6, 0, 0, 0, 2, 0, 0],
[0, 0, 0, 2, 0, 0, 0],
[0, 3, 0, 0, 0, 0, 3],
[0, 0, 0, 0, 5, 3, 0]
]
dijkstra(graph, 0)
输出
Vertex Distance Path 1->1 0 1 1->2 1 1 2 1->3 7 1 3 1->4 6 1 4 1->5 8 1 4 5 1->6 4 1 2 6 1->7 7 1 2 6 7
我们可以看到该算法计算了从源节点到目标节点的最短距离。
Dijkstra 算法的应用
Dijkstra 算法有大量的用途。其中,它广泛应用于网络领域。以下是 Dijkstra 算法的一些实际应用
Google Maps 中的 Dijkstra:基本上,该算法是查找最短路径的支柱。正如我们从上面的代码片段输出中看到的。
Google 不使用简单的 Dijkstra 算法。相反,它使用修改后的版本。当您选择目的地时,它会在 Google 地图中显示多个路径。在这些路径中, some paths are sorted out for the user. These selected paths are based on "time". So, "time" is an edge cost for the shortest path.
IP 路由中的 Dijkstra:IP 路由是网络术语。它指的是数据包如何通过不同的路径发送到接收者。这些路径由路由器、服务器等组成。在 IP 路由中,有不同类型的协议。
这些协议帮助路由器找到发送数据的最短路径。其中一种协议的名称是“OSPF(开放最短路径优先)”。OSPF 使用 Dijkstra 算法。路由器维护一个路由表。每个路由器与其邻居路由器共享其表。在收到更新的表后,它们必须重新计算所有路径。那时,路由器使用 Dijkstra 算法。
Dijkstra 算法的局限性
Dijkstra 算法不能保证在负边图中的最短路径。Dijkstra 算法遵循以下方法
- 从一个节点到另一个节点将采取一条最短路径。
- 一旦选择了两个节点之间的最短路径,它就不会被再次计算。
在此,请注意两个带有负边的示例。
在左侧的图中,有三个顶点。Dijkstra 将像以下方式在图中运行
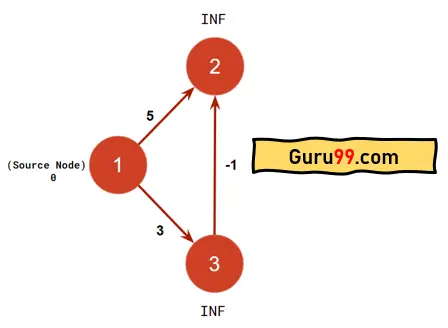
步骤 1) 起始顶点“1”将被初始化为零。其他节点将具有无穷大。
步骤 2) 将节点“1”标记为已访问并包含在最短路径中。
步骤 3) 源节点 1 到节点“2”和“3”的距离设置为无穷大,因为最短路径尚未计算。因此,任何成本小于无穷大的路径都将添加到最短路径(贪婪方法)中。
步骤 4) 更新从源顶点或源节点“1”到“2”的距离。当前权重将为 5(5 < 无穷大)。类似地,将节点“1”到“3”的距离更新为权重 3。
步骤 5) 现在,如果我们检查从节点“1”开始的最短距离,我们会发现 5 是边 1->2 的最短距离。因此,节点“2”将被标记为已访问。
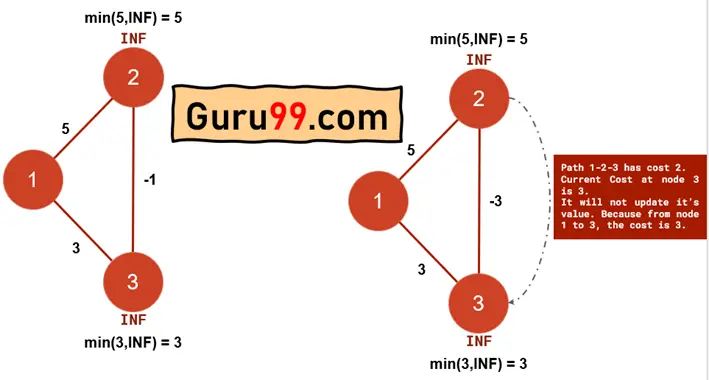
类似地,节点“3”也将被标记为已访问,因为最短距离是 3。
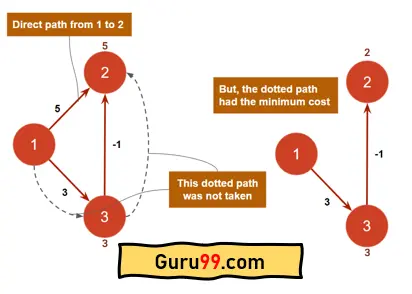
但是,如果我们观察,有一条路径 1-3-2 的成本仅为 2。但 Dijkstra 显示从节点“1”到节点“2”的最短距离是 5。因此,Dijkstra 未能正确计算最短距离。发生这种情况的原因是,Dijkstra 是一种贪婪算法。因此,一旦节点被标记为已访问,它就不会被重新考虑,即使可能存在更短的路径。此问题仅在边具有负成本或负权重边时发生。
Dijkstra 在这种情况下未能计算两个节点之间的最短路径。因此,该算法存在一些缺点。为了解决这个负边问题,使用了另一种称为“Bellman-Ford 算法”的算法。该算法可以处理负边。
Dijkstra 算法的复杂度
上述实现使用了两个“for”循环。这些循环运行的次数等于顶点数。因此,时间复杂度为O(V2)。此处,“0”表示对 Dijkstra 算法进行假设的符号。
我们可以使用“优先队列”来存储图。优先队列是二叉堆数据结构。它比二维矩阵更有效。具有最小成本的边将具有更高的优先级。
那么时间复杂度将是O(E log(V))。这里,E 是边的数量,V 是顶点的数量。
空间复杂度为O(V2),因为我们使用的是邻接矩阵(二维数组)。使用邻接列表或队列数据结构可以优化空间复杂度。