双向链表:C++、Python(代码示例)
什么是双向链表?
在双向链表中,每个节点都包含指向前一个节点和后一个节点的链接。每个节点包含三个元素:一个存储数据,另外两个是指向下一个和上一个节点的指针。这两个指针帮助我们从某个节点向前或向后移动。
这是双向链表的基本结构。
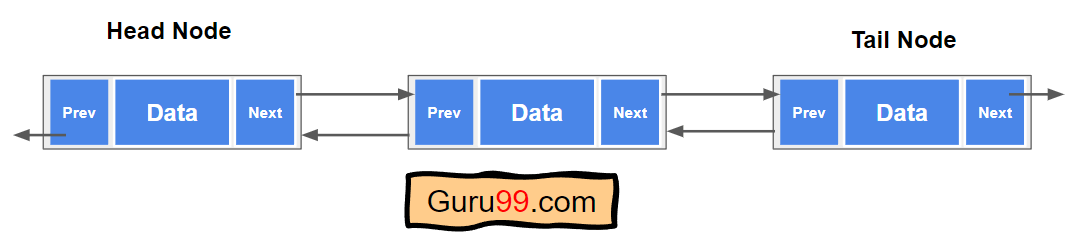
每个链表都有一个头节点和一个尾节点。头节点没有“prev”(前驱指针)节点,尾节点没有“next”节点。
以下是双向链表的一些重要术语
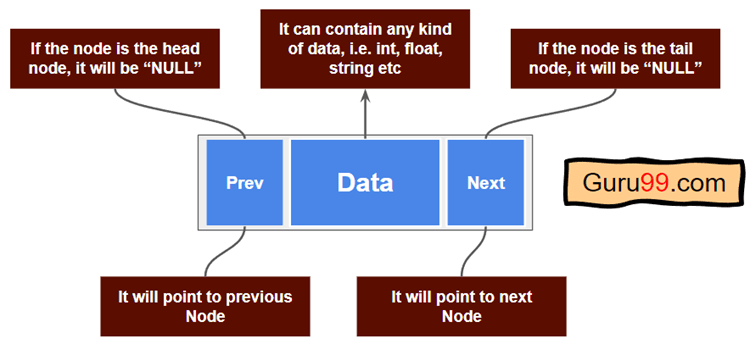
- Prev:每个节点都链接到其前一个节点。它用作指针或链接。
- Next:每个节点都链接到其后一个节点。它用作指针或链接。
- Data:用于在节点中存储数据。“Data”可以包含其他数据结构。例如,“Data”中可以存储字符串、字典、集合、哈希表等。
这是双向链表中单个节点的基本结构
双向链表的操作
双向链表的操作包括添加和删除节点、插入和移除节点,以及从上到下遍历链表。
以下是我们可以使用双向链表实现的操作列表
- 前端插入
- 尾部或最后一个节点插入
- 在节点后插入
- 在节点前插入
- 从前端删除
- 从尾部删除
- 搜索并删除节点
- 从头到尾遍历
- 从尾到头遍历
我们将看到上述所有操作的实现和伪代码。
在双向链表前端插入
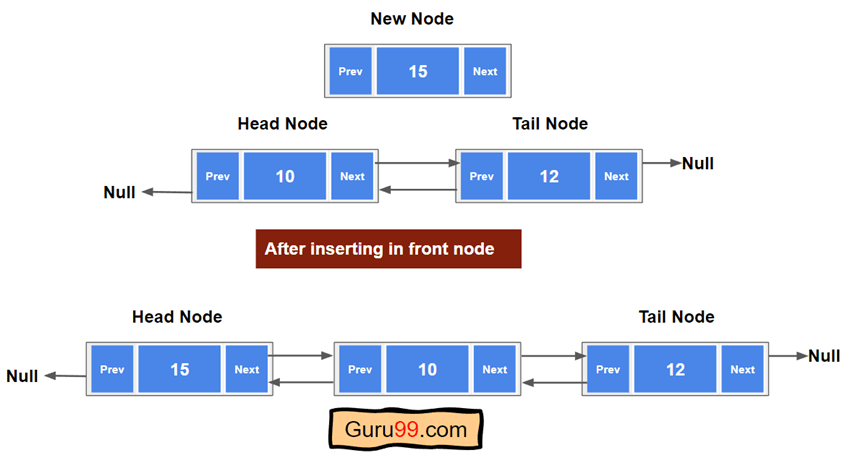
前端插入意味着我们需要在链表中创建一个节点并将其放置在链表的开头。
例如,有一个给定的节点“15”。我们需要将其添加到头节点。
在此操作中有两个重要条件
- 如果双向链表中没有节点,新节点将成为头节点。
- 如果已经存在头节点,新节点将替换前一个头节点。
这是此操作的伪代码
function insertAtFront (ListHead, value): newNode = Node() newNode.value = value ListHead.prev = NewNode NewNode.next = ListHead newNode.prev = NULL return ListHead
在双向链表末尾插入
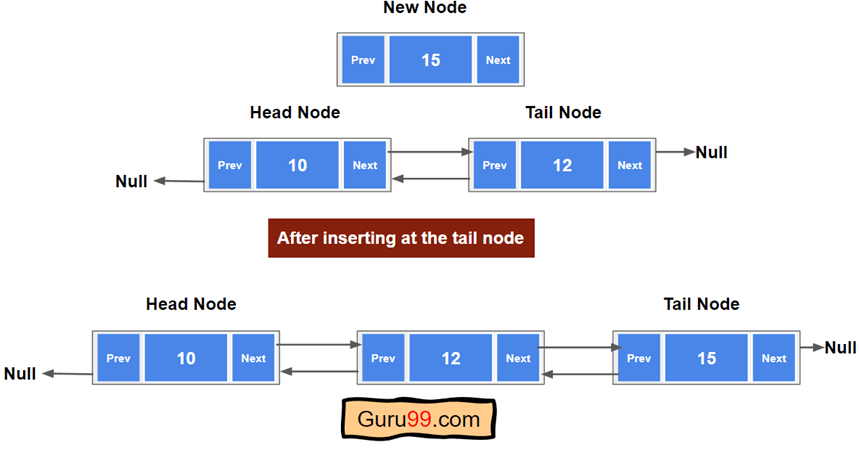
“末尾插入”意味着我们将创建一个链表节点并将其放置在末尾。
要执行此操作,我们可以使用两种方法
- 方法 1:从双向链表的头部开始遍历,直到“next”变为 null。然后将新节点与“next”链接。
- 方法 2:获取双向链表的最后一个节点。然后,最后一个节点的“next”节点将链接到新节点。现在,新节点将成为尾节点。
这是在尾节点插入的伪代码
function insertAtTail(ListHead, value): newNode = Node() newNode.value = value newNode.next = NULL while ListHead.next is not NULL: then ListHead = ListHead.next newNode.prev = ListHead ListHead.next = newNode return ListHead
在节点后插入
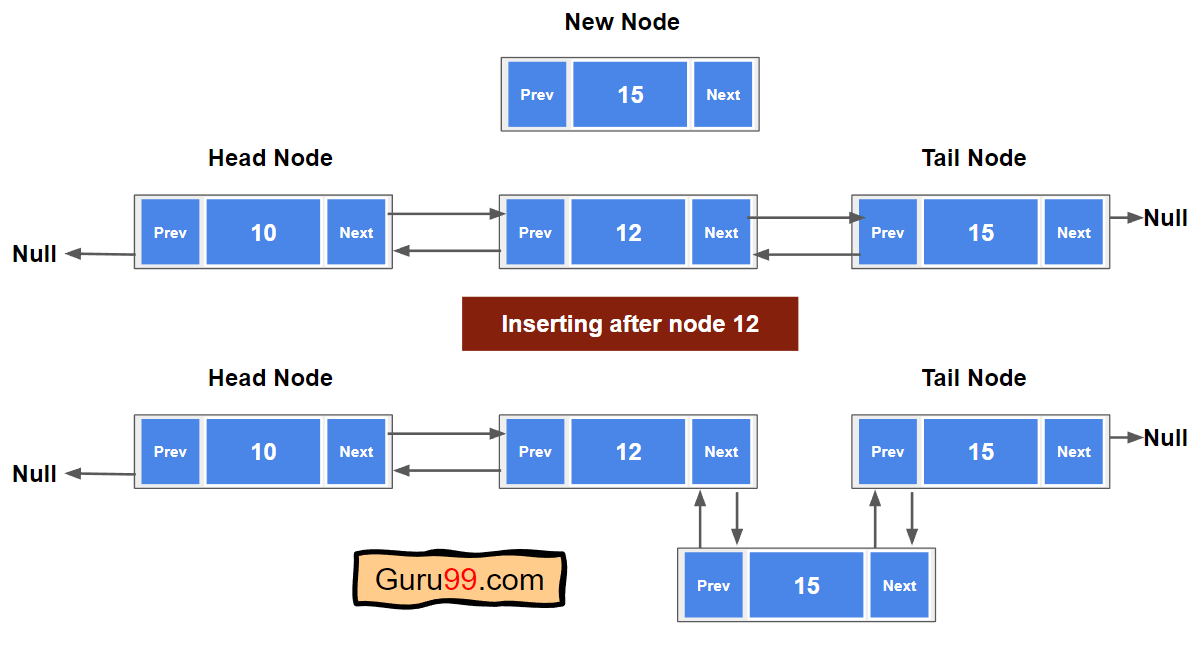
假设我们有一个如下的双向链表
我们想插入一个给定节点,该节点将链接到值为“12”的节点之后。
以下是执行此操作的步骤
步骤 1)从头部遍历到最后一个节点。检查哪个节点的值为“12”。
步骤 2)创建一个新节点,并将其指定为节点“12”的下一个指针。新节点的“next”节点将是 15。
这是在双向链表中在节点后插入节点的伪代码
function insertAfter(ListHead, searchItem, value): List = ListHead NewNode = Node() NewNode.value = value while List.value is not equal searchItem then List = ListHead.next List = List.next NewNode.next = List.next NewNode.prev = List List.next = NewNode
在节点前插入
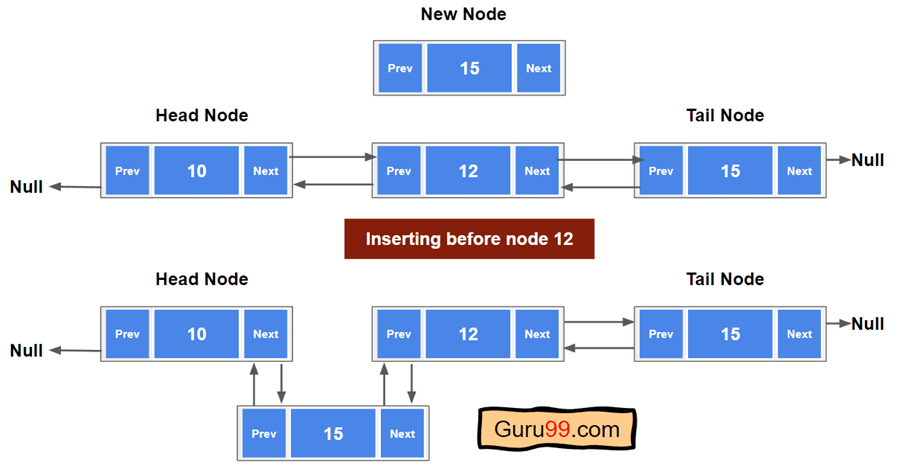
此操作与“在节点后插入”类似。我们需要搜索特定节点的值来执行此操作。然后,我们将创建一个新节点并将其插入到搜索到的节点之前。
假设我们想在节点“12”之前插入一个给定节点“15”。那么执行此操作的步骤如下
步骤 1)从头节点遍历链表到尾节点。
步骤 2)检查当前节点的下一个指针是否值为“12”。
步骤 3)将新节点插入为当前节点的“next”节点。
这是在双向链表中在节点前插入节点的伪代码
function insertBefore(ListHead, searchItem, value): List = ListHead NewNode = Node() NewNode.value = value while List.next.value is not equal searchItem then List = ListHead.next NewNode.next = List.next NewNode.prev = List List.next = NewNode
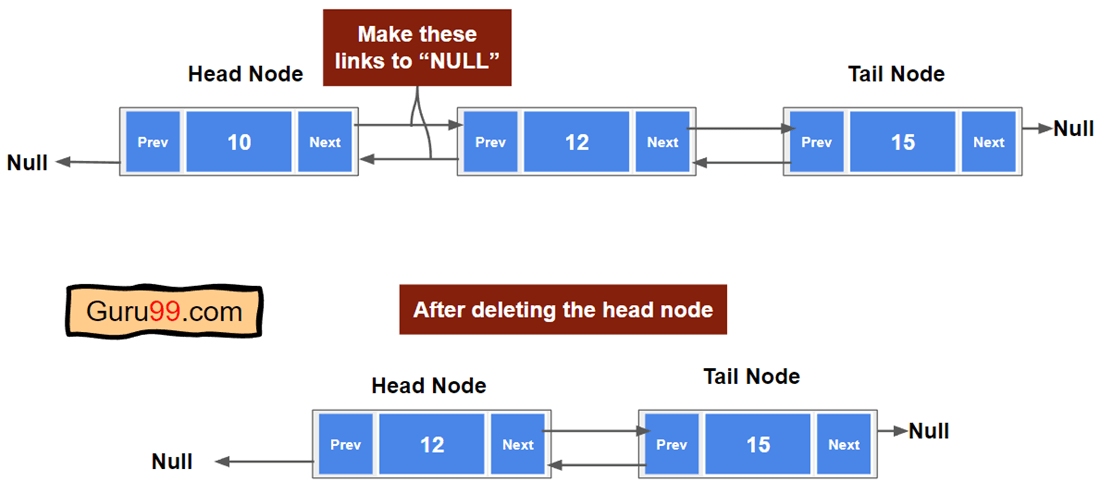
删除双向链表的头节点
双向链表中的头节点没有前驱节点。因此,如果要删除头节点,则下一个指针将成为新的头节点。删除节点时,我们还需要释放节点占用的内存。
以下是删除头节点的步骤
步骤 1)将一个变量分配给当前头节点。
步骤 2)访问当前头节点的“next”节点,并将“prev”(前驱指针)节点设置为“NULL”。这意味着我们正在断开第二个节点与第一个节点的连接。
步骤 3)释放前一个头节点占用的内存。
这是从双向链表中删除头节点的伪代码
function deleteHead(ListHead): PrevHead = ListHead ListHead = ListHead.next ListHead.prev = NULL PrevHead.next = NULL free memory(PrevHead) return ListHead
在执行任何删除操作后,必须删除已分配的内存。否则,在程序的整个运行期间,已删除块的内存将一直被占用。任何其他应用程序都无法使用该内存段。
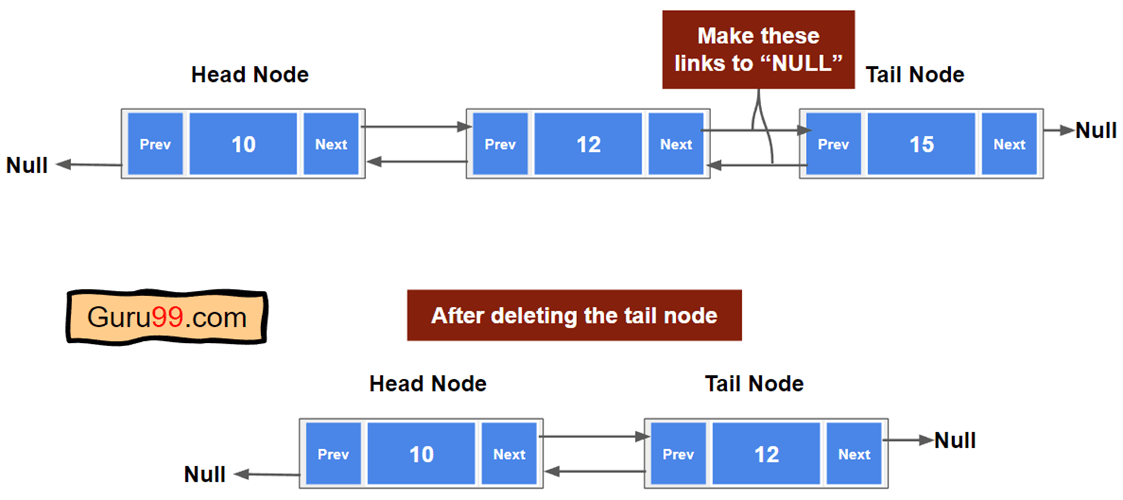
删除双向链表的尾节点。
此操作与删除头节点类似。这里,我们需要删除尾节点而不是头节点。要将节点识别为尾节点,我们应检查下一个指针或下一个节点是否为 null。删除尾节点后,我们需要释放内存。
此操作也称为“从末尾删除”。
以下是执行此操作的步骤
步骤 1)遍历直到到达双向链表的尾节点。
步骤 2)将一个变量或指针分配给尾节点。
步骤 3)将“next”节点设置为 NULL 并释放尾节点的内存。
这是删除尾节点的伪代码
function DeleteTail( ListHead ): head = ListHead while ListHead.next is not NULL: ListHead = ListHead.next Tail = ListHead.next ListHead.next = NULL free memory( Tail ) return head
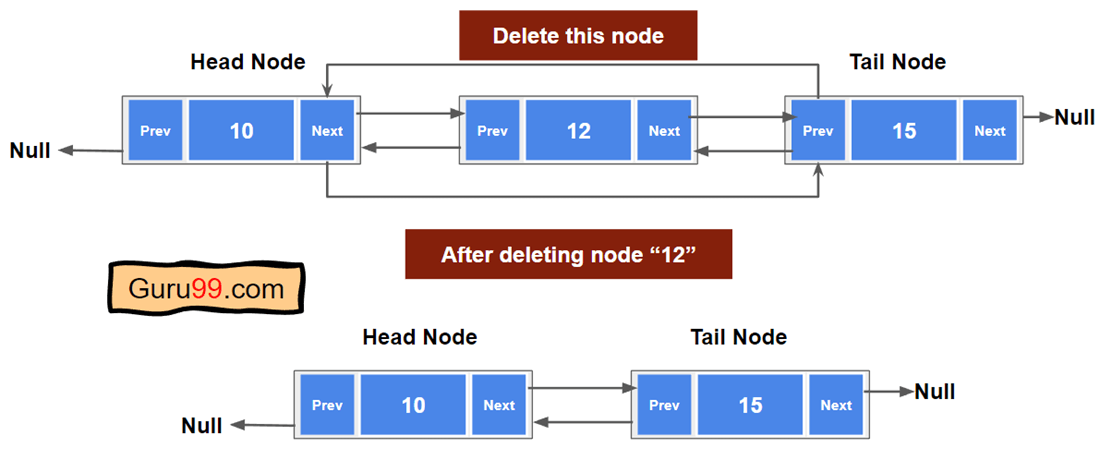
从双向链表中搜索并删除节点
此操作允许我们搜索特定节点数据并删除该节点。由于链表是线性数据结构,因此我们需要执行线性搜索。删除后,我们还需要释放内存。
以下是在双向链表中搜索并删除节点的步骤
步骤 1)从头遍历链表,直到节点的值等于搜索项。
步骤 2)将变量“deleteNode”分配给匹配的节点。
步骤 3)将“deleteNode”的前一个节点分配给下一个节点。
步骤 4)释放“deleteNode”的内存
这是从链表中搜索并删除节点的伪代码
function SearchAndDelete(ListHead, searchItem): head = ListHead while ListHead.next.value not equals searchItem: head = head.next deleteNode = head.next head.next = head.next.next head.next.prev = head deleteNode.next, deleteNode.next = NULL free memory(deleteNode) return ListHead
从前向遍历双向链表
从头节点遍历并迭代下一个节点,直到找到“NULL”。在遍历每个节点时,我们可以打印节点的值。以下是从前端(正向)遍历的步骤
步骤 1)将指针或变量分配给当前头节点。
步骤 2)迭代到头节点的下一个节点,直到遇到“NULL”
步骤 3)在每次迭代中打印节点数据。
步骤 4)返回头节点。
这是从前端遍历双向链表的伪代码
function traverseFromFront(ListHead): head = ListHead while head not equals to NULL: print head.data head = head.next return ListHead
这里,返回不是强制性的。但操作后返回头节点是一个好习惯。
从后向前遍历双向链表
此操作是从前端遍历的逆操作。方法相同,但略有不同。我们必须遍历到尾节点,然后从尾节点遍历到前节点。
以下是从后端遍历双向链表的步骤
步骤 1)遍历直到到达尾节点。
步骤 2)从尾节点开始,我们将遍历直到前一个节点变为“NULL”。头节点的前驱指针(“prev”)为 null。
步骤 3)在每次迭代中,我们将打印节点数据。
这是从后端遍历的伪代码
function traverseFromBack(ListHead): head = ListHead while head not equals NULL: head = head.next tail = head while tail not equal to NULL: print tail.value tail = tail.prev return ListHead
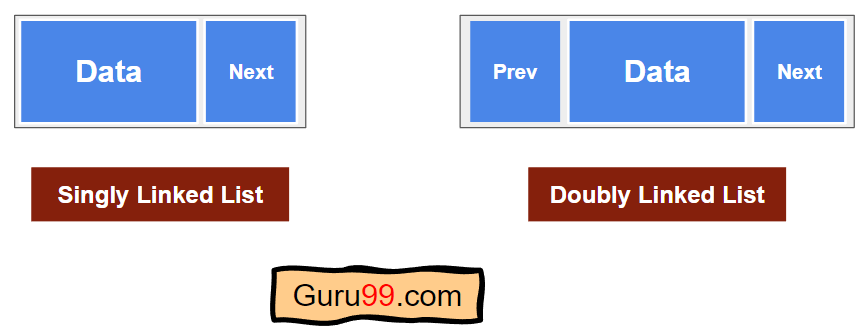
单向链表与双向链表的区别
单向链表与双向链表的主要区别在于链接的数量。
以下是单向链表节点与双向链表节点结构之间的区别
| 字段 | 单向链表 | 双向链表 |
|---|---|---|
| 结构体 | 单向链表只有一个数据字段和一个指向下一个节点的链接。 | 双向链表有一个数据字段和两个链接。一个指向前一个节点,另一个指向后一个节点。 |
| 遍历 | 只能从头到尾遍历。 | 可以向前和向后遍历。 |
| 内存 | 占用内存较少。 | 它比单向链表占用更多内存。 |
| 可访问性 | 单向链表效率较低,因为它们只使用一个链接指向下一个节点。没有指向前一个节点的链接。 | 双向链表比单向链表效率更高。 |
C++ 中的双向链表
#include<iostream>
using namespace std;
struct node{
int data;
struct node *next;
struct node *prev;
};
void insertFront(node* &listHead, int value){
node* newNode = new node();
newNode->data = value;
newNode->prev = NULL;
newNode->next = NULL;
if(listHead!=NULL)
{
listHead->prev = newNode;
newNode->next = listHead;
}
listHead = newNode;
cout<<"Added "<<value<<" at the front"<<endl;
}
void insertEnd(node * &listHead, int value){
if(listHead==NULL)
{
insertFront(listHead,value);
}
node* newNode = new node();
newNode->data = value;
newNode->prev = NULL;
newNode->next = NULL;
node *head = listHead;
while(head->next!=NULL){
head = head->next;
}
head->next = newNode;
newNode->prev = head;
cout<<"Added "<<value<<" at the end"<<endl;
}
void insertAfter(node * &listHead, int searchValue,int value){
node* newNode = new node();
newNode->data = value;
newNode->prev = NULL;
newNode->next = NULL;
node *head = listHead;
while(head->next!=NULL && head->data!=searchValue){
head = head->next;
}
newNode->next = head->next;
head->next = newNode;
newNode->prev = head;
if(newNode->next !=NULL){
newNode->next->prev = newNode;
}
cout<<"Inserted "<<value<<" after node "<<searchValue<<endl;
}
void insertBefore(node * &listHead, int searchValue,int value){
node* newNode = new node();
newNode->data = value;
newNode->prev = NULL;
newNode->next = NULL;
node *head = listHead;
while(head->next!=NULL && head->next->data!=searchValue){
head = head->next;
}
newNode->next = head->next;
head->next = newNode;
newNode->prev = head;
if(newNode->next !=NULL){
newNode->next->prev = newNode;
}
cout<<"Inserted "<<value<<" before node "<<searchValue<<endl;
}
void traverseFromFront(node *listHead){
node* head = new node();
head = listHead;
cout<<"Traversal from head:\t";
while(head!=NULL){
cout<<head->data<<"\t ";
head = head->next;
}
cout<<endl;
}
void traverseFromEnd(node *listHead){
node* head = new node();
head = listHead;
cout<<"Traversal from head:\t";
while(head->next!=NULL){
head = head->next;
}
node *tail = head;
while(tail!=NULL){
cout<<tail->data<<"\t";
tail = tail->prev;
}
cout<<endl;
}
void searchAndDelete(node **listHead, int searchItem){
node* head = new node();
head = (*listHead);
while(head->next!=NULL && head->data!=searchItem){
head = head->next;
}
if(*listHead == NULL || head == NULL) return;
if((*listHead)->data == head->data){
*listHead = head->next;
}
if(head->next != NULL){
head->next->prev = head->prev;
}
if(head->prev != NULL){
head->prev->next = head->next;
}
free(head);
cout<<"Deleted Node\t"<<searchItem<<endl;
return;
}
int main(){
node *head = NULL;
insertFront(head,5);
insertFront(head,6);
insertFront(head,7);
insertEnd(head,9);
insertEnd(head,10);
insertAfter(head,5,11);
insertBefore(head,5,20);
traverseFromFront(head);
traverseFromEnd(head);
searchAndDelete(&head,7);
traverseFromFront(head);
traverseFromEnd(head);
}
输出
Added 5 at the front Added 6 at the front Added 7 at the front Aded 9 at the end Added 10 at the end Inserted 11 after node 5 Inserted 20 before node 5 Traversal from head: 7 6 20 5 11 9 10 Traversal from head: 10 9 11 5 20 6 7 Deleted Node 7 Traversal from head: 6 20 5 11 9 10 Traversal from head: 10 9 11 5 20 6
Python 中的双向链表
class node:
def __init__(self,data = None, prev=None, next = None):
self.data = data
self.next = next
self.prev = prev
class DoublyLinkedList:
def __init__(self):
self.head = None
def insertFront(self, val):
newNode = node(data=val)
newNode.next = self.head
if self.head is not None:
self.head.prev = newNode
self.head = newNode
print("Added {} at the front".format(val))
def insertEnd(self,val):
newNode = node(data=val)
if self.head is None:
self.insertFront(val)
temp = self.head
while temp.next is not None:
temp = temp.next
temp.next = newNode
newNode.prev = temp
print("Added {} at the end".format(val))
def traverseFromFront(self):
temp = self.head
print("Traversing from head:\t",end="")
while temp:
print("{}\t".format(temp.data),end="")
temp = temp.next
print()
def traverseFromEnd(self):
temp = self.head
print("Traversing from Tail:\t",end="")
while temp.next is not None:
temp = temp.next
tail = temp
while tail is not None:
print("{}\t".format(tail.data),end="")
tail = tail.prev
print()
def insertAfter(self,searchItem, value):
newNode = node(data=value)
temp = self.head
while temp.next is not None and temp.data is not searchItem:
temp = temp.next
newNode.next = temp.next
temp.next = newNode
newNode.prev = temp
if newNode.next is not None:
newNode.next.prev = newNode
print("Inserted {} after node {}".format(value,searchItem))
def insertBefore(self,searchItem, value):
newNode = node(data=value)
temp = self.head
while temp.next is not None and temp.next.data is not searchItem:
temp = temp.next
newNode.next = temp.next
temp.next = newNode
newNode.prev = temp
if newNode.next is not None:
newNode.next.prev = newNode
print("Inserted {} before node {}".format(value,searchItem))
def searchAndDelete(self,searchItem):
temp = self.head
while temp.next is not None and temp.data is not searchItem:
temp = temp.next
if self.head is None or temp is None:
return
if self.head.data is temp.data:
self.head = temp.next
if temp.next is not None:
temp.next.prev = temp.prev
if temp.prev is not None:
temp.prev.next = temp.next
print("Deleted Node\t{}".format(searchItem))
return
doublyLinkedList = DoublyLinkedList()
doublyLinkedList.insertFront(5)
doublyLinkedList.insertFront(6)
doublyLinkedList.insertFront(7)
doublyLinkedList.insertEnd(9)
doublyLinkedList.insertEnd(10)
doublyLinkedList.insertAfter(5, 11)
doublyLinkedList.insertBefore(5, 20)
doublyLinkedList.traverseFromFront()
doublyLinkedList.traverseFromEnd()
doublyLinkedList.searchAndDelete(7)
doublyLinkedList.traverseFromFront()
doublyLinkedList.traverseFromEnd()
输出
Added 5 at the front Added 6 at the front Added 7 at the front Added 9 at the end Added 10 at the end Inserted 11 after node 5 Inserted 20 before node 5 Traversing from head: 7 6 20 5 11 9 10 Traversing from Tail: 10 9 11 5 20 6 7 Deleted Node 7 Traversing from head: 6 20 5 11 9 10 Traversing from Tail: 10 9 11 5 20 6
双向链表的复杂度
通常,时间复杂度分为三种类型。
它们是
- 最佳情况
- 平均情况
- 最坏情况
双向链表的最佳情况下的时间复杂度
- 在头部或尾部插入的成本为 O(1)。因为我们不需要在链表中进行遍历。头部和尾部指针可以让我们以 O(1) 的时间复杂度访问头部和尾部节点。
- 在头部或尾部删除的成本为 O(1)。
- 搜索节点的时间复杂度为 O(1)。因为目标节点可以是头节点。
双向链表的平均情况下的时间复杂度
- 在头部或尾部插入的时间复杂度为 O(1)。
- 在头部或尾部删除的时间复杂度为 O(1)。
- 搜索节点的时间复杂度为 O(n)。因为搜索项可能位于链表中的任何位置。这里,“n”是链表中存在的节点总数。
双向链表的最坏情况时间复杂度将与平均情况相同。
双向链表的内存复杂度
内存复杂度为 O(n),其中“n”是节点总数。在实现链表时,我们必须释放使用的内存。否则,对于较大的链表,会导致内存泄漏。
摘要
- 链表是一种线性数据结构,是线性方式表示的数据集合。
- 双向链表是一种链表,其中一个节点同时具有指向前一个节点和后一个节点的链接。
- 双向链表包含所有操作,例如添加节点、删除节点、在另一个节点之后或之前插入节点,以及从头到尾遍历链表。
- 双向链表有一个数据字段和两个链接。一个指向前一个节点,另一个指向后一个节点。
- 双向链表的复杂度:最佳情况、平均情况
- 以及最坏情况。