数据结构中的单向链表
什么是单向链表?
单向链表是一种线性、单向的数据结构,数据保存在节点中,每个节点通过链接指向下一个节点。每个节点包含一个数据字段和一个指向下一个节点的链接。单向链表只能朝一个方向遍历,而双向链表可以朝两个方向遍历。
这是单向链表的节点结构
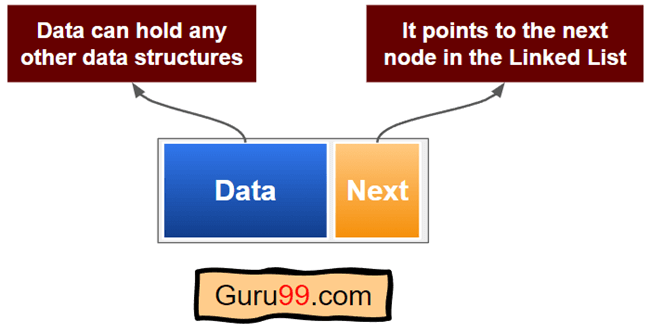
为什么用链表而不是数组?
在某些情况下,使用链表比使用数组更好。以下是一些场景
- 未知元素数量:当您在程序运行时不知道需要存储多少元素时,您可以使用链表。内存会在您向链表中添加元素时动态分配。
- 随机访问:在您不需要对元素进行随机访问的情况下,您可以使用链表。
- 在中间插入:在数组中间插入是一项复杂任务,因为您需要将其他元素向右推移。但是,链表允许您将元素添加到任何您想要的位置。
单向链表的操作
单向链表非常适合动态分配内存。它提供了链表的所有基本操作,即插入、删除、搜索、更新、合并两个链表、遍历等。
在这里,我们将讨论链表的以下操作
- 头部插入
- 尾部插入
- 在节点后插入
- 在节点前插入
- 删除头节点
- 删除尾节点
- 搜索和删除节点
- 遍历链表
这是一个具有四个节点的链表示例。
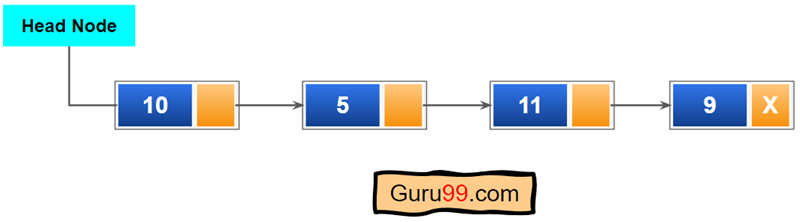
在单向链表的头部插入
这是一个简单的操作。通常,它被称为“压入”单向链表。您需要创建一个新节点并将其放置在链表的头部。
要执行此操作,我们需要遵循两个重要条件。它们是
- 如果列表为空,则新创建的节点将是头节点,头节点的下一个节点将是“NULL”。
- 如果列表不为空,新节点将是头节点,下一个将指向前一个头节点。
这是在链表头部插入节点的伪代码
function insertAtHead( head, value ): newNode = Node(value) if head is NULL: head = newNode return head else: newNode.next = head return newNode
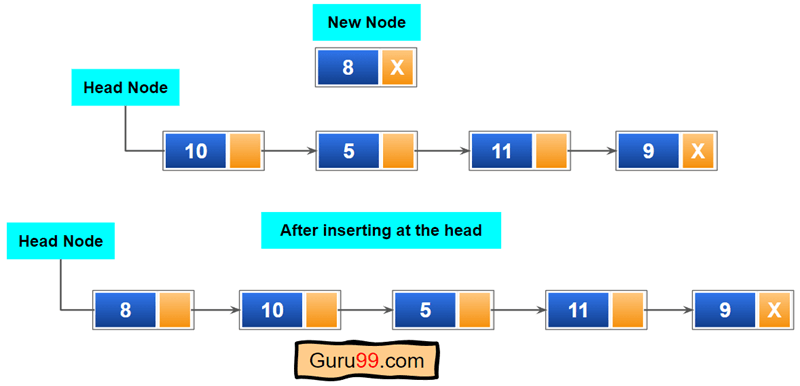
在单向链表的尾部插入
在链表末尾插入节点在某些方面与在头部插入相似。您需要做的就是遍历到最后一个节点或尾节点。然后将最后一个节点的“next”节点指向新创建的节点。如果头节点为 null,则新节点将是头节点。
以下是步骤
步骤 1) 遍历直到当前节点的“next”节点变为 null。
步骤 2) 创建一个具有指定值的新节点。
步骤 3) 将新节点指定为尾节点的下一个节点。
单向链表中在尾部插入节点的伪代码
function insertAtEnd( head, value ): newNode = Node(value) if head is NULL: head = newNode return head while head.next is not NULL: then head = head.next head.next = newNode newNode.next = NULL
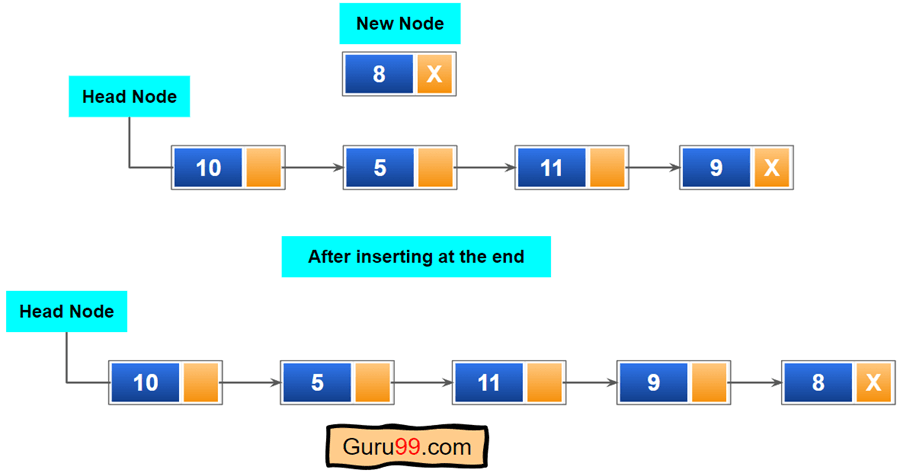
在节点后插入单向链表
在节点后插入包含两个部分:搜索节点并在找到的节点后附加。我们需要遍历所有节点。对于每个节点,我们需要将其与搜索的元素进行匹配。如果匹配,我们将新节点添加到搜索到的节点之后。
以下是步骤
步骤 1) 遍历下一个节点,直到当前节点的值等于搜索项。
步骤 2) 新节点的 next 指针将是当前节点的 next 指针。
步骤 3) 当前节点的 next 节点将是新节点。
这是在节点后插入节点的伪代码
function insertAfter( head, value, searchItem ): newNode = Node(value) while head.value equals searchItem: then head = head.next newNode.next = head.next.next head.next = newNode
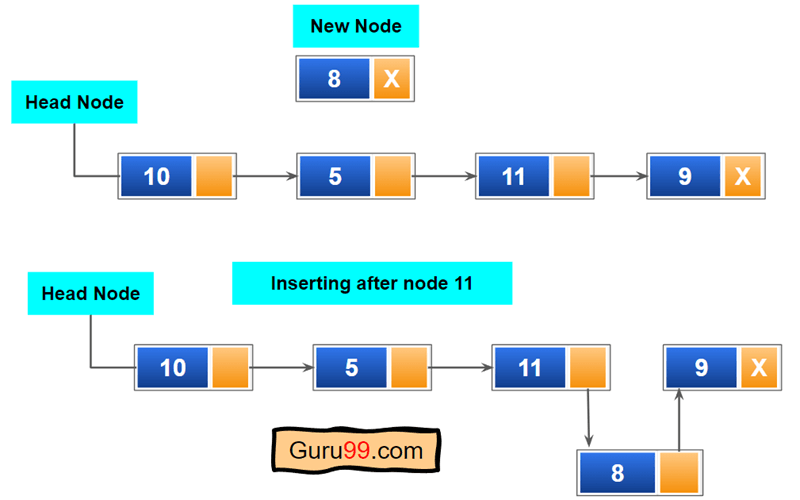
在节点前插入单向链表
此函数与在节点后插入非常相似。我们必须创建一个新节点并遍历链表,直到当前节点与搜索节点匹配。之后,我们将新节点添加为当前节点的前一个节点。
以下是步骤
步骤 1) 遍历直到下一个节点的值等于搜索项。
步骤 2) 创建一个新节点,并将节点的“next”指向当前节点的下一个节点。
步骤 3) 将新节点指定为当前节点的下一个节点。
这是伪代码
function insertBefore( head, value, searchItem ): newNode = Node(value) while head.next.value equals searchItem: then head = head.next newNode.next = head.next.next head.next = newNode
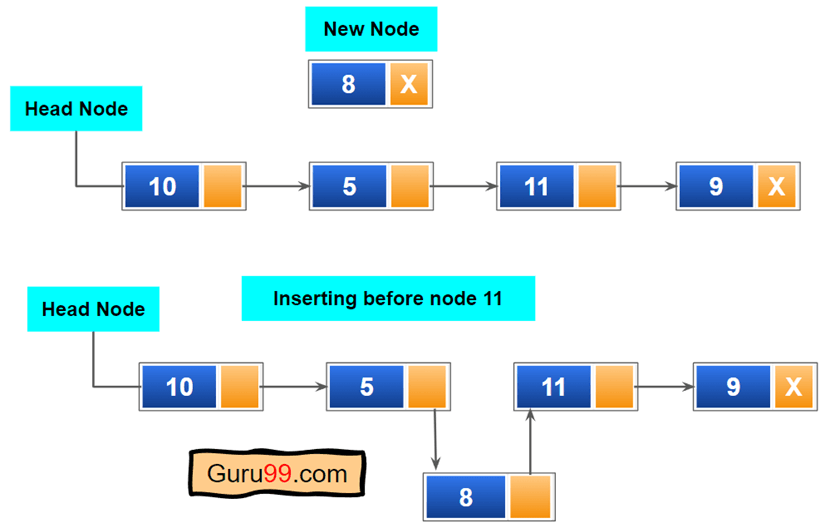
删除单向链表的头节点
在链表的每个函数中,都将头指针作为参数提供。您需要删除头节点,并将头节点的下一个节点设为链表的新头。我们还需要释放已删除节点占用的内存。否则,当另一个程序尝试访问它时,内存将被标记为已占用。
以下是删除单向链表头节点的步骤
步骤 1) 将头节点的下一个节点指定为新头。
步骤 2) 释放前一个头节点分配的内存。
步骤 3) 返回新的头节点。
删除头节点的伪代码
function deleteHead( head ): temp = head head = head.next free( temp ) return head
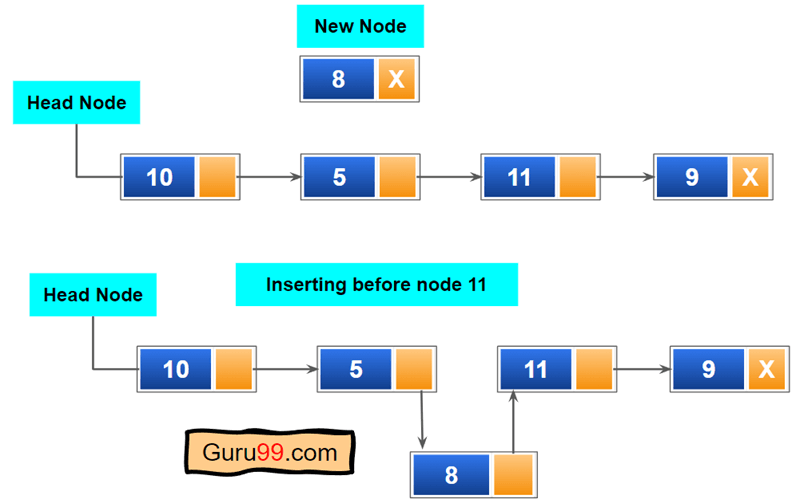
删除单向链表的尾节点
删除尾节点与删除头节点非常相似。区别在于我们需要遍历到链表的末尾并删除它。在单向链表中,next 节点为“NULL”的节点是尾节点。
以下是删除链表尾节点的步骤
步骤 1) 遍历到尾节点之前。保存当前节点。
步骤 2) 释放当前节点下一个节点的内存。
步骤 3) 将当前节点的下一个节点设置为 NULL。
这是删除尾节点的伪代码
function deleteTail( head ): while head.next.next is not NULL: head = head.next free( head.next ) head.next = NULL
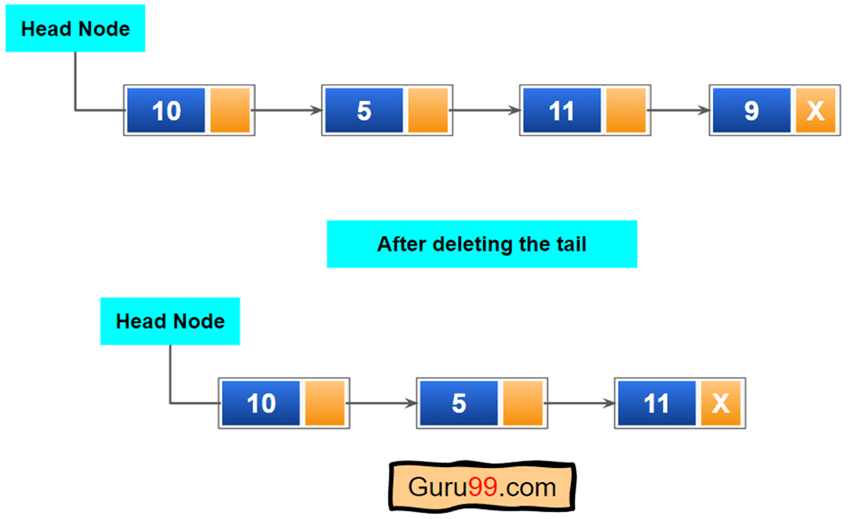
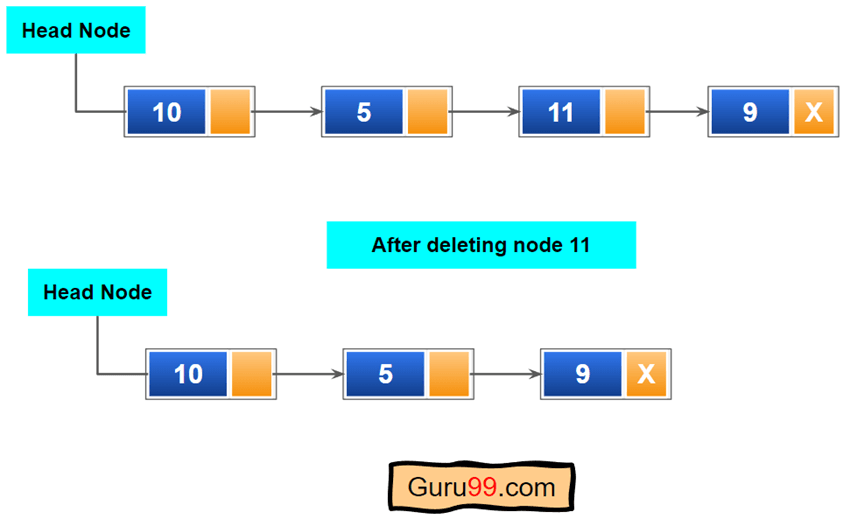
在单向链表中搜索并删除节点
此函数有两个任务:搜索和删除。我们需要搜索直到单向链表结束。如果我们找到任何匹配的节点,我们将删除它。之后,我们需要合并或链接已删除节点的左右节点。以下是执行此操作的步骤
步骤 1) 遍历到链表末尾。检查当前节点是否等于搜索节点。
步骤 2) 如果找到匹配的节点,请将节点指针存储到当前节点。
步骤 3) 前一个节点的“next”将是当前节点的下一个节点。
步骤 4) 删除并释放当前节点的内存。
从单向链表中搜索并删除节点的伪代码
function searchAndDelete( head, searchItem ): while head.next.next is not NULL and head.next.value is not equals searchItem : head = head.next head.next = head.next.next delete(head.next)
遍历单向链表
单向链表仅提供从头到尾的遍历功能。没有指向前一个节点的指针,因此我们无法反向遍历单向链表。我们将遍历每个节点并打印当前节点的值,直到遇到 null。
以下是步骤
步骤 1) 遍历每个节点,直到下一个节点为 null。
步骤 2) 打印当前节点的值。
遍历单向链表的伪代码
function traverse( head ): while head.next is not NULL: print the value of the head head = head.next
C++ 中的单向链表示例
#include<iostream>
using namespace std;
struct Node{
int data;
struct Node *next;
};
void insertAtHead(Node* &head, int value){
Node* newNode = new Node();
newNode->data = value;
newNode->next = NULL;
if(head!=NULL){
newNode->next = head;
}
head = newNode;
cout<<"Added "<<newNode->data<<" at the front"<<endl;
}
void insertEnd(Node* &head, int value){
if(head==NULL){
insertAtHead(head,value);
}
Node* newNode = new Node();
newNode->data = value;
newNode->next = NULL;
Node *temp = head;
while(temp->next!=NULL){
temp = temp->next;
}
temp->next = newNode;
cout<<"Added "<<newNode->data<<" at the end"<<endl;
}
void searchAndDelete(Node **headPtr, int searchItem){
Node *temp = new Node();
if( (*headPtr)->data == searchItem ){
temp = *headPtr;
*headPtr = (*headPtr)->next;
free(temp);
}else{
Node *currentNode = *headPtr;
while(currentNode->next != NULL){
if(currentNode->next->data == searchItem){
temp = currentNode->next;
currentNode->next = currentNode->next->next;
free(temp);
}else{
currentNode = currentNode->next;
}
}
}
cout<<"Deleted Node\t"<<searchItem<<endl;
return;
}
void insertAfter(Node * &headPtr, int searchItem, int value){
Node* newNode = new Node();
newNode->data = value;
newNode->next = NULL;
Node *head = headPtr;
while(head->next!=NULL && head->data!=searchItem){
head = head->next;
}
newNode->next = head->next;
head->next = newNode;
cout<<"Inserted "<<value<<" after node\t"<<searchItem<<endl;
}
void insertBefore(Node * &headPtr, int searchItem, int value){
Node* newNode = new Node();
newNode->data = value;
newNode->next = NULL;
Node *head = headPtr;
while(head->next!=NULL && head->next->data!=searchItem){
head = head->next;
}
newNode->next = head->next;
head->next = newNode;
cout<<"Inserted "<<value<<" before node\t"<<searchItem<<endl;
}
void traverse(Node *headPointer){
Node* tempNode = new Node();
tempNode = headPointer;
cout<<"Traversal from head:\t";
while(tempNode !=NULL){
cout<<tempNode->data;
if(tempNode->next)
cout<<" --> ";
tempNode = tempNode ->next;
}
cout<<endl;
}
int main(){
Node *head = NULL;
insertAtHead(head,5);
insertAtHead(head,6);
insertAtHead(head,7);
insertEnd(head,9);
traverse(head);
searchAndDelete(&head,6);
traverse(head);
insertAfter(head,7,10);
insertBefore(head,9,11);
traverse(head);
}
输出
Added 5 at the front Added 6 at the front Added 7 at the front Added 9 at the end Traversal from head: 7 → 6 → 5 → 9 Deleted Node 6 Traversal from head: 7 → 5 → 9 Inserted 10 after node 7 Inserted 11 before node 9 Traversal from head: 7 → 10 → 5 → 11 → 9
Python 程序中的单向链表示例
class Node:
def __init__(self,data = None, next = None):
self.data = data
self.next = next
class SinglyLinkedList:
def __init__(self):
self.head = None
def insertAtHead(self, value):
newNode = Node(data=value)
if self.head is not None:
newNode.next = self.head
self.head = newNode
print(f'Added {newNode.data} at the front.')
return
def insertAtEnd(self,value):
if self.head is None:
self.insertAtHead(value)
newNode = Node(value)
temp = self.head
while temp.next is not None:
temp = temp.next
temp.next = newNode
print(f'Added {newNode.data} at the end.')
def searchAndDelete(self,searchItem):
temp = Node()
if self.head is searchItem:
temp = self.head
self.head = self.head.next
else:
currentNode = self.head
while currentNode.next is not None:
if currentNode.next.data is searchItem:
temp = currentNode.next
currentNode.next = currentNode.next.next
else:
currentNode = currentNode.next
print(f'Deleted node\t{searchItem}')
return
def insertAfter(self,searchItem,value):
newNode = Node(data=value)
temp = self.head
while temp.next is not None and temp.data is not searchItem:
temp = temp.next
newNode.next = temp.next
temp.next = newNode
print(f'Inserted {value} after node\t{searchItem}')
return
def insertbefore(self,searchItem,value):
newNode = Node(data=value)
temp = self.head
while temp.next is not None and temp.next.data is not searchItem:
temp = temp.next
newNode.next = temp.next
temp.next = newNode
print(f'Inserted {value} before node\t{searchItem}')
return
def traverse(self):
temp = self.head
print("Traversing from head:\t",end="")
while temp:
print("{}\t".format(temp.data),end="")
temp = temp.next
print()
SinglyLinkedList = SinglyLinkedList()
SinglyLinkedList.insertAtHead(5)
SinglyLinkedList.insertAtHead(6)
SinglyLinkedList.insertAtHead(7)
SinglyLinkedList.insertAtEnd(9)
SinglyLinkedList.traverse()
SinglyLinkedList.searchAndDelete(6)
SinglyLinkedList.traverse()
SinglyLinkedList.insertAfter(7,10)
SinglyLinkedList.insertbefore(9, 11)
SinglyLinkedList.traverse()
输出
Added 5 at the front. Added 6 at the front. Added 7 at the front. Added 9 at the end. Traversing from head: 7 6 5 9 Deleted node 6 Traversing from head: 7 5 9 Inserted 10 after node 7 Inserted 11 before node 9 Traversing from head: 7 10 5 11 9
单向链表的复杂度
有两种复杂度:时间复杂度和空间复杂度。单向链表的最好、平均和最坏情况时间复杂度是相同的。
最好情况下的时间复杂度:
- 头部插入可以在 O(1) 内完成。因为我们不需要遍历链表内部。
- 如果搜索元素存在于头节点,则搜索和删除操作可以在 O(1) 内完成。
平均情况下的时间复杂度
- 如果单向链表中存在“n”个元素,则在链表内插入需要 O(n)。
- 搜索和删除也可以是 O(n),因为搜索元素可能存在于尾节点。在这种情况下,您应该遍历整个列表。
单向链表的空间复杂度
单向链表动态分配内存。如果要存储 n 个元素,它将分配 n 个内存单元。因此,空间复杂度为 O(n)。
