质因数分解算法:C、Python 示例
什么是质因数分解?
一个给定**任何**数字的质因数是指该因数是一个**质数**。当相乘得到另一个数字的因数。质数只能被它本身或 1 整除。
换句话说,质因数是通过找出哪些质数相乘得到原始数字来确定的。
示例:10 的质因数是 2 和 5。因为 2X5 = 10,而 2 和 5 都是质数。
使用迭代查找质因数
要找到给定数字的质因数,我们首先从 2 迭代到该数字的平方根,然后检查每个数字是否是质数。只要原始数字能被这个质数整除,我们就每次迭代都将这个质数添加进去。
示例
大于 40 的每个质数都写成以下公式:n2+n+41。因此,我们可以用所有数字替换 n 来找到相应的质因数。例如:02+0+41=41,12+1+41=43,22+2+41=47,……
如何打印一个数字的质因数?
- 在此方法中,我们将从 2 迭代到数字的平方根,如前一节所述。
- 为此,我们需要检查原始数字对 2 到 n 的平方根之间的每个数字的模。
- 然后,我们找出作为 n 的因数的质数列表。
- 此解决方案的时间复杂度为 O(Sqrt(n))。
算法
Set a counter i to 2 While i <= sqrt(n): While n% i == 0: n = n / i print i i = i +1 if n > 1: print n
埃拉托斯特尼筛法
筛法依赖于存储数字的最小质因数,这在计算任何数字的质因数时能显著降低复杂度。筛法算法能相对有效地找到所有质因数。
- 此算法的主要概念是存储每个数字直到最大数字的最小质因数。
- 我们取每个给定数字的最小质数,并将其添加到质因数集中。
- 最后,我们除以这个质数,并重复这些步骤直到达到 1。
- 这一切都以 O(log(n)) 的时间复杂度完成,大大提高了解决方案的效率。
- 这使得我们能够计算比使用前一种方法能处理的数字大得多的数字的质因数。
示例
第二种方法是检查该数字是否可以写成 6n-1 或 6n+1 的形式,因为除了 2 和 3 之外的任何质数都应该写成这两种形式之一。例如:5=6(1)-1,19=6(3)+1,…… 。
算法
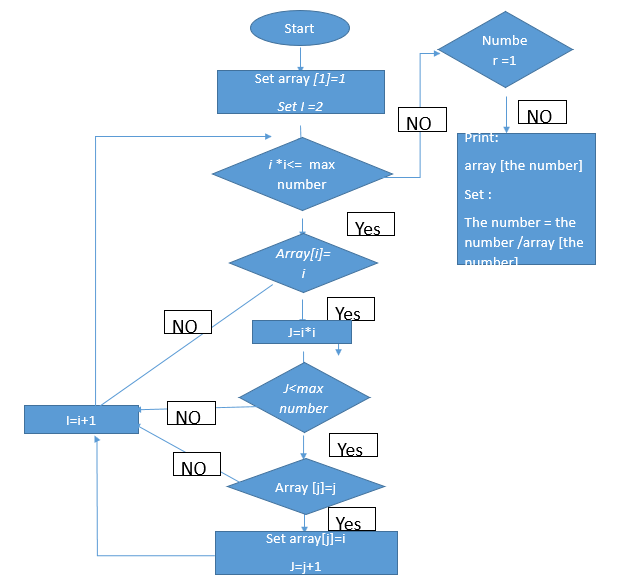
定义一个数组 array 来存储每个数字的最小质因数,其中索引值是每个数组元素的初始值。
Set array[1] to 1 Set i to 2 While i*i > max number: If array[i] == i: Set j to i*i While j > max number: If array[j] == j: Array[j] = i j = j + i i = i + 1 while the number != 1: print array[the number] the number = the number / array[the number]
Python 迭代查找质因数
在这里,我们将展示一个 Python 语言的代码,用于以迭代方式查找给定数字的质因数。
import math
def PrimeFactors(n):
for i in range(2,int(math.sqrt(n))+1,1):
while n%i==0:#find all the occurrences of a prime factor
print((int)(i)),
n=n/i
if n!=1:#if the number was originally a prime
print((int)(n))
n=(int)(input("Enter the number you want: "))
PrimeFactors(n)
输出
Enter the number you want: 4 4
Python 递归查找质因数
本节将使用筛法在 Python 语言中展示一个代码,用于查找给定数字的质因数。
import math
High = (int)(1e5+7)
array=[0 for i in range(High)]
# function to generate all the smallest prime
def Sieve():
#factors of the numbers until the maximum number
for i in range(1, High):
array[i]=i
for i in range(2, math.ceil(math.sqrt(High))):
if (array[i] == i):
for j in range(i*i, High,i):
if(array[j]==j):
array[j]=i
def PrimeFactors(n):
#We will keep dividing until we reach 1
if n == 1:
return
print((int)(array[n]))
PrimeFactors((int)(n/array[n]))
#Here we call the function after dividing it by this prime
Sieve()
n=(int)(input("Enter the number you want: "))
PrimeFactors(n)
输出
Enter the number you want: 4 2 2
C 语言迭代质因数程序
这是与迭代 Python 版本相同的解决方案,但用 C 语言编写。
我们要求用户输入数字,然后对于从 2 到该数字平方根的每个数字,我们需要检查它是否可被整除,并打印出该因数的所有出现次数。
#include <stdio.h>
int main()
{
int n;
printf("Enter the number you want: ");
scanf("%d", &n);
for(int i=2; i*i<=n; i++)
{
while(n%i==0)//find all the occurrences of a prime factor
{
printf("%d\n",i);
n/=i;
}
}
if(n!=1)//if the number was originally a prime
{
printf("%d",n);
}
return 0;
}
输出
Enter the number you want: 2 2
C 语言递归质因数程序
这是与 Python 递归版本相同的解决方案,但用 C 语言编写。
我们可以要求用户输入数字;然后,我们构建 primes 数组,该数组存储每个数字的最小质因数。最后,我们调用 Prime Factors 递归函数,该函数将给定数字除以其最小质因数,并一直递归调用直到达到一。
#include <stdio.h>
int Max = 100007;
int array[100007];
void Sieve()//helping function to generate all the smallest //prime factors of the numbers until the maximum number
{
for(int i=1;i<Max;i++)
{
array[i]=i;
}
for(int i=2;i*i<=Max;i++)
{
if(array[i]==i)
{
for(int j=i*i;j<Max;j+=i)
{
if(array[j]==j)
{
array[j]=i;
}
}
}
}
}
void PrimeFactors(int n)
{
if(n==1)//keep dividing until we reach 1
{
return;
}
printf("%d\n",array[n]);
PrimeFactors(n/array[n]);//call the function after dividing by //this prime
}
int main()
{
Sieve();
int n;
printf("Enter the number you want: ");
scanf("%d", &n);
PrimeFactors(n);
return 0;
}
输出
Enter the number you want: 2 2
关于质数的一些有趣事实
- 最有趣的事实之一是,除了 2 之外的任何偶数都可以是两个质数的和。
- 例如:4 = 2 + 2,6 = 3 + 3,8 = 5 + 3 …… 等。
- 另一个事实是,除了 2 和 3 之外,没有连续的质数,因为唯一的偶质数是数字 2。
- 同样,除了 2 和 3 之外,所有质数都可以写成以下形式:6 * n + 1 或 6 * n – 1,其中 n 是正整数。
- 一个数字的质因数集是唯一的。
- 数字 1 既不是质数也不是合数。
- 数字的质因数分解可以帮助解决可除性、简化分数和查找不同分数的公分母等问题。
- 此外,质因数分解的一个令人兴奋的用途是破解基于数字的秘密密码。