桶排序算法(Java、Python、C/C++ 代码示例)
什么是桶排序?
桶排序,也称为箱排序,是一种比较排序方法,它接受一个未排序的数组作为输入,并产生一个已排序的数组作为输出。该方法通过将元素分配到几个桶中,然后使用插入排序等任何排序算法对每个桶进行单独排序。之后,将所有桶合并以形成一个排序后的数组。
桶排序通常用于以下情况的元素:
- 浮点数值
- 在某个范围内均匀分布
桶排序的时间复杂度取决于使用的桶的数量和输入分布的均匀性。虽然诸如希尔排序、归并排序、堆排序和快速排序等不同的排序算法可以达到 O(n*logn) 的最佳时间复杂度,但桶排序算法可以在线性时间复杂度 O(n) 中实现相同的目标。
桶排序遵循散布-收集(scatter-gather)方法。采用这种方法,元素被散布到相应的桶中,在桶中进行排序,然后收集起来作为最后一步形成排序后的数组。这种散布-收集方法将在下一节中讨论。
散布-收集方法
规模大、复杂的问题有时难以解决。散布-收集方法通过将整个数据集划分为簇来尝试解决这类问题。然后单独处理每个簇,并将所有内容重新组合以得到最终答案。
这就是桶排序算法实现散布-收集方法的方式。
桶排序的工作原理
桶排序的基本工作原理如下:
- 创建一组空桶。根据不同的策略,桶的数量可能会有所不同。
- 从输入数组中,将每个元素放入其相应的桶中。
- 对这些桶进行单独排序。
- 连接排序后的桶以创建单个输出数组。
详细的工作步骤将在以下各节中提供。
伪代码
Start Create N empty buckets For each array element: Calculate bucket index Put that element into the corresponding bucket For each bucket: Sort elements within each bucket Merge all the elements from each bucket Output the sorted array End
方法 1:用于浮点数的桶排序算法
范围在 0.0 到 1.0 之间的浮点数的桶排序算法
步骤 1) 创建十(10)个空桶,第一个桶将包含范围 [0.0, 0.1) 内的数字。然后第二个桶将包含范围 [0.1, 0.2) 内的数字,依此类推。
步骤 2) 对于每个数组元素
- a. 使用以下公式计算桶索引
桶索引 = 桶数 * 数组元素
- b. 将元素插入 bucket[bucket_index]
步骤 3) 使用插入排序对每个桶进行单独排序。
步骤 4) 连接所有桶以形成一个数组。
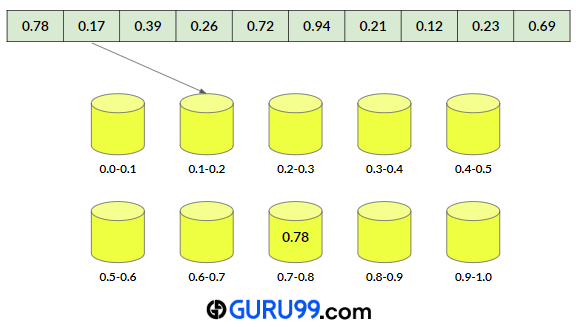
让我们看一个桶排序的例子。在此示例中,我们将使用桶排序算法对以下数组进行排序:
步骤 1) 首先,我们将创建 10 个空桶。第一个桶将包含 0.0 到 0.1 之间的数字。然后第二个桶将包含 0.1 到 0.2 之间的数字,依此类推。
步骤 2) 对于每个数组元素,我们将计算桶索引并将元素放入该桶中。
桶索引可以使用以下公式计算:
桶索引= 桶数*数组元素
桶索引计算
a) 0.78
桶索引 = 桶数*数组元素
=10*0.78
= 7.8
因此,元素 0.78 将存储在 bucket[floor(7.8)] 或 bucket[7] 中。
b) 0.17
桶索引 = 桶数 * 数组元素
=10*0.17
= 1.7
数组元素 0.17 将存储在 bucket[floor(1.7)] 或 bucket[1] 中。
c) 0.39
桶索引 = 桶数 * 数组元素
= 10*0.39
= 3.9
0.39 将存储在 bucket[floor(3.9)] 或 bucket[3] 中。
遍历所有数组元素后,桶将如下所示:
步骤 3) 然后,将使用插入排序对每个桶进行排序。排序后,输出将是:
步骤 4) 在最后一步,将所有桶连接成一个数组。该数组将是输入数组的排序结果。
每个桶都将连接到输出数组。例如,第二个桶元素的连接。
最后一个桶元素的连接将是:
连接后,结果数组将是我们想要的排序数组。
C/C++ 中的桶排序程序
输入
//Bucket Sort Program in C/C++
//For not having integer parts
#include <bits/stdc++.h>
#define BUCKET_SIZE 10
using namespace std;
void bucketSort(float input[], int array_size)
{
vector <float>bucket[BUCKET_SIZE];
for (int i = 0; i < array_size; i++) {
int index = BUCKET_SIZE*input[i];
bucket[index].push_back(input[i]);
}
for (int i = 0; i < BUCKET_SIZE; i++)
sort(bucket[i].begin(), bucket[i].end());
int out_index = 0;
for (int i = 0; i < BUCKET_SIZE; i++)
for (int j = 0; j < bucket[i].size(); j++)
input[out_index++] = bucket[i][j];
}
int main()
{
float input[]={0.78,0.17,0.39,0.26,0.72,0.94,0.21,0.12,0.23,0.69};
int array_size = sizeof(input)/sizeof(input[0]);
bucketSort(input, array_size);
cout <<"Sorted Output: \n";
for (int i = 0; i< array_size; i++)
cout<<input[i]<<" ";
return 0;
}
输出
Sorted Output: 0.12 0.17 0.21 0.23 0.26 0.39 0.69 0.72 0.78 0.94
Python 中的桶排序程序
输入
# Bucket Sort Program in Python
# For not having integer parts
def bucketSort(input):
output = []
bucket_size = 10
for bucket in range(bucket_size):
output.append([])
for element in input:
index = int(bucket_size * element)
output[index].append(element)
for bucket in range(bucket_size):
output[bucket] = sorted(output[bucket])
out_index = 0
for bucket in range(bucket_size):
for element in range(len(output[bucket])):
input[out_index] = output[bucket][element]
out_index += 1
return input
input = [0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.12, 0.23, 0.69]
print("Sorted Output:")
print(bucketSort(input))
输出
Sorted Output: [0.12, 0.17, 0.21, 0.23, 0.26, 0.39, 0.69, 0.72, 0.78, 0.94]
Java 中的桶排序
输入
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class BucketSort {
private static final int BUCKET_SIZE = 10;
public static void bucketSort(float[] input, int arraySize) {
List <
Float >
[] bucket = new ArrayList[BUCKET_SIZE];
for (int i = 0; i < arraySize; i++) {
int index = (int)(BUCKET_SIZE * input[i]);
if (bucket[index] == null) {
bucket[index] = new ArrayList < >
();
}
bucket[index].add(input[i]);
}
for (int i = 0; i < BUCKET_SIZE; i++) {
if (bucket[i] != null) {
Collections.sort(bucket[i]);
}
}
int outIndex = 0;
for (int i = 0; i < BUCKET_SIZE; i++) {
if (bucket[i] != null) {
for (float value: bucket[i]) {
input[outIndex++] = value;
}
}
}
}
public static void main(String[] args) {
float[] input = {0.78f,0.17f,0.39f,0.26f,0.72f,0.94f,0.21f,0.12f,0.23f,0.69f};
int arraySize = input.length;
bucketSort(input, arraySize);
System.out.println("Sorted Output:");
for (int i = 0; i < arraySize; i++) {
System.out.print(input[i]+" ");
}
}
}
输出
Sorted Output: 0.12 0.17 0.21 0.23 0.26 0.39 0.69 0.72 0.78 0.94
方法 2:用于整数元素的桶排序算法
对于包含超出 [0.0, 1.0] 范围的数字的输入的桶排序算法与之前的算法略有不同。此情况所需的步骤如下:
步骤 1) 找到最大和最小元素。
步骤 2) 选择桶的数量 n,并将这些桶初始化为空。
步骤 3) 使用以下公式计算每个桶的范围或跨度:
跨度 = (最大值 - 最小值) / n
步骤 4) 对于每个数组元素
- 1.计算桶索引
桶索引 = (元素 - 最小值) / 跨度- 2.将元素插入 bucket[bucket_index]
步骤 5) 使用插入排序对每个桶进行排序。
步骤 6) 将所有桶连接成一个数组。
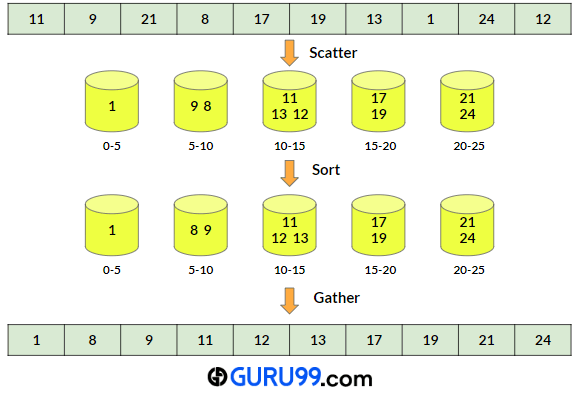
让我们看一个这个桶排序算法的例子。在此示例中,我们将使用桶排序算法对以下数组进行排序:
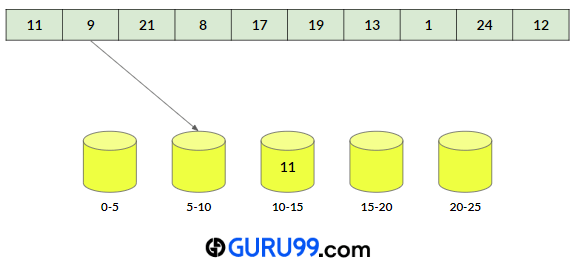
步骤 1) 第一步,需要找出给定数组的最大和最小元素。在此示例中,最大值为 24,最小值为 1。
步骤 2) 现在,我们需要选择一个空桶的数量 n。在本例中,我们将使用 5 个桶。然后将它们初始化为空。
步骤 3) 每个桶的跨度需要通过以下公式计算:
跨度 = (最大值-最小值)/n = (24-1)/5 = 4;
因此,第一个桶将包含范围 [0, 5) 内的数字。第二个桶将包含范围 [5, 10) 内的数字,依此类推。
步骤 4) 对于每个数组元素,我们将计算桶索引并将元素放入该桶中。桶索引可以使用以下公式计算:
桶索引 = (元素 - 最小值) / 跨度
桶索引计算
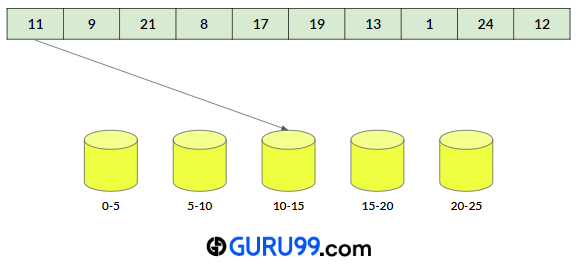
- a) 11桶索引 = (元素 – 最小值)/跨度
=(11-1)/4
=2
因此,元素 11 将存储在 bucket[2] 中。
- b) 9
桶索引 = (元素 – 最小值)/跨度
=(9-1)/4
=2
注意:由于 9 是 bucket[1] 的边界元素,因此需要将其附加到 bucket[1] 中,而不是附加到前一个元素的相同桶中。
在为每个元素执行操作后,桶将如下所示:
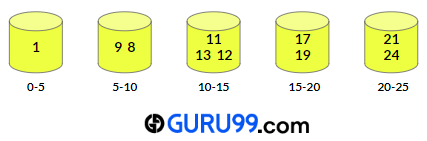
步骤 5) 现在,将使用插入排序对每个桶进行排序。排序后的桶:
步骤 6) 在最后一步,将所有桶连接成一个数组。该数组将是输入数组的排序结果。
C/C++ 中的桶排序程序
输入
#include<bits/stdc++.h>
using namespace std;
void bucketSort(vector < double > & input, int No_Of_Buckets)
{
double max_value = * max_element(input.begin(), input.end());
double min_value = * min_element(input.begin(), input.end());
double span = (max_value - min_value) / No_Of_Buckets;
vector<vector <double>>
output;
for (int i = 0; i < No_Of_Buckets; i++)
output.push_back(vector <double>
());
for (int i = 0; i < input.size(); i++)
{
double difference = (input[i] - min_value) / span
-
int((input[i] - min_value) / span);
if (difference == 0 && input[i] != min_value)
output[int((input[i] - min_value) / span) - 1]
.push_back(input[i]);
else
output[int((input[i] - min_value) / span)].push_back(
input[i]);
}
for (int i = 0; i < output.size(); i++)
{
if (!output[i].empty())
sort(output[i].begin(), output[i].end());
}
int index = 0;
for (vector <double> & bucket: output)
{
if (!bucket.empty())
{
for (double i: bucket)
{
input[index] = i;
index++;
}
}
}
}
int main()
{
vector <double>
input ={11,9,21,8,17,19,13,1,24,12
};
int No_Of_Buckets = 5;
bucketSort(input, No_Of_Buckets);
cout<<
"Sorted Output:";
for (int i; i < input.size(); i++)
cout <<input[i]<<" ";
return 0;
}
输出
Sorted Output:1 8 9 11 12 13 17 19 21 24
Python 中的桶排序程序
输入
def bucketSort(input, No_Of_Buckets):
max_element = max(input)
min_element = min(input)
span = (max_element - min_element) / No_Of_Buckets
output = []
for bucket in range(No_Of_Buckets):
output.append([])
for element in range(len(input)):
diff = (input[element] - min_element) / span - int(
(input[element] - min_element) / span
)
if diff == 0 and input[element] != min_element:
output[int((input[element] - min_element) / span) - 1].append(
input[element]
)
else:
output[int((input[element] - min_element) / span)].append(input[element])
for bucket in range(len(output)):
if len(output[bucket]) != 0:
output[bucket].sort()
index = 0
for bucket in output:
if bucket:
for element in bucket:
input[index] = element
index = index + 1
input = [11, 9, 21, 8, 17, 19, 13, 1, 24, 12]
No_Of_Buckets = 5
bucketSort(input, No_Of_Buckets)
print("Sorted Output:\n", input)
输出
Sorted Output: [1, 8, 9, 11, 12, 13, 17, 19, 21, 24]
Java 中的桶排序
输入
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class BucketSort {
public static void bucketSort(List < Double > input, int No_Of_Buckets) {
double max_value = Collections.max(input);
double min_value = Collections.min(input);
double span =(max_value - min_value) / No_Of_Buckets;
List <
List <
Double > >
output = new ArrayList < >
();
for (int i = 0; i < No_Of_Buckets; i++) {
output.add(new ArrayList < >
());
}
for (Double value: input) {
double difference = (value - min_value) / span - ((value - min_value) / span);
if (difference == 0 && value != min_value) {
output.get((int)((value - min_value) / span) - 1).add(value);
} else {
output.get((int)((value - min_value) / span)).add(value);
}
}
for (List <Double> bucket: output) {
if (!bucket.isEmpty()) {
Collections.sort(bucket);
}
}
int index = 0;
for (List <Double> bucket: output) {
if (!bucket.isEmpty()) {
for (Double value: bucket) {
input.set(index,value);
index++;
}
}
}
}
public static void main(String[] args) {
List <Double>
input = new ArrayList <>
();
input.add(11.0);
input.add(9.0);
input.add(21.0);
input.add(8.0);
input.add(17.0);
input.add(19.0);
input.add(13.0);
input.add(1.0);
input.add(24.0);
input.add(12.0);
int No_Of_Buckets = 5;
bucketSort(input, No_Of_Buckets);
System.out.println("Sorted Output:");
for (Double value: input) {
System.out.print(value + " ");
}
}
}
输出
Sorted Output: 1.0 8.0 9.0 11.0 12.0 13.0 17.0 19.0 21.0 24.0
优点与缺点
| 优点 | 缺点 |
|---|---|
| 执行更快的计算 | 比其他算法消耗更多空间 |
| 可用作外部排序方法 | 当数据分布不均匀时,性能不佳 |
| 桶可以独立处理 |
桶排序复杂度分析
桶排序的时间复杂度
- 最佳情况复杂度:如果所有数组元素都均匀分布并且事先已排序,则将元素散布到相应桶中需要 O(n) 时间。然后使用插入排序对每个桶进行排序将花费 O(k) 时间。因此,总复杂度为 O(n+k)。
- 平均情况复杂度:对于平均情况,我们假设输入是均匀分布的。因此,桶排序算法可以达到线性时间复杂度 O(n+k)。这里 O(n) 时间用于散布元素,O(k) 时间用于使用插入排序对这些元素进行排序。
- 最坏情况复杂度:在最坏的情况下,元素不会均匀分布,而是集中在一个或两个特定桶中。在这种情况下,桶排序将作为冒泡排序算法运行。因此,在最坏的情况下,桶排序的时间复杂度将为 O(n^2)。
桶排序的空间复杂度
桶排序的空间复杂度为 O(n*k)。其中 n 是元素数量,k 是所需的桶数量。