Shell Sort 算法及示例
什么是希尔排序
希尔方法,或称数据结构中的希尔排序,是一种高效的原地比较排序算法。它以 Donald Shell 在 1959 年提出初步想法命名。希尔排序是插入排序算法的泛化扩展。
这种排序算法的基本思想是对相距较远的元素进行分组并相应地排序。然后逐渐减小它们之间的间隙。希尔排序通过比较和交换相距较远的元素来克服插入排序的平均情况时间复杂度。
这个间隙,称为间隔,根据一些最优的间隙序列进行减小。希尔排序的运行时间也取决于这些序列。有几种间隙序列,如 Shell 的原始序列、Knuth 公式、Hibbard 的增量等。Shell 的原始间隙序列是 - n/2, n/4, n/8, ……….1
希尔排序算法
希尔排序算法的步骤或过程如下:
步骤 1) 初始化间隔值,h = n/2。(在此示例中,n 是数组的大小)
步骤 2) 将间隔为 h 的所有元素放入一个子列表。
步骤 3) 使用插入排序对这些子列表进行排序。
步骤 4) 设置新间隔,h=h/2。
步骤 5) 如果 h>0,则转到步骤 2。否则转到步骤 6。
步骤 6) 结果输出将是已排序的数组。
希尔排序如何工作
在插入排序中,元素一次只移动一个位置。相反,希尔排序根据间隔值将数组分成更小的部分,并对这些部分执行插入排序。
逐渐地,间隔值减小,划分的部分大小增加。由于各个部分事先已排序,合并这些部分所需的步骤比插入排序少。
下面的 GIF 展示了希尔排序的演示。在此演示中,红色和蓝色的值根据插入排序进行比较和交换。然后间隔减小,希尔排序对该几乎排序的数据启动插入排序。
希尔排序算法的工作原理
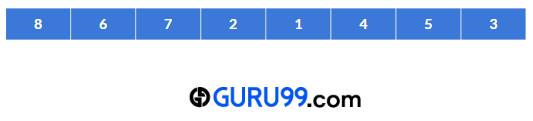
让我们来看一个希尔排序算法的示例。在此示例中,我们将使用希尔排序对以下数组进行排序:
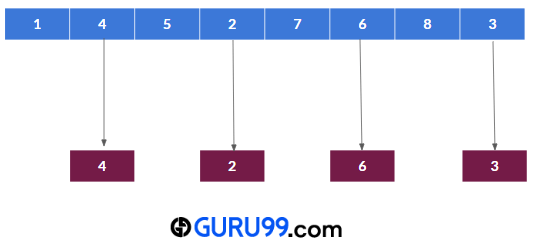
步骤 1) 这里,数组大小为 8。因此,间隔值将是 h = 8/2 或 4。
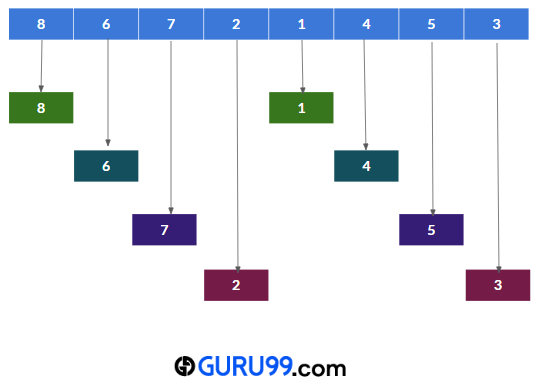
步骤 2) 现在,我们将存储所有相距 4 的元素。在本例中,子列表为 - {8, 1}, {6, 4}, {7, 5}, {2, 3}。
步骤 3) 现在,将使用插入排序对这些子列表进行排序,其中使用临时变量来比较两个数字并相应地排序。
交换操作后,数组将如下所示:
步骤 4) 现在,我们将减小间隔的初始值。新间隔将是 h=h/2 或 4/2 或 2。
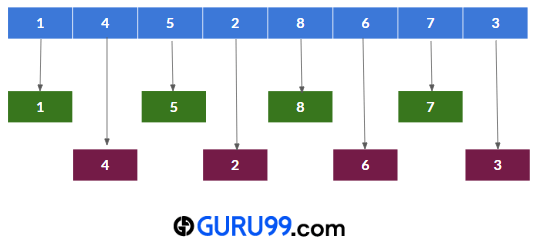
步骤 5) 由于 2>0,我们将转到步骤 2,将所有相距 2 的元素存储起来。这次,子列表是 -
{1, 5, 8, 7}, {4, 2, 6, 3}
然后将使用插入排序对这些子列表进行排序。比较和交换第一个子列表后,数组将如下所示:
对第二个子列表排序后,原始数组将是
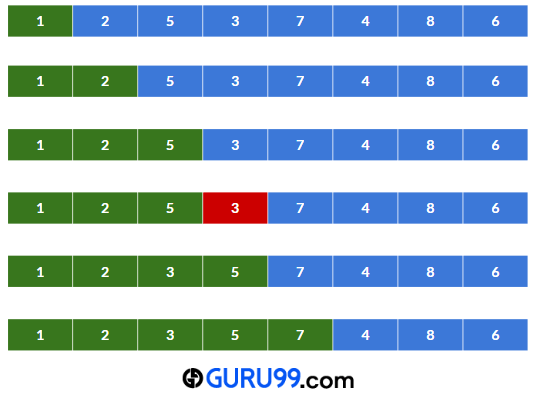
然后再次减小间隔。现在间隔将是 h=h/2 或 2/1 或 1。因此,我们将使用插入排序算法对修改后的数组进行排序。
以下是插入排序的分步程序图。
间隔再次除以 2。此时,间隔变为 0。所以我们转到步骤 6。
步骤 6) 由于间隔为 0,此时数组已排序。排序后的数组是 -
伪代码
Start
Input array an of size n
for (interval = n / 2; interval & gt; 0; interval /= 2)
for (i = interval; i & lt; n; i += 1)
temp = a[i];
for (j = i; j & gt; = interval & amp; & amp; a[j - interval] & gt; temp; j -= interval)
a[j] = a[j - interval];
a[j] = temp;
End
希尔排序 C/C++ 程序
输入
//Shell Sort Program in C/C++
#include <bits/stdc++.h>
using namespace std;
void ShellSort(int data[], int size) {
for (int interval = size / 2; interval > 0; interval /= 2) {
for (int i = interval; i < size; i += 1) {
int temp = data[i];
int j;
for (j = i; j >= interval && data[j - interval] > temp; j -= interval) {
data[j] = data[j - interval];
}
data[j] = temp;
}
}
}
int main() {
int data[] = {8, 6, 7, 2, 1, 4, 5, 3};
int size = sizeof(data) / sizeof(data[0]);
ShellSort(data, size);
cout << "Sorted Output: \n";
for (int i = 0; i < size; i++)
cout << data[i] << " ";
cout << "\n";
}
输出
Sorted Output: 1 2 3 4 5 6 7 8
Python 中的希尔排序示例
输入
#Shell Sort Example in Python
def ShellSort(data, size):
interval = size // 2
while interval > 0:
for i in range(interval, size):
temp = data[i]
j = i
while j >= interval and data[j - interval] > temp:
data[j] = data[j - interval]
j -= interval
data[j] = temp
interval //= 2
data = [8, 6, 7, 2, 1, 4, 5, 3]
ShellSort(data, len(data))
print('Sorted Output:')
print(data)
输出
Sorted Output: [1, 2, 3, 4, 5, 6, 7, 8]
希尔排序的应用
以下是希尔排序的重要应用
- 希尔排序用于Linux 内核,因为它不使用调用堆栈。
- uClibc 库使用希尔排序。
- bzip2 压缩器使用希尔排序来防止递归过载。
希尔排序的优缺点
| 优点 | 缺点 |
|---|---|
| 无需调用堆栈。 | 对于巨大的数组大小效率不高。 |
| 实现简单。 | 对于元素分布范围广的列表效率不高。 |
| 对于元素分布范围较窄的列表效率高。 |
希尔排序复杂度分析
希尔排序的时间复杂度
希尔排序算法的时间复杂度为 O(n^2)。其原因如下:
在最佳情况下,当数组先前排列好时,所有间隔的总测试次数约为 log n。因此,复杂度为 O(n*log n)。
在最坏情况下,我们考虑数组的排列方式,使得元素需要最多的比较次数。那么,直到最后一次迭代,所有元素都不会被比较和交换。因此,最后一次增量的总比较次数为 O(n^2)。
总之,时间复杂度将为
- 最佳情况复杂度:O(n*log n)
- 平均情况复杂度:O(n*log n)
- 最坏情况复杂度:O(n^2)
希尔排序的运行时间复杂度在很大程度上取决于所使用的间隔增量序列。然而,希尔排序的最佳增量序列仍然未知。
希尔排序空间复杂度
在此比较排序中,我们不需要任何额外的辅助空间。因此,这种排序算法的空间复杂度为 O(1)。