二分法 – 是什么、算法和示例

作者： Sarah Chen Sarah Chen
小时 - 权威教程 更新

什么是二分法？

二分法是用于查找多项式方程根的基本数值解之一。它将根所在的区间进行二分，并在每次迭代中将其细分为两半，直到找到根为止。因此，二分法也称为区间法。

然而，由于其工作机制与二分查找算法相似，二分法也称为二分查找法、折半法或分治法。它主要基于中间值定理。

求解方程的根

在此示例中，我们仅考虑具有一个自变量的方程。它可以是线性的也可以是非线性的。线性方程用于表示直线图，而非线性方程用于表示曲线。

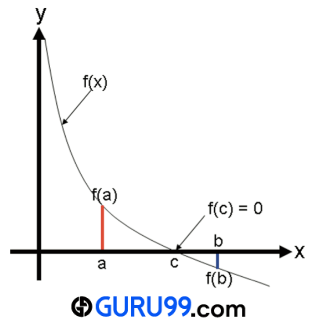
方程的根是指满足方程的自变量的值。例如：方程 f(x)= 4-x2 = 0 的根是 2，因为 f(2) = 4-22 =0。

令 f(x) 为一个连续实函数。根据中间值定理，如果 f(a)f(b) < 0，则方程 f(x)=0 在 a 和 b 之间至少有一个根。函数 f(x) 在 a 和 b 之间有一个根，“c”。

Finding Roots of Equations

二分法的图形表示

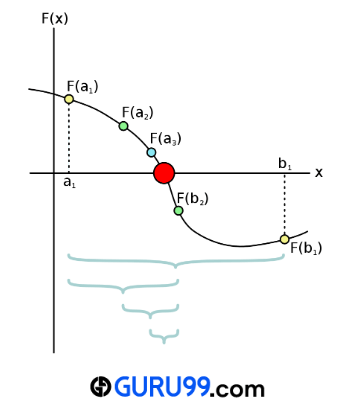
下图表示了二分法的工作机制。从图中可以看到，方程的根用红色标记。

开始

  • 我们首先取两个初始猜测值 a1 和 b1，使得 f(a1)f(b1) < 0。根据中间值定理，根应该落在 [a1, b1] 区间内。
  • 我们可以找到 a1 和 b1 的中点，即 b2。因此，由于 f(a1)f(b2) < 0，初始区间现在减小到 [a1, b2]。
  • 以同样的方式，区间被不断缩小，直到找到近似解。

Graphical Representation of Bisection Method

二分法算法

使用二分法算法查找方程 f(x)=0 的根的步骤如下：

步骤 1) 选择初始猜测值 a、b 和容差率 e

步骤 2) 如果 f(a)f(b) >=0，则根不在此区间内。因此，将没有解。

步骤 3) 计算中点，c = (a+b)/2

(i) 如果中点函数值 f(c) = 0，则 c 是根。转到步骤 5。
(ii) 如果 f(a)f(c) < 0，则根在 a 和 c 之间。则将 a = a，b = c。
(iii) 否则，将 a = c，b = b。

步骤 4) 如果绝对误差高于容差率或 (b-a) > e，则转到步骤 3。

步骤 5) 显示 c 作为近似根。

让我们看一个二分法算法的例子。
我们需要使用二分法公式找到以下连续函数的根。

f(x) = x3 – x2 + 2

二分法示例

步骤 1) 假设，

         a = -10，
         b = 10，以及
         e = 1% 或 0.01

步骤 2) 现在，我们将检查 f(a)f(b) 是否 >= 0。

         f(a) = f(-10) = (-10)3 – (-10)2 + 2 = -1098
         f(b) = f(10) = (10)3 – (10)2 + 2 = 902
         f(a)f(b) = f(-10)f(10) = (-1098)(902) < 0

因此，上述函数的根在此区间 [-10, 10] 内。

步骤 3) 然后将首先计算中点 c。

Bisection Method Example

现在需要检查以下条件：

(i) f(c) 是否 = 0
         f(c) = f(0) = (0)3 – (0)2 + 2 = 2 ≠ 0

(ii) 如果 f(a)f(c) < 0
         f(c)f(a) = 2*(-1098) < 0

该条件已满足。对于下一次迭代，值将是：

         a = a = -10
         b = c = 0

步骤 4) 由于 (b-a) = (0-(-10)) = 10 > 0.05，因此将重复该过程。下一次迭代显示在表格中。

迭代 a b c b-a f(c)
1 -10 0 0 10 2
2 -5 0 -5 5 -148
3 -2.5 0 -2.5 2.5 -19.875
4 -1.25 0 -1.25 1.25 -1.52562
5 -1.25 -0.625 -0.625 0.625 1.36523
6 -1.25 -0.9375 -0.9375 0.3125 0.297119
7 -1.09375 -0.9375 -1.09375 0.15625 -0.50473
8 -1.01562 -0.9375 -1.01562 0.078125 -0.0791054
9 -1.01562 -0.976562 -0.976562 0.0390625 0.115003
10 -1.01562 -0.996094 -0.996094 0.0195312 0.0194703
11 -1.00586 -0.996094 -1.00586 0.00976562 -0.0294344

步骤 5) 在第 11 次迭代中，步骤 4 的条件将为假。因此，该方程的根为 -1.00586。

相关文章

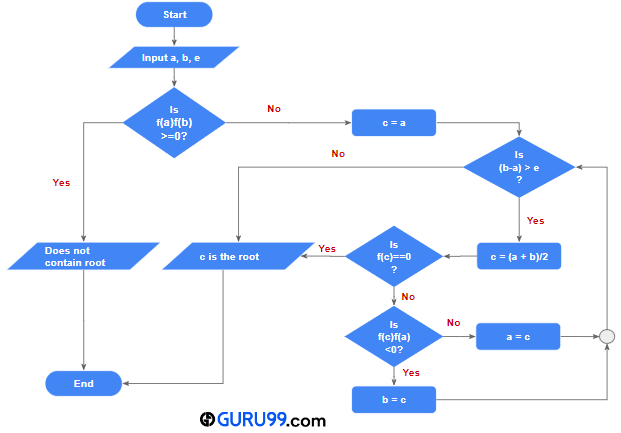
二分法逻辑图

Bisection Method Logical Diagram

伪代码

Start
Set a, b, e
if f(a)*f(b) >=0 
	Output("Root does not exist in this interval")
	Stop
while (b-a)>e do   
	c ← (a + b)/2    
	if f(c) = 0
        	break    
	end if 
	if f(c)*f(a) < 0 then
      	b ← c    
	else        
		a ← c
end while
Output(c)
Stop

C/C++ 中的二分法示例

输入

#include<bits/stdc++.h>
using namespace std;
#define Error 0.01
double value(double x)
{
	return x*x*x - x*x + 2;
}
void bisection_method(double a, double b)
{
	if (value(a) * value(b) >= 0)
	{
		cout << "The root does not lie in this interval\n";
		return;
	}
	double c = a;
	while ((b-a) >= Error)
	{
		c = (a+b)/2;
		if (value(c) == 0.0)
			break;
		else if (value(c)*value(a) < 0)
			b = c;
		else
			a = c;
	}
	cout << "The root is :" << c;
}
int main()
{
	double a =-10 , b = 10;
	bisection_method(a, b);
	return 0;
}

输出

The root is :-1.00586

Python 中的二分法示例

输入

def value(x):
	return x*x*x - x*x + 2
def bisection_method(a,b):
	if (value(a) * value(b) >= 0):
		return
	c = a
	while ((b-a) >= 0.01):
		c = (a+b)/2
		if (value(c) == 0.0):
			break
		if (value(c)*value(a) < 0):
			b = c
		else:
			a = c			
	print("The root is : ","%.4f"%c)	
a =-10
b = 10
bisection_method(a, b)

输出

The root is :  -1.0059

二分法的优点与局限性

以下是二分法的优点和缺点

优点 缺点
易于实现和简单的求根方法。 收敛速度慢，因为它只是基于对区间进行二分。
由于它对根进行区间限定，因此总是收敛的。 如果其中一个初始猜测值接近根，则达到根需要更多迭代。
可以通过增加或减少迭代次数来控制误差率。