AVL 树:C++ 示例的旋转、插入、删除
什么是AVL树?
AVL树是一种二叉搜索树,其中左子树和右子树的高度差为-1、0或+1。
AVL树也称为自平衡二叉搜索树。这些树有助于保持对数搜索时间。它以发明者(AVL)Adelson、Velsky和Landis的名字命名。
AVL树如何工作?
为了更好地理解AVL树的必要性,让我们看看普通二叉搜索树的一些缺点。
考虑以下键按给定顺序插入二叉搜索树。
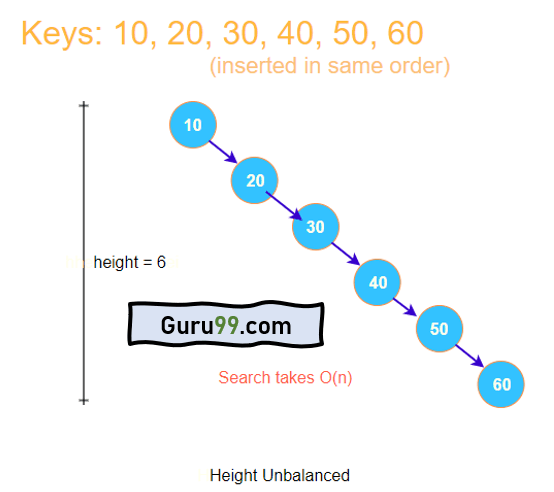
当以递增顺序插入键时,树的高度会线性增长。因此,最坏情况下搜索操作需要O(n)。
搜索元素需要线性时间;因此,使用二叉搜索树结构没有意义。另一方面,如果树的高度是平衡的,我们可以获得更好的搜索时间。
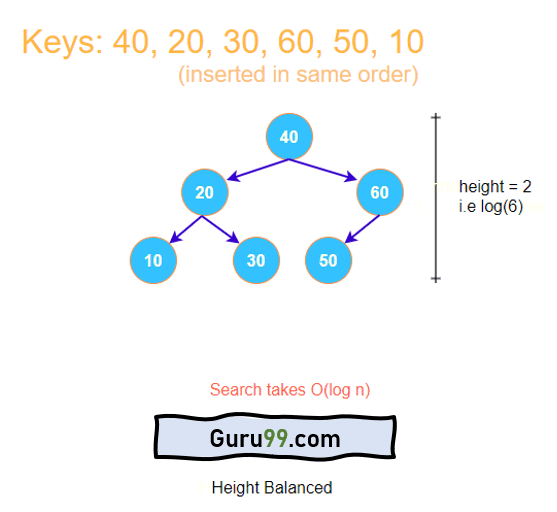
现在让我们看看相同的键,但以不同的顺序插入。
这里,键是相同的,但由于它们以不同的顺序插入,因此它们占据不同的位置,并且树的高度保持平衡。因此,对于树中的任何元素,搜索时间都不会超过O(log n)。现在很明显,如果插入得当,树的高度可以保持平衡。
在AVL树中,我们在插入操作期间检查树的高度。通过修改来保持平衡的高度,而不会违反二叉搜索树的基本属性。
AVL树中的平衡因子
平衡因子(BF)是AVL树中每个节点的根本属性,有助于监视树的高度。
平衡因子的性质
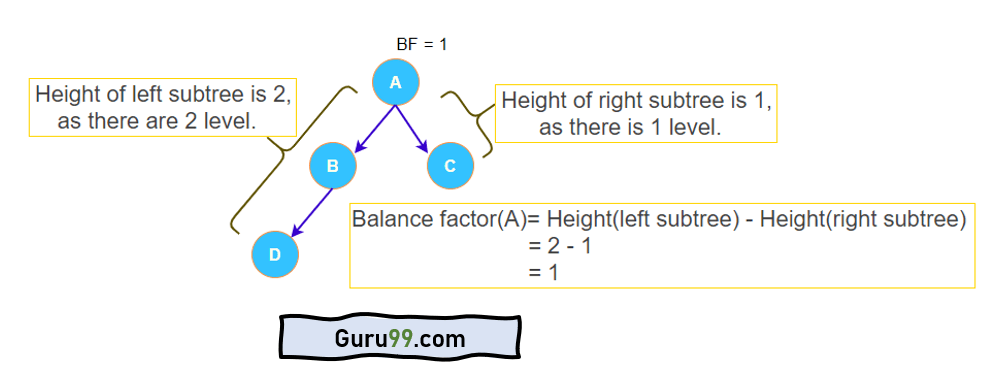
- 平衡因子是左子树高度与右子树高度之差。
- 平衡因子(节点) = 高度(节点->左) – 高度(节点->右)
- BF的允许值是–1、0和+1。
- 值–1表示右子树多一个节点,即树是右倾的。
- 值+1表示左子树多一个节点,即树是左倾的。
- 值0表示树两侧的节点数量相等,即树是完全平衡的。
AVL旋转
为了使AVL树在插入或删除树中的节点时保持平衡,会执行旋转操作。
我们执行以下LL旋转、RR旋转、LR旋转和RL旋转。
- 左-左旋转
- 右-右旋转
- 右-左旋转
- 左-右旋转
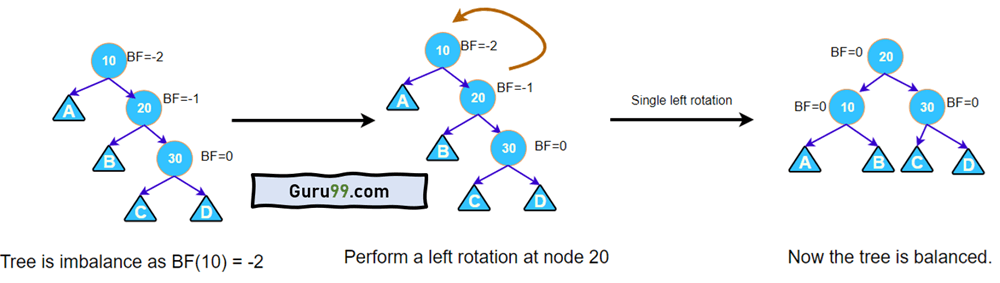
左-左旋转
当新节点插入到左子树的左孩子时,执行此旋转。
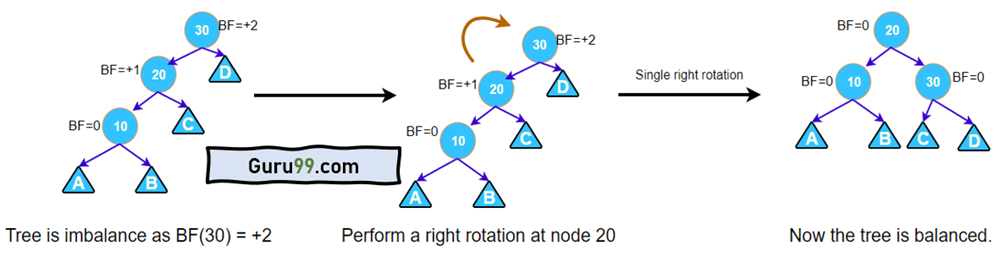
执行一次右旋转。当一个节点的平衡因子为+2,并且其左孩子的平衡因子为+1时,会识别出这种类型的旋转。
右-右旋转
当新节点插入到右子树的右孩子时,执行此旋转。
执行一次左旋转。当一个节点的平衡因子为-2,并且其右孩子的平衡因子为-1时,会识别出这种类型的旋转。
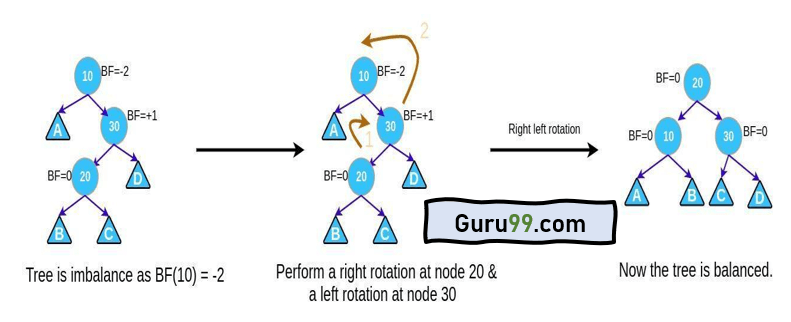
右-左旋转
当新节点插入到左子树的右孩子时,执行此旋转。
当一个节点的平衡因子为-2,并且其右孩子的平衡因子为+1时,执行此旋转。
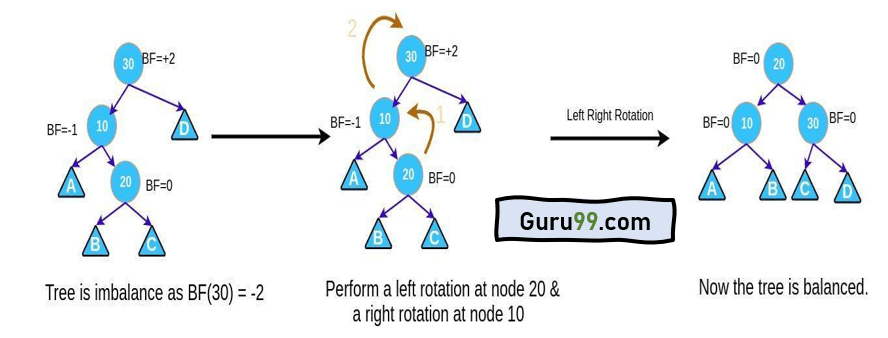
左-右旋转
当新节点插入到右子树的左孩子时,执行此旋转。
当一个节点的平衡因子为+2,并且其左孩子的平衡因子为-1时,执行此旋转。
AVL树中的插入
插入操作几乎与普通二叉搜索树中的操作相同。每次插入后,我们会平衡树的高度。插入操作的最坏时间复杂度为O(log n)。
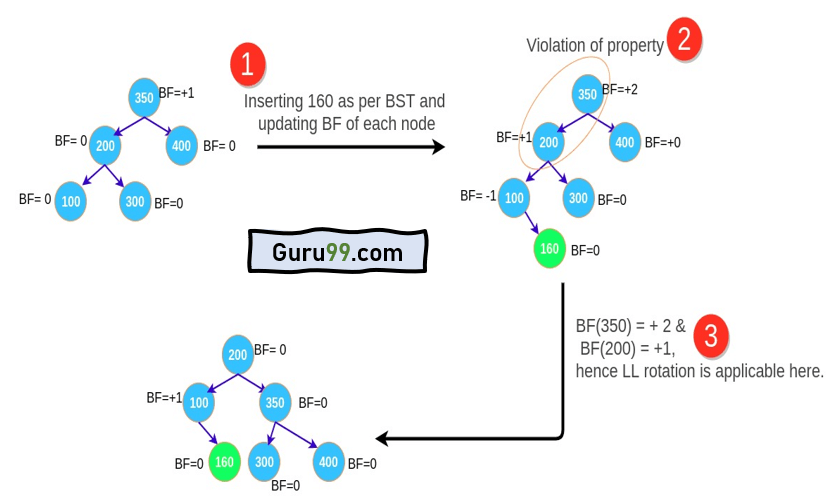
步骤 1:使用BST的相同插入算法将节点插入AVL树。在上面的示例中,插入160。
步骤 2:添加节点后,更新每个节点的平衡因子。插入160后,更新每个节点的平衡因子。
步骤 3:现在检查是否有任何节点违反了平衡因子的范围,如果违反了平衡因子,则使用以下情况执行旋转。在上面的示例中,350的平衡因子被违反,并且情况1适用于那里,我们执行LL旋转,树再次平衡。
- 如果BF(节点) = +2 且 BF(节点 -> 左孩子) = +1,执行LL旋转。
- 如果BF(节点) = -2 且 BF(节点 -> 右孩子) = 1,执行RR旋转。
- 如果BF(节点) = -2 且 BF(节点 -> 右孩子) = +1,执行RL旋转。
- 如果BF(节点) = +2 且 BF(节点 -> 左孩子) = -1,执行LR旋转。
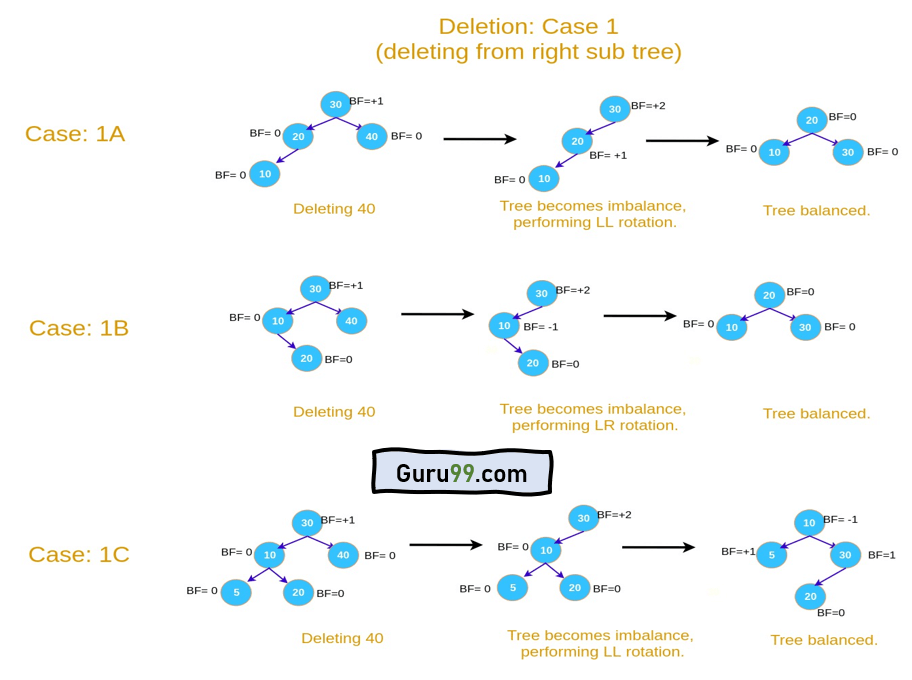
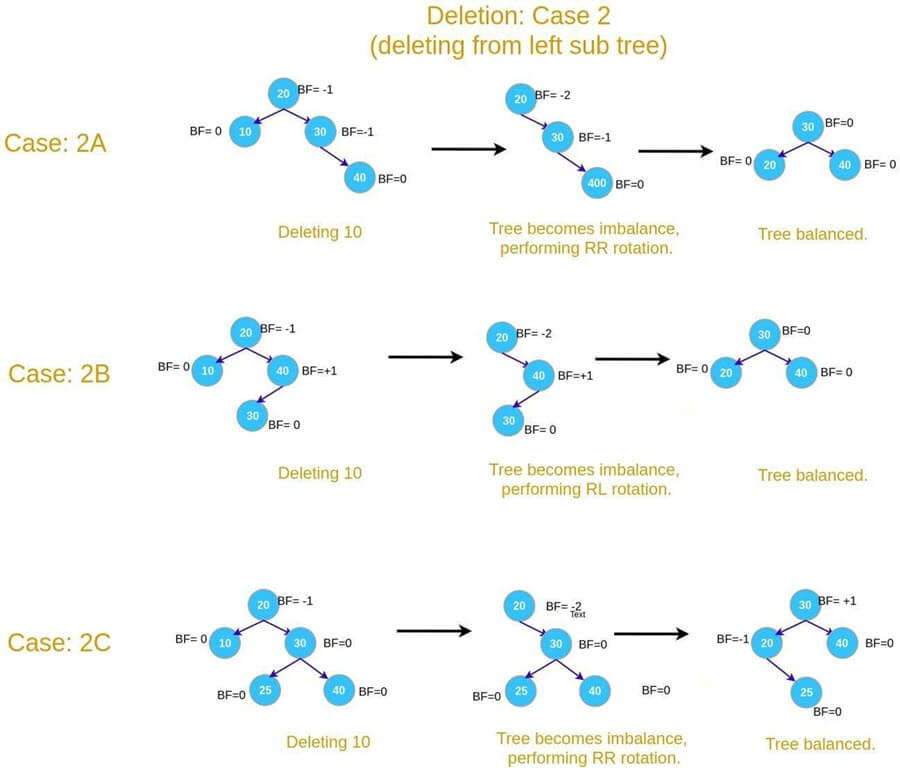
AVL树中的删除
删除操作也非常直接。我们使用与普通二叉搜索树相同的逻辑进行删除。删除后,如果需要,我们会重构树以维持其平衡的高度。
步骤 1:在树中找到元素。
步骤 2:根据BST删除逻辑删除节点。
步骤 3:有两种可能的情况:
情况 1:从右子树删除。
- 1A。如果BF(节点) = +2 且 BF(节点 -> 左孩子) = +1,执行LL旋转。
- 1B。如果BF(节点) = +2 且 BF(节点 -> 左孩子) = -1,执行LR旋转。
- 1C。如果BF(节点) = +2 且 BF(节点 -> 左孩子) = 0,执行LL旋转。
情况 2:从左子树删除。
- 2A。如果BF(节点) = -2 且 BF(节点 -> 右孩子) = -1,执行RR旋转。
- 2B。如果BF(节点) = -2 且 BF(节点 -> 右孩子) = +1,执行RL旋转。
- 2C。如果BF(节点) = -2 且 BF(节点 -> 右孩子) = 0,执行RR旋转。
AVL树的C++示例
下面是实现了AVL树的C++代码
#include <iostream>
#include <queue>
#include <unordered_map>
using namespace std;
struct node {
struct node *left;
int data;
int height;
struct node *right;
};
class AVL
{
private:
public:
struct node * root;
AVL(){
this->root = NULL;
}
int calheight(struct node *p){
if(p->left && p->right){
if (p->left->height < p->right->height)
return p->right->height + 1;
else return p->left->height + 1;
}
else if(p->left && p->right == NULL){
return p->left->height + 1;
}
else if(p->left ==NULL && p->right){
return p->right->height + 1;
}
return 0;
}
int bf(struct node *n){
if(n->left && n->right){
return n->left->height - n->right->height;
}
else if(n->left && n->right == NULL){
return n->left->height;
}
else if(n->left== NULL && n->right ){
return -n->right->height;
}
}
struct node * llrotation(struct node *n){
struct node *p;
struct node *tp;
p = n;
tp = p->left;
p->left = tp->right;
tp->right = p;
return tp;
}
struct node * rrrotation(struct node *n){
struct node *p;
struct node *tp;
p = n;
tp = p->right;
p->right = tp->left;
tp->left = p;
return tp;
}
struct node * rlrotation(struct node *n){
struct node *p;
struct node *tp;
struct node *tp2;
p = n;
tp = p->right;
tp2 =p->right->left;
p -> right = tp2->left;
tp ->left = tp2->right;
tp2 ->left = p;
tp2->right = tp;
return tp2;
}
struct node * lrrotation(struct node *n){
struct node *p;
struct node *tp;
struct node *tp2;
p = n;
tp = p->left;
tp2 =p->left->right;
p -> left = tp2->right;
tp ->right = tp2->left;
tp2 ->right = p;
tp2->left = tp;
return tp2;
}
struct node* insert(struct node *r,int data){
if(r==NULL){
struct node *n;
n = new struct node;
n->data = data;
r = n;
r->left = r->right = NULL;
r->height = 1;
return r;
}
else{
if(data < r->data)
r->left = insert(r->left,data);
else
r->right = insert(r->right,data);
}
r->height = calheight(r);
if(bf(r)==2 && bf(r->left)==1){
r = llrotation(r);
}
else if(bf(r)==-2 && bf(r->right)==-1){
r = rrrotation(r);
}
else if(bf(r)==-2 && bf(r->right)==1){
r = rlrotation(r);
}
else if(bf(r)==2 && bf(r->left)==-1){
r = lrrotation(r);
}
return r;
}
void levelorder_newline(){
if (this->root == NULL){
cout<<"\n"<<"Empty tree"<<"\n";
return;
}
levelorder_newline(this->root);
}
void levelorder_newline(struct node *v){
queue <struct node *> q;
struct node *cur;
q.push(v);
q.push(NULL);
while(!q.empty()){
cur = q.front();
q.pop();
if(cur == NULL && q.size()!=0){
cout<<"\n";
q.push(NULL);
continue;
}
if(cur!=NULL){
cout<<" "<<cur->data;
if (cur->left!=NULL){
q.push(cur->left);
}
if (cur->right!=NULL){
q.push(cur->right);
}
}
}
}
struct node * deleteNode(struct node *p,int data){
if(p->left == NULL && p->right == NULL){
if(p==this->root)
this->root = NULL;
delete p;
return NULL;
}
struct node *t;
struct node *q;
if(p->data < data){
p->right = deleteNode(p->right,data);
}
else if(p->data > data){
p->left = deleteNode(p->left,data);
}
else{
if(p->left != NULL){
q = inpre(p->left);
p->data = q->data;
p->left=deleteNode(p->left,q->data);
}
else{
q = insuc(p->right);
p->data = q->data;
p->right = deleteNode(p->right,q->data);
}
}
if(bf(p)==2 && bf(p->left)==1){ p = llrotation(p); }
else if(bf(p)==2 && bf(p->left)==-1){ p = lrrotation(p); }
else if(bf(p)==2 && bf(p->left)==0){ p = llrotation(p); }
else if(bf(p)==-2 && bf(p->right)==-1){ p = rrrotation(p); }
else if(bf(p)==-2 && bf(p->right)==1){ p = rlrotation(p); }
else if(bf(p)==-2 && bf(p->right)==0){ p = llrotation(p); }
return p;
}
struct node* inpre(struct node* p){
while(p->right!=NULL)
p = p->right;
return p;
}
struct node* insuc(struct node* p){
while(p->left!=NULL)
p = p->left;
return p;
}
~AVL(){
}
};
int main(){
AVL b;
int c,x;
do{
cout<<"\n1.Display levelorder on newline";
cout<<"\n2.Insert";
cout<<"\n3.Delete\n";
cout<<"\n0.Exit\n";
cout<<"\nChoice: ";
cin>>c;
switch (c)
{
case 1:
b.levelorder_newline();
// to print the tree in level order
break;
case 2:
cout<<"\nEnter no. ";
cin>>x;
b.root = b.insert(b.root,x);
break;
case 3:
cout<<"\nWhat to delete? ";
cin>>x;
b.root = b.deleteNode(b.root,x);
break;
case 0:
break;
}
} while(c!=0);
}
上面代码的运行示例
- 复制上面的代码并粘贴到“avl.cpp”中。
- 编译代码
g++ avl.cpp -o run
- 运行代码。
./run
AVL树的优点
- AVL树的高度始终是平衡的。树的高度永远不会超过log N,其中N是树中的节点总数。
- 与普通二叉搜索树相比,它提供了更好的搜索时间复杂度。
- AVL树具有自平衡功能。
摘要
- AVL树是自平衡二叉搜索树。
- 平衡因子是AVL树的基本属性。
- 节点的平衡因子定义为该节点的左子树和右子树高度之差。
- 平衡因子的有效值为-1、0和+1。
- 插入和删除操作在违反平衡因子后需要执行旋转。
- 插入、删除和搜索操作的时间复杂度为O(log N)。
- AVL树遵循二叉搜索树的所有属性。
- 左子树包含小于根节点的节点。右子树包含始终大于根节点的节点。
- AVL树用于插入和删除操作的频率低于搜索操作的场景。