数据结构中图的类型及示例

图是一种非线性数据结构，由顶点和边组成。顶点包含信息或数据，边则作为一对顶点之间的链接。

根据节点和边在图中的位置，图可以有多种类型。以下是一些重要的图的类型：

有向图

有向图的边带有箭头，表示方向。箭头决定了边的指向或终点。

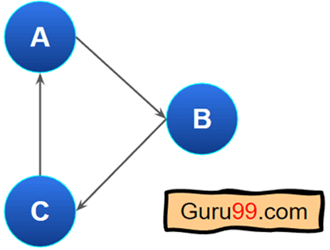
这是一个有向图的例子。

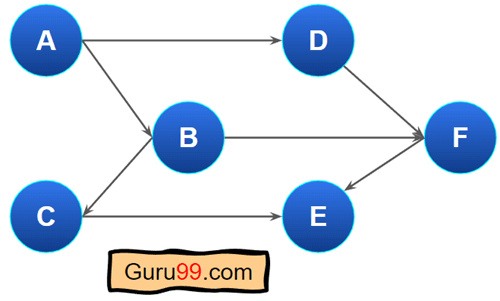
• 我们可以从节点 A 到达 D。
• 然而，由于边只从 A 指向 D，我们不能从 D 到达 A。
• 由于图中没有权重，从顶点 A 到 D 的旅行成本与从 D 到 F 的旅行成本相同。

无向图

无向图的边没有箭头。这意味着我们可以在两个顶点之间双向移动。

这是一个无向图的简单示例。

在上图中，

• 我们可以从 A 移动到 B。
• 我们也可以从 B 移动到 A。
• 边没有方向。

这是一个没有权重的、具有有限数量的顶点和边的无向图的例子。

加权图

边上带有权重或成本的图称为加权图。数值通常代表从一个顶点到另一个顶点的移动成本。有向图和无向图都可以有边的权重。

这是一个加权图（有向）的示例。

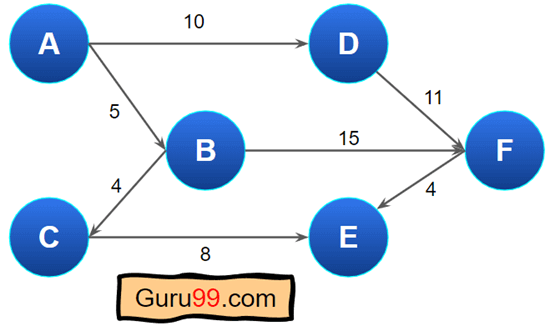
• 从 A 到 B，有一条边，权重为 5，这意味着从 A 到 B 的移动成本是 5。
• A 指向 B，但在该图中，B 没有直接指向 A 的边。因此，我们不能从 B 到 A。
• 但是，如果我们想从 A 到 F，有多个路径。路径是 ADF、ABF。ADF 的成本是 (10+11) 或 21。
• 在这里，ABF 路径的成本是 (5+15) 或 20。这里我们正在将路径中每条边的权重相加。

这是一个带权重的无向图的示例。

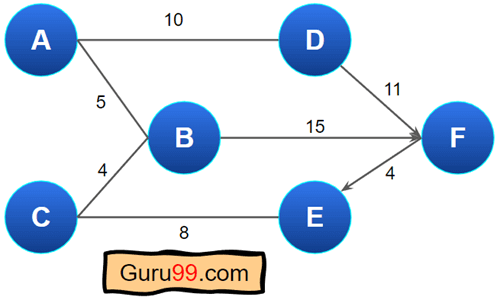
在这里，边有权重但没有方向。所以，这意味着从顶点 A 到 D 的旅行成本是 10，反之亦然。

双向图

双向图和无向图有一个共同的属性。那就是：

• 通常，无向图可以在两个顶点之间有一条边。

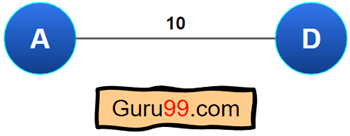
例如

• 在这里，从 A 到 D 或从 D 到 A 的移动成本是 10。
• 在双向图中，我们可以在两个顶点之间有多条边。

这是一个例子。

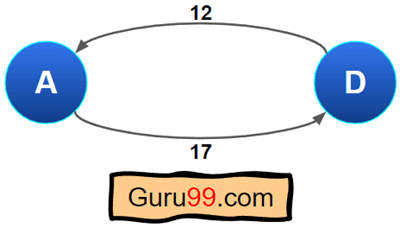
从 A 到 D 的旅行成本是 17，但从 D 到 A 的旅行成本是 12。因此，我们不能为无向图指定两个不同的权重。

无限图

图将包含无限数量的边和节点。如果一个图是无限的，并且它也是一个连通图，那么它也将包含无限数量的边。这里，扩展的边意味着通过边可能有更多的边连接到这些节点。

这是无限图的一个例子。

空图

空图只包含节点或顶点，但没有边。如果给定一个图 G = (V, E)，其中 V 是顶点，E 是边，如果边数 E 为零，则它将是空图。

这是一个空图的例子。

平凡图

如果图数据结构只包含一个顶点或节点，没有边，则该图被认为是平凡图。

这是一个平凡图的例子。

多重图

当两个顶点之间有多条边，或者顶点有自环时，图称为多重图。“自环”在图数据结构中是指指向同一节点或顶点的边。多重图可以是定向的或无定向的。

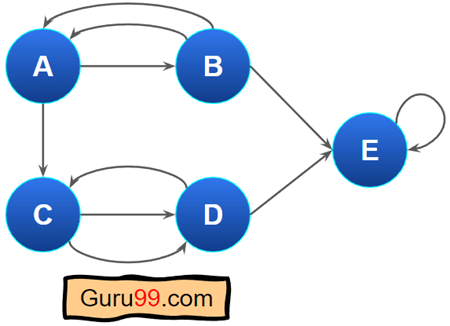
这是一个多重图的例子。

从 B 到 A 有两条边。此外，顶点 E 有一个自环。上面的图是一个没有边权重的有向图。

完全图

如果每个顶点都与其他所有顶点都有有向或无向边，则该图是完全图。

假设总共有 V 个顶点，并且每个顶点都有 V-1 条边。那么，这个图将被称为完全图。在这种类型的图中，每个顶点都通过边连接到所有其他顶点。

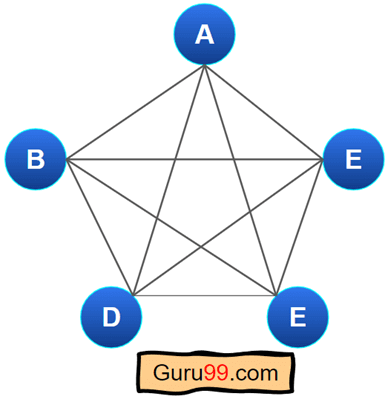
这是一个具有五个顶点的完全图的示例。

您可以看到图中有五个节点，并且所有节点都有四个边。

连通图

如果我们可以从一个节点或顶点开始，并从起始节点遍历所有节点，那么该图就称为连通图。为此，每对节点或顶点之间应该至少有一条边。

这是一个连通图的示例。

以下是对上述“完全图示例”图的一些解释。

• 假设 C 和 F 之间没有边，我们无法从 A 到 G。但是，C 到 F 的边使我们能够从给定节点到达任何节点。
• 完全图是连通图，因为我们可以从一个节点移动到给定图中的任何其他节点。

有环图

如果图中存在一个或多个环，则该图称为有环图。

这是一个有环图的示例。

在这里，顶点 A、B 和 C 构成一个环。

一个图可以有多个环。

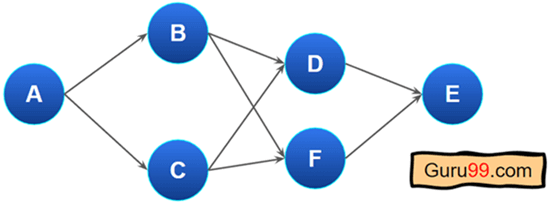
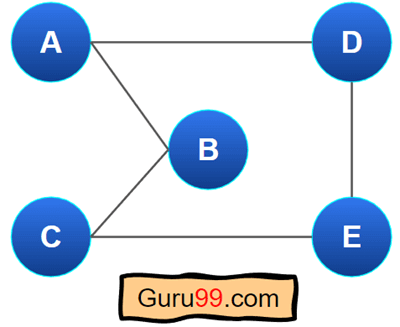
有向无环图（DAG）

如果图中没有环，则该图称为有向无环图或 DAG。DAG 在进行 拓扑排序 或查找执行顺序时很重要。DAG 在创建调度系统或扫描资源依赖性等方面也很重要。但是，上面的图不包含任何内部环。

这是一个有向无环图（DAG）的简单示例。

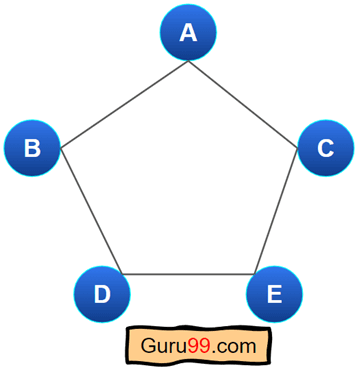
环图

环图与有环图不同。在环图中，每个节点将精确连接两个边，这意味着每个节点的度数都将是精确的两个。

这是一个环图的示例。

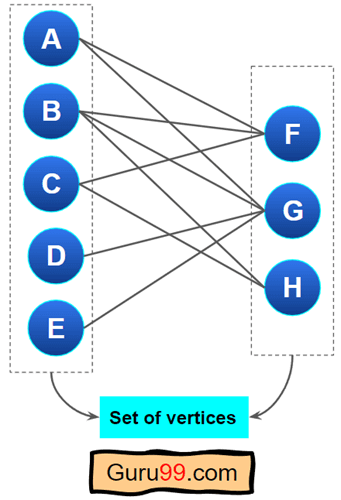
二分图

这类 图 是特殊的图，其中顶点被分配给两个集合。

二分图必须遵循规则：

• 两个顶点集必须是独立的，这意味着所有顶点必须分成两组或集合。
• 同一集合的顶点不应形成任何边。

欧拉图

如果所有顶点的度数都是偶数，则图数据结构被视为欧拉图。顶点度数是指指向或从特定顶点发出的边的数量。

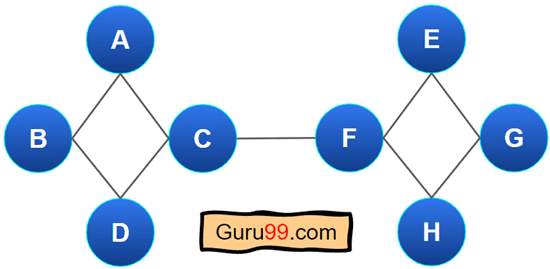
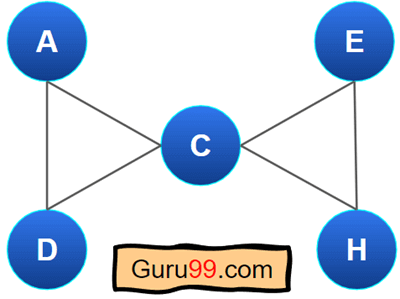
这是一个欧拉图的示例。

所有顶点的度数都是偶数。顶点 A、D、E 和 H 的度数为 2。节点 C 的度数为 4，是偶数。

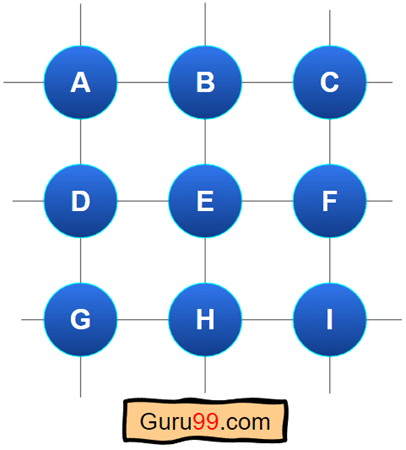
哈密顿图

哈密顿图是一个连通图，您可以从给定顶点访问所有顶点，而无需重访同一节点或使用同一条边。这种连通图称为“哈密顿图”。用于验证给定图是否为哈密顿图的路径称为哈密顿路径。

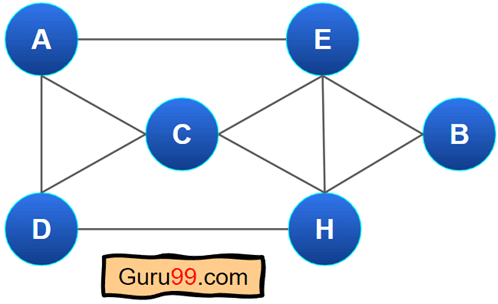
这是一个哈密顿图的简单示例。

在此图中，我们可以从任何节点访问图中的所有顶点。其中一条路径可以是 **A-D-C-H-B-E**。也可以找到哈密顿环。哈密顿环从同一顶点开始和结束。因此，哈密顿环将是 **A-D-C-H-B-E-A**。