图数据结构和算法 (示例)

什么是数据结构中的图？

图是一种非线性数据结构，由顶点和边组成，其中顶点包含信息或数据，边充当一对顶点之间的链接。

它用于解决现实世界的问题，例如寻找到达目的地位置的最佳路线以及电信和社交网络的路线。用户被视为图中的一个节点，电线是连接用户的边。

如果边表示为 E，顶点表示为 V，则图 G 可以表示为顶点和边的集合，例如 G (V, E)

数据结构中图的示例

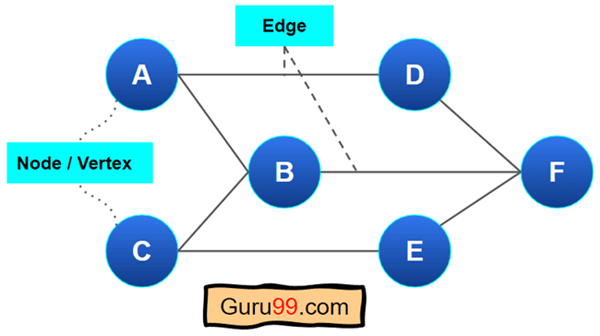
这是一个简单的数据结构图示例

这是一个简单的无向图（一种图）。这里的顶点集是：{A、B、C、D、E、F}。两个顶点构成一条边。例如，A 和 B 通过一条边连接。但是，A 和 F 没有任何边连接。

数据结构中的图术语

以下是图数据结构中使用的一些重要术语

术语	描述
顶点	所有数据元素都称为顶点或节点。在上图中，A、B、C、D 和 E 是顶点。
边 (弧)	连接两个节点或顶点的连接线称为边（弧）。它有两个端点，表示为（起始顶点，结束顶点）。
无向边	它是双向边。
有向边	它是单向边。
加权边	带有值的边。
度	在图中，连接到顶点的边的数量称为度。
入度	连接到顶点的入边总数。
出度	连接到顶点的出边总数。
自环	如果一条边的两个端点重合，则称该边为自环。
邻接	如果边连接，则称顶点是相邻的。

数据结构中图的类型

以下是数据结构中最常见的图类型列表

• 有向图
• 无向图
• 加权图
• 双向图
• 无限图
• 空图
• 平凡图
• 多重图
• 完全图
• 连通图
• 有环图
• 有向无环图 (DAG)
• 循环图
• 二分图
• 欧拉图
• 哈密顿图

图数据结构的应用程序

图有很多用例。有很多算法大量使用图。以下是一些图的应用

• 谷歌地图使用图来查找两条道路的交叉点并计算两个位置之间的距离。
  例如，Dijkstra 算法用于查找源位置和目标位置之间的最短距离。
• Facebook 使用图来查找用户的共同好友。其算法将每个用户视为图的一个节点。
• 对于资源分配，使用 DAG（有向无环图）。它检查资源的依赖性。
• Google 搜索引擎使用图来创建网站排名。
• 导航设备使用图数据结构。
• 路由器及其协议使用图来学习目标路径。