图的邻接表和邻接矩阵表示法
虽然它们看起来不同,但所有 类型的图 都可以用类似的方式表示。通常有两种图表示方法:
- 邻接矩阵
- 邻接表
邻接表
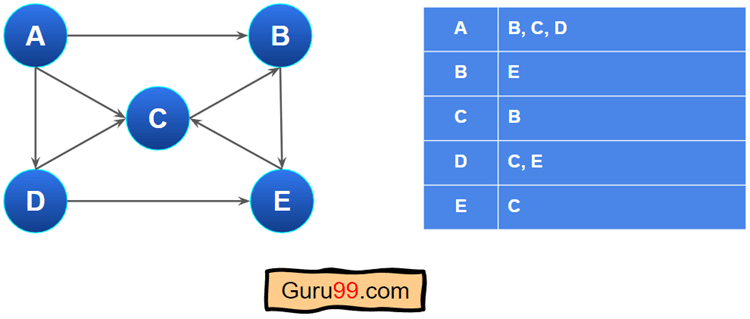
邻接表由链表组成。每个顶点被视为一个数组索引,每个元素代表一个链表。这些链表包含与索引顶点有边的顶点。
这是一个邻接表的示例
假设一个图包含 V 个顶点和 E 条边。
通常,空间复杂度为 O(V + E)。
如果给定的图是完全图,则最坏情况下的空间复杂度为 O(V^2)。
邻接矩阵
邻接矩阵由一个二维数组组成。对于拥有 V 个顶点的图,矩阵的大小将是 VxV。
例如,matrix[i][j] = 5。这意味着节点 i 和 j 之间存在一条权重为 5 的边。
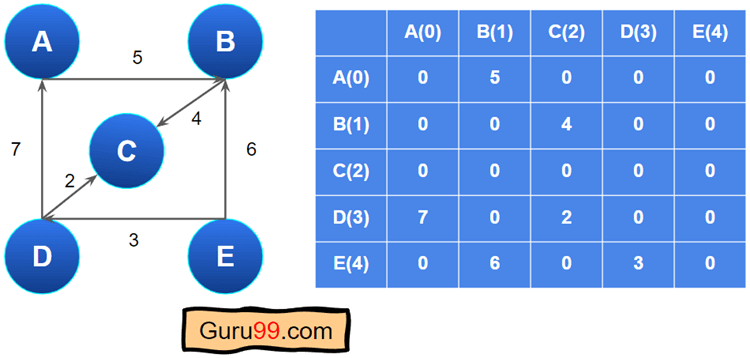
让我们看一下下面的图及其邻接矩阵
我们按照以下步骤使用 二维数组 创建了它
步骤 1) 顶点 A 与 B 有直接边,权重为 5。因此,A 行 B 列的单元格将填入 5。A 行的其余单元格将填入零。
步骤 2) 顶点 B 与 C 有直接边,权重为 4。因此,B 行 C 列的单元格将填入 4。B 行的其余单元格将填入零,因为 B 没有指向其他节点的出边。
步骤 3) 顶点 C 没有直接指向任何其他顶点的边。因此,C 行将填入零。
步骤 4) 顶点 D 与 A 和 C 有有向边。
- 在这里,D 行 A 列的单元格将具有值 7。D 行 C 列的单元格将具有值 2。
- D 行的其余单元格将填入零。
步骤 5) 顶点 E 与 B 和 D 有有向边。E 行 B 列的单元格将具有值 6。E 行 D 列的单元格将具有值 3。D 行的其余单元格将填入零。
以下是一些需要注意的点
- 当邻接矩阵的主对角线为 0 时,图没有自环。
- 如果索引 (a,b) 和 (b,a) 的值不相同,则该图是无向图。否则,该图是无向图。
- 如果单元格的值大于 1,则该图是有权图。
邻接矩阵存在一些问题,因为它需要平方空间。在这里,我们存储了未连接的边。这些边分配了内存空间。
例如,如果我们有一个包含 100 个节点的图,则需要一万个单元格来将其存储在 RAM 中。如果图中的边很少,分配如此大的内存可能会浪费。因此,使用邻接矩阵的空间复杂度将是 O(N^2),其中 N 表示图中的节点数。