汉诺塔算法:Python、C++ 代码
什么是汉诺塔?
汉诺塔是一个数学谜题,包含三根柱子和数量不等的圆盘,圆盘一个叠在一个上面。它也被称为婆罗门塔或卢卡斯塔,因为法国数学家爱德华·卢卡斯在1883年引入了它。这个谜题基于在三根柱子之间移动金盘的传说。
这个谜题有三根柱子和数量不等的堆叠圆盘。这些柱子设计成循环塔。因此,直径较大的圆盘堆叠在底部,较小的圆盘堆叠在顶部。
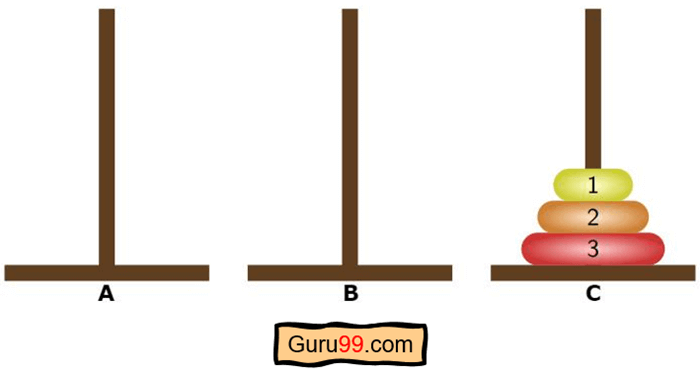
最初,我们有三根钉子或柱子。其中一根(示例中显示为A)堆叠了所有圆盘。我们的目标是通过遵守一些特定的规则,将整个圆盘堆从一根柱子(A)移动到另一根(C)。
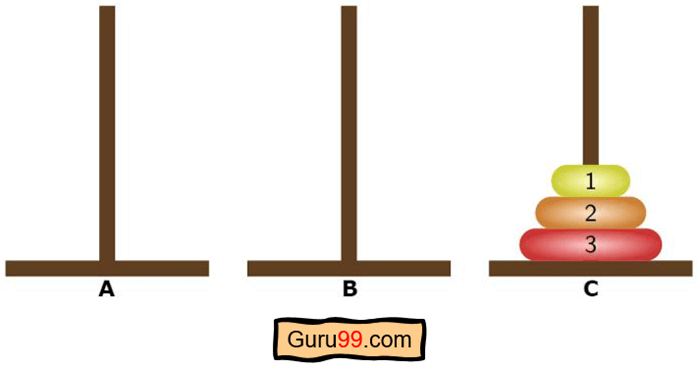
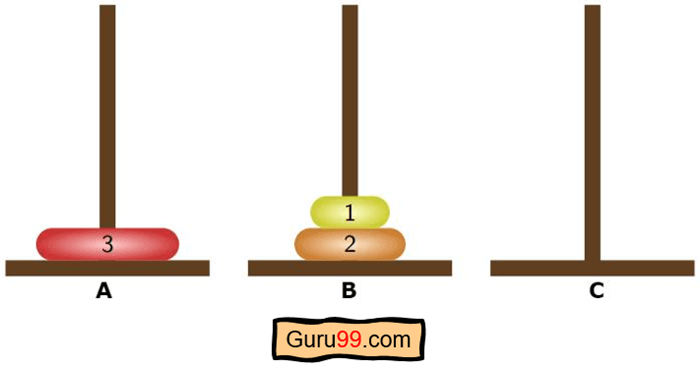
这是谜题的初始设置-
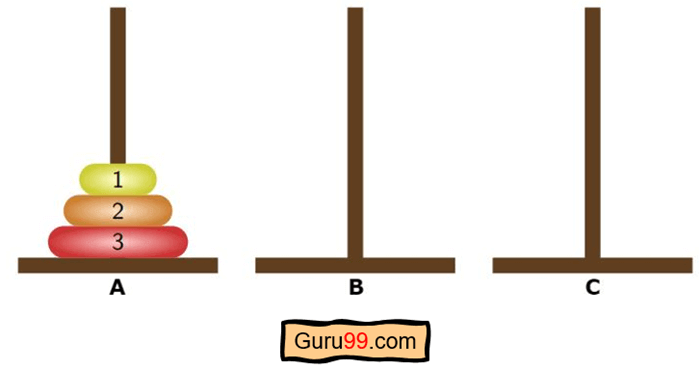
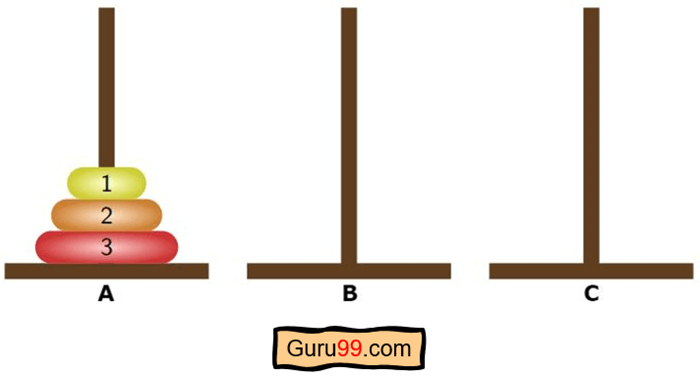
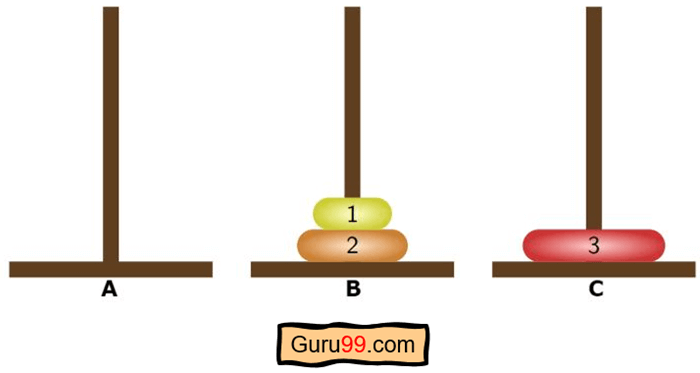
这是最终目标-
汉诺塔规则
以下是汉诺塔的一些重要规则
- 这个谜题的初始状态是,所有圆盘都将堆叠在第一根柱子上。
- 最终状态是将第一根柱子上的所有圆盘堆叠在第二根或第三根柱子上。
- 我们可以在任何时候将一个圆盘从一根柱子移动到另一根柱子。
- 我们只能移动柱子最上面的圆盘。
- 圆盘不能放在比它小的圆盘上面。
最初的传说涉及移动64个圆盘。祭司们可以根据规则一次移动一个圆盘。根据传说,有一个预言说,如果他们完成这项工作,世界将会毁灭。在时间复杂度部分,我们将展示一个有n个圆盘的汉诺塔需要2^n – 1次移动。
所以,如果祭司们需要1秒钟来移动圆盘,那么他们需要花费的总时间将是2^64 – 1秒,或者584,942,417,356年,26天,7小时和15秒。
汉诺塔算法
解决汉诺塔的一种通用方法是递归算法。首先,我们需要决定两个柱子或钉子作为源和目标,而备用的柱子将是辅助的或帮助的。
以下是解决汉诺塔谜题的步骤
- 将顶部的 n-1 个圆盘从源柱移动到辅助柱。
- 之后,将第 n 个圆盘从源柱移动到目标柱。
- 最后,将剩余的 n-1 个圆盘从辅助柱移动到目标柱。
注意:如果我们只有一个圆盘,我们可以直接将其从源移动到目标。
如何解决汉诺塔谜题
让我们以三个圆盘为例来说明算法,并将 A 柱视为源,B 柱视为辅助,C 柱视为目标。
步骤 1) 最初,所有圆盘都堆叠在 A 柱上。
此时
源 = A 柱
目标 = C 柱
辅助 = B 柱
现在,我们需要将顶部的 n-1 个圆盘从源移动到辅助。
注意:虽然我们一次只能移动一个圆盘,但这会将我们的问题从一个3圆盘问题分解为一个2圆盘问题,这是一个递归调用。
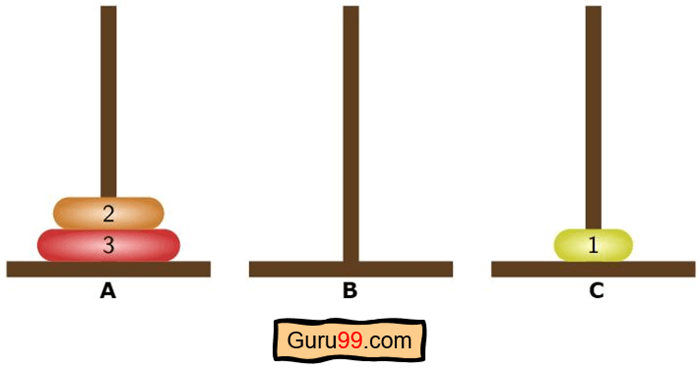
步骤 2) 当我们从 A 柱调用递归调用,目标是 B 柱时,我们将使用 C 柱作为辅助。
请注意,对于同样的汉诺塔问题,我们现在又回到了两个圆盘的初始阶段。
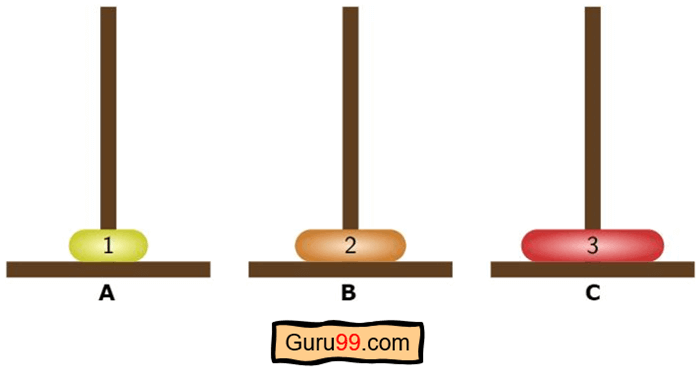
现在我们需要将 n-1 个或一个圆盘从源移动到辅助,将最小的圆盘从 A 柱移动到 C 柱。
此时
源 = A 柱
目标 = B 柱
辅助 = C 柱
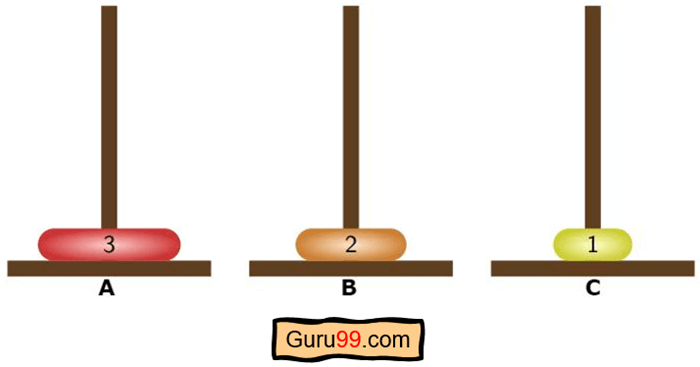
步骤 3) 然后,根据我们的算法,第 n 个或第 2 个圆盘应该被转移到目标柱或 B 柱。
此时
源 = A 柱
目标 = B 柱
辅助 = C 柱
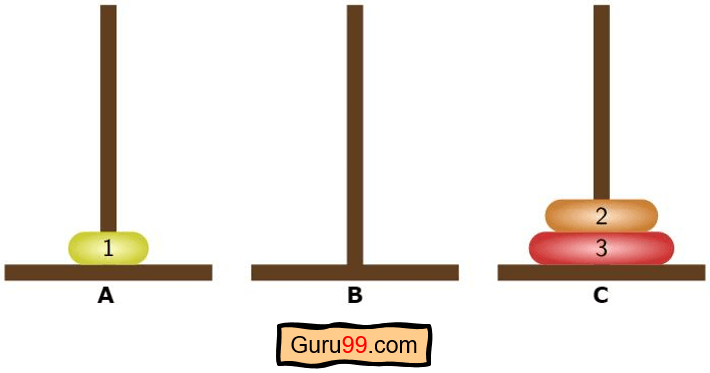
步骤 4) 现在,根据我们算法的第三阶段,我们将把 n-1 个圆盘或第 1 个圆盘从辅助柱或 C 柱移动到目标柱或 B 柱。
此时
源 = A 柱
目标 = B 柱
辅助 = C 柱
步骤 5) 完成递归调用后,我们将返回到我们之前设置的算法第一阶段。
步骤 6) 现在,在第二阶段,我们将把源柱移动到目标柱,也就是将第 3 个圆盘从 A 柱移动到 C 柱。
此时
源 = A 柱
目标 = C 柱
辅助 = B 柱
步骤 7) 现在我们可以看到
d 是将剩余的圆盘从辅助柱(B 柱)移动到目标柱(C 柱)。在这种情况下,我们将使用初始的源柱或 A 柱作为辅助。
步骤 8) 由于我们不能同时移动两个圆盘,我们将为第 1 个圆盘调用递归调用。根据最后一步和我们的算法,这一步的目标是 A 柱。
此时
源 = B 柱
目标 = A 柱
辅助 = C 柱
步骤 9) 我们的递归调用现在已经完成。然后我们将第 2 个圆盘从其源移动到其目标。
此时
源 = B 柱
目标 = C 柱
辅助 = A 柱
步骤 10) 然后我们将剩余的 n-1 个或第 1 个圆盘从辅助柱移动到目标柱。
此时
源 = A 柱
目标 = C 柱
辅助 = B 柱
汉诺塔的伪代码
START
Procedure Tower_Of_Hanoi(disk, source, dest, helper)
IF disk == 1, THEN
move disk from source to dest
ELSE
Tower_Of_Hanoi (disk - 1, source, helper, dest)
move disk from source to dest
Tower_Of_Hanoi (disk - 1, helper, dest, source)
END IF
END Procedure
C++ 中的程序代码
#include <bits/stdc++.h>
using namespace std;
void tower_of_hanoi(int num, string source, string dest, string helper) {
if (num == 1) {
cout << " Move disk 1 from tower " << source << " to tower " << dest << endl;
return;
}
tower_of_hanoi(num - 1, source, helper, dest);
cout << " Move disk " << num << " from tower " << source << " to tower " << dest << endl;
tower_of_hanoi(num - 1, helper, dest, source);
}
int main() {
int num;
cin >> num;
printf("The sequence of moves :\n");
tower_of_hanoi(num, "I", "III", "II");
return 0;
}
输出
3 The sequence of moves : Move disk 1 from tower I to tower III Move disk 2 from tower I to tower II Move disk 1 from tower III to tower II Move disk 3 from tower I to tower III Move disk 1 from tower II to tower I Move disk 2 from tower II to tower III Move disk 1 from tower I to tower III
Python 中的程序代码
def tower_of_hanoi(n, source, destination, helper):
if n==1:
print ("Move disk 1 from peg", source," to peg", destination)
return
tower_of_hanoi(n-1, source, helper, destination)
print ("Move disk",n," from peg", source," to peg", destination)
tower_of_hanoi(n-1, helper, destination, source)
# n = number of disks
n = 3
tower_of_hanoi(n,' A','B','C')
输出
Move disk 1 from peg A to peg B Move disk 2 from peg A to peg C Move disk 1 from peg B to peg C Move disk 3 from peg A to peg B Move disk 1 from peg C to peg A Move disk 2 from peg C to peg B Move disk 1 from peg A to peg B
汉诺塔的复杂度
以下是汉诺塔的时间和空间复杂度
1) 时间复杂度
如果我们回顾我们的算法,我们可以看到我们对 (n-1) 个圆盘的递归调用执行了两次。这些对 (n-1) 个圆盘的递归调用可以分解为 ((n-1)-1) 等等,直到我们只剩下一个圆盘需要移动。
对于三个圆盘-
- 第 3 个圆盘调用两次关于第 2 个圆盘的递归函数。
- 第 2 个圆盘调用两次关于第 1 个圆盘的递归函数。
- 第 1 个圆盘可以在常数时间内移动,而解决 3 个圆盘需要的时间。
= 2 * (解决 2 个圆盘所需时间) + 移动第 3 个圆盘的常数时间
= 2 * (2 * 解决 1 个圆盘所需时间 + 移动第 2 个圆盘的常数时间) + 移动第 3 个圆盘的常数时间
= (2*2) * (移动第 1 个圆盘的常数时间) + 2 * 移动第 2 个圆盘的常数时间 + 移动第 3 个圆盘的常数时间
对于 n 个圆盘,可以写成 –
(2n-1 * 移动第 1 个圆盘的常数时间 + 2n-2 * 移动第 2 个圆盘的常数时间 + …。
这个几何级数的结果是 O(2n-1) 或 O(2n),这是指数级的。
2) 空间复杂度
汉诺塔的空间复杂度是 O(n)。这是因为我们需要存储圆盘的顺序。当我们使用递归时,它会使用堆栈。堆栈的最大大小可以是“n”。这就是为什么空间复杂度变成 O(n) 的原因。