旅行商问题：Python、C++ 算法

什么是旅行推销员问题 (TSP)？

旅行推销员问题 (TSP) 是计算机科学理论中的一个经典组合数学问题。该问题要求在图中找到最短路径，条件是每个节点只访问一次，并返回出发城市。

问题陈述给出了一系列城市以及每对城市之间的距离。

目标：从起始城市出发，每个城市只访问一次，然后返回起始城市。我们的目标是找到完成环程的最短可能路径。

TSP 示例

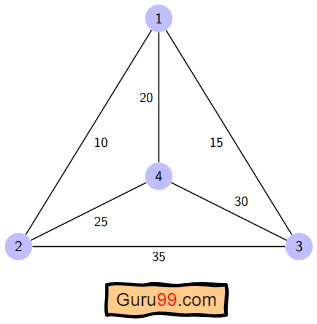
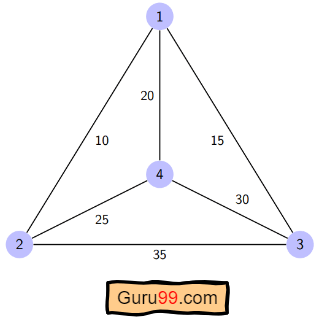
这里给出了一个图，其中 1、2、3 和 4 代表城市，与每条边相关联的权重代表这些城市之间的距离。

目标是找到最短可能的行程路径，该路径从起始城市开始，仅访问其他城市或节点一次，然后返回起始城市。

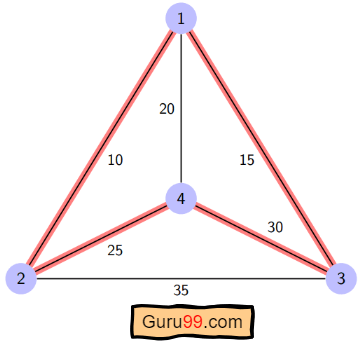
对于上述图形，最优路线是遵循最短成本路径：1-2-4-3-1。这条最短路线的成本为 10+25+30+15 = 80

旅行推销员问题的不同解决方案

旅行推销员问题 (TSP) 被归类为 NP-hard 问题，因为它没有多项式时间算法。随着城市数量的增加，复杂度呈指数级增长。

有多种方法可以解决旅行推销员问题 (tsp)。一些流行的解决方案是：

穷举法是最朴素的解决旅行推销员问题的方法。在这种方法中，我们首先计算所有可能的路径，然后进行比较。由 n 个城市组成的图中的路径数量为 n!。以这种穷举法解决旅行推销员问题在计算上非常昂贵。

分支定界法：在此方法中，问题被分解为子问题。这些单独子问题的解决方案将提供最优解。

本教程将演示一种动态规划方法，即分支定界法的递归版本，来解决旅行推销员问题。

动态规划是一种通过分析所有可能的路径来寻求最优解的方法。它是解决旅行推销员问题的精确解法之一，其成本比提供近似最优解的贪心算法要高。

该方法的计算复杂度为 O(N^2 * 2^N)，稍后将在本文中讨论。

最近邻方法是一种基于启发式贪心算法的方法，我们选择最近的邻居节点。这种方法比动态方法计算成本更低。但它不能保证最优解。此方法用于近似最优解。

旅行推销员问题算法

我们将使用动态规划方法来解决旅行推销员问题 (TSP)。

在开始算法之前，让我们熟悉一些术语。

图 G=(V, E)，它是顶点和边的集合。
V 是顶点的集合。
E 是边的集合。
顶点通过边连接。
Dist(i,j) 表示两个顶点 i 和 j 之间的非负距离。

假设 S 是城市的一个子集，属于 {1, 2, 3, …, n}，其中 1, 2, 3…n 是城市，i, j 是该子集中的两个城市。现在 cost(i, S, j) 的定义方式是访问 S 中的节点的最短路径的长度，恰好只访问一次，并且起始点和结束点分别为 i 和 j。

例如，cost (1, {2, 3, 4}, 1) 表示最短路径的长度，其中

起始城市是 1
城市 2、3 和 4 只访问一次
结束点是 1

动态规划算法如下：

设置 cost(i, , i) = 0，表示我们在 i 开始并在 i 结束，成本为 0。
当 |S| > 1 时，我们将 cost(i, S, 1) 定义为 ∝，其中 i !=1。因为一开始，我们不知道从城市 i 到城市 1 的确切成本。
现在，我们需要从 1 开始并完成行程。我们需要选择下一个城市，方式如下：

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j)，其中 i∈S 且 i≠j

对于给定的图形，邻接矩阵将是下面的

dist(i,j)	1	2	3	4
1	0	10	15	20
2	10	0	35	25
3	15	35	0	30
4	20	25	30	0

让我们看看我们的算法是如何工作的

步骤 1) 我们将旅程视为从城市 1 开始，访问其他城市一次，然后返回城市 1。

步骤 2) S 是城市的子集。根据我们的算法，对于所有 |S| > 1，我们将距离 cost(i, S, 1) 设置为 ∝。这里的 cost(i, S, j) 表示我们从城市 i 开始，经过城市 3、4，然后到达 1。我们将此路径成本设置为无穷大，因为我们还不知道距离。所以值将是：

Cost (2, {3, 4}, 1) = ∝；这个符号表示我们从城市 2 开始，经过城市 3、4，然后到达 1。并且路径成本是无穷大。同样：

cost(3, {2, 4}, 1) = ∝

cost(4, {2, 3}, 1) = ∝

步骤 3) 现在，对于 S 的所有子集，我们需要找到以下内容：

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j)，其中 j∈S 且 i≠j

这意味着从 i 开始，经过城市子集一次，然后返回城市 j 的最短成本路径。考虑到旅程从城市 1 开始，最优路径成本将是 = cost(1, {其他城市}, 1)。

让我们找出如何实现这一点

现在 S = {1, 2, 3, 4}。有四个元素。因此，子集的数量将是 2^4 或 16。这些子集是：

1) |S| = Null

{Φ}

2) |S| = 1

{{1}, {2}, {3}, {4}}

3) |S| = 2

{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}

4) |S| = 3

{{1, 2, 3}, {1, 2, 4}, {2, 3, 4}, {1, 3, 4}}

5) |S| = 4

由于我们从 1 开始，我们可以丢弃包含城市 1 的子集。

算法计算

1) |S| = Φ

cost (2, Φ, 1) = dist(2, 1) = 10

cost (3, Φ, 1) = dist(3, 1) = 15

cost (4, Φ, 1) = dist(4, 1) = 20

2) |S| = 1

cost (2, {3}, 1) = dist(2, 3) + cost (3, Φ, 1) = 35+15 = 50

cost (2, {4}, 1) = dist(2, 4) + cost (4, Φ, 1) = 25+20 = 45

cost (3, {2}, 1) = dist(3, 2) + cost (2, Φ, 1) = 35+10 = 45

cost (3, {4}, 1) = dist(3, 4) + cost (4, Φ, 1) = 30+20 = 50

cost (4, {2}, 1) = dist(4, 2) + cost (2, Φ, 1) = 25+10 = 35

cost (4, {3}, 1) = dist(4, 3) + cost (3, Φ, 1) = 30+15 = 45

3) |S| = 2

cost (2, {3, 4}, 1) = min [ dist[2,3]+Cost(3,{4},1) = 35+50 = 85,

dist[2,4]+Cost(4,{3},1) = 25+45 = 70 ] = 70

cost (3, {2, 4}, 1) = min [ dist[3,2]+Cost(2,{4},1) = 35+45 = 80,

dist[3,4]+Cost(4,{2},1) = 30+35 = 65 ] = 65

cost (4, {2, 3}, 1) = min [ dist[4,2]+Cost(2,{3},1) = 25+50 = 75

dist[4,3]+Cost(3,{2},1) = 30+45 = 75 ] = 75

4) |S| = 3

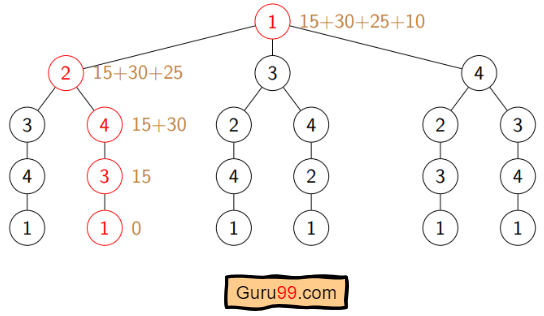
cost (1, {2, 3, 4}, 1) = min [ dist[1,2]+Cost(2,{3,4},1) = 10+70 = 80

dist[1,3]+Cost(3,{2,4},1) = 15+65 = 80

dist[1,4]+Cost(4,{2,3},1) = 20+75 = 95 ] = 80

因此，最优解是 1-2-4-3-1

伪代码

Algorithm: Traveling-Salesman-Problem 
Cost (1, {}, 1) = 0 
for s = 2 to n do 
   for all subsets S belongs to {1, 2, 3, … , n} of size s 
      Cost (s, S, 1) = Infinity
   for all i Є S and i ≠ 1 
      Cost (i, S, j) = min {Cost (i, S – {i}, j) + dist(i, j) for j Є S and i ≠ j} 
Return min(i) Cost (i, {1, 2, 3, …, n}, j) + d(j, i)

C/C++ 实现

这是 C++ 中的实现：C++

#include <bits/stdc++.h>
using namespace std;
#define V 4
#define MAX 1000000
int tsp(int graph[][V], int s)
{
    vector<int> vertex;
    for (int i = 0; i < V; i++)
        if (i != s)
            vertex.push_back(i);
    int min_cost = MAX;
    while(next_permutation(vertex.begin(), vertex.end()))
     {
        int current_cost = 0;
        int j = s;
        for (int i = 0; i < vertex.size(); i++) {
            current_cost += graph[j][vertex[i]];
            j = vertex[i];
        }
        current_cost += graph[j][s];
        min_cost = min(min_cost, current_cost);
        return min_cost;
	}
}
int main()
{
    int graph[][V] = { { 0, 10, 15, 20 },{ 10, 0, 35, 25 },{ 15, 35, 0, 30 },{ 20, 25, 30, 0 } };                      
    int s = 0;
    cout << tsp(graph, s) << endl;
    return 0;
}

输出

Python 实现

from sys import maxsize
from itertools, import permutations
V = 4
def tsp(graph, s):
	vertex = []
	for i in range(V):
		if i != s:
			vertex.append(i)
    min_cost = maxsize
	next_permutation=permutations(vertex)
	for i in next_permutation:
		current_cost = 0
		k = s
		for j in i:
			current_cost += graph[k][j]
			k = j
		current_cost += graph[k][s]
		min_cost = min(min_cost, current_cost)
		return min_cost
graph = [[0, 10, 15, 20], [10, 0, 35, 25], [15, 35, 0, 30], [20, 25, 30, 0]]
		s = 0
print(tsp(graph, s))

输出

TSP 的学术解决方案

计算机科学家们花费了数年时间寻找旅行推销员问题的改进多项式时间算法。到目前为止，该问题仍然是 NP-hard。

尽管最近几年发布了一些解决方案，在一定程度上降低了复杂度。

经典的对称 TSP 由零后缀法解决。
基于生物地理学的优化算法基于迁移策略来解决可以计划为 TSP 的优化问题。
多目标进化算法是为解决基于 NSGA-II 的多个 TSP 而设计的。
多代理系统解决了具有固定资源的 N 个城市的 TSP。

旅行推销员问题的应用

旅行推销员问题 (TSP) 以其最纯粹和修改后的形式应用于现实世界。其中一些是：

规划、物流和制造微芯片：芯片插入问题自然出现在微芯片行业中。这些问题可以计划为旅行推销员问题。
DNA 测序：旅行推销员问题的轻微修改可用于 DNA 测序。在这里，城市代表 DNA 片段，距离代表两个 DNA 片段之间的相似度度量。
天文学：天文学家应用旅行推销员问题来最小化观察各种源所花费的时间。
最优控制问题：旅行推销员问题公式可以应用于最优控制问题。可能需要添加其他一些约束。

TSP 复杂度分析

时间复杂度：每个节点共有 2^N个子问题。所以子问题的总数为 N*2^N。每个子问题都需要线性时间来解决。如果未指定起始节点，我们必须为 N 个节点运行循环。
因此，最优解的总时间复杂度是节点数 * 子问题数 * 解决每个子问题的时间。时间复杂度可以定义为 O(N² * 2^N)。
空间复杂度：动态规划方法使用内存来存储 C(S, i)，其中 S 是顶点集的一个子集。每个节点共有 2^N个子集。所以，空间复杂度为 O(2^N)。

接下来，您将了解埃拉托斯特尼筛法算法