埃拉托斯特尼筛法算法：Python、C++ 示例

埃拉托斯特尼筛法是最简单的素数筛法。它是一种用于在给定限制内搜索所有素数的素数算法。有几种素数筛法。例如——埃拉托斯特尼筛法、阿特金筛法、桑达拉姆筛法等。

“sieve”一词的意思是过滤物质的器具。因此，Python 和其他语言中的筛法算法是指用于筛选素数的算法。

该算法以迭代方式筛选素数。筛选过程从最小的素数开始。素数是大于1且只有两个除数（即1和数字本身）的自然数。非素数被称为合数。

在埃拉托斯特尼筛法中，首先选择一个小的素数，然后过滤掉它所有的倍数。该过程在一个给定的范围内循环进行。

例如

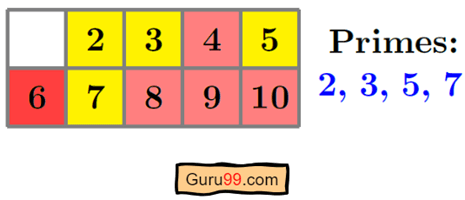
我们以 2 到 10 的数字范围为例。

应用埃拉托斯特尼筛法后，它将生成素数列表 2、3、5、7。

算法埃拉托斯特尼筛法

这是埃拉托斯特尼筛法的算法

步骤 1) 从 2 到给定范围 n 创建一个数字列表。我们从 2 开始，因为它是最小的第一个素数。

步骤 2) 选择列表中的最小数字 x（最初 x 等于 2），遍历列表，通过标记所有选定数字的倍数来过滤相应的合数。

步骤 3) 然后选择下一个素数或列表中的下一个未标记的最小数字，重复步骤 2。

步骤 4) 重复上一步，直到 x 的值小于或等于 n 的平方根（x<=).

注意： 数学原理非常简单。数字范围 n 可以分解为：

n=a*b

再次，n =*

= （小于的因子) * （大于的因子)

所以至少一个素数因子或两者都必须 <=因此，遍历到就足够了。

步骤 5) 完成这四个步骤后，剩下的未标记数字将是该给定范围 n 内的所有素数。

示例

让我们举个例子，看看它是如何工作的。

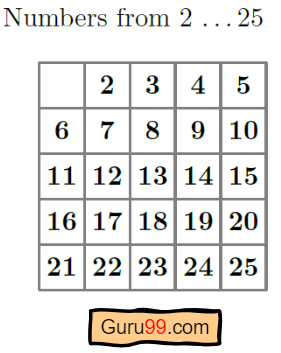
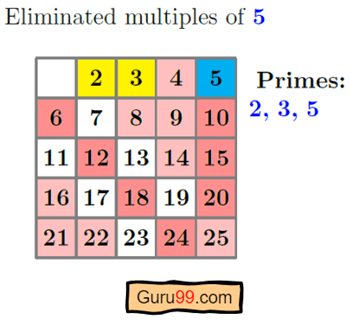
在这个例子中，我们将找到从 2 到 25 的素数列表。所以，n=25。

步骤 1) 在第一步中，我们将取一个从 2 到 25 的数字列表，因为我们选择了 n=25。

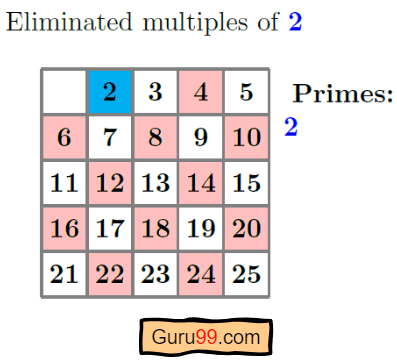
步骤 2) 然后我们选择列表中的最小数字 x。最初 x=2，因为它是最小的素数。然后我们遍历列表并标记 2 的倍数。

给定 n 值的 2 的倍数是：4、6、8、10、12、14、16、18、20、22、24。

注意： 蓝色表示选定的数字，粉色表示被排除的倍数。

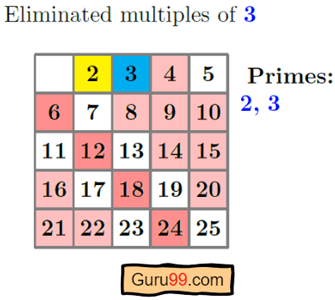
步骤 3) 然后我们选择下一个最小的未标记数字，即 3，并通过标记 3 的倍数重复上一步。

步骤 4) 我们以相同的方式重复步骤 3，直到 x=或 5。

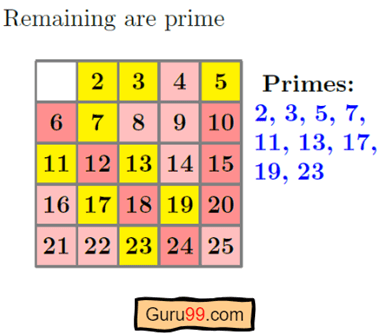
步骤 5) 剩余的未标记数字将是从 2 到 25 的素数。

伪代码

Begin
	Declare a boolean array of size n and initialize it to true
	For all numbers i : from 2 to sqrt(n)
     		IF bool value of i is true THEN
         			i is prime
         			For all multiples of i (i<n)
             			mark multiples of i as composite
Print all unmarked numbers
End

埃拉托斯特尼筛法 C/C++ 代码示例

#include <iostream>
#include <cstring>
using namespace std;
void Sieve_Of_Eratosthenes(int n)
{
    // Create and initialize a boolean array
    bool primeNumber[n + 1];
    memset(primeNumber, true, sizeof(primeNumber));
    for (int j = 2; j * j <= n; j++) {
        if (primeNumber[j] == true) {
            // Update all multiples of i as false
            for (int k = j * j; k <= n; k += j)
                primeNumber[k] = false;
        }
    } 
    for (int i = 2; i <= n; i++)
        if (primeNumber[i])
            cout << i << " ";
}
int main()
{
    int n = 25;
    Sieve_Of_Eratosthenes(n);
    return 0;
}

输出

2 3 5 7 11 13 17 19 23

埃拉托斯特尼筛法 Python 程序示例

def SieveOfEratosthenes(n):
# Create a boolean array
	primeNumber = [True for i in range(n+2)]
	i = 2
	while (i * i <= n):
		if (primeNumber[i] == True):
			# Update all multiples of i as false
			for j in range(i * i, n+1, i):
				primeNumber[j] = False
		i += 1
	for i in range(2, n):
		if primeNumber[i]:
			print(i)
n = 25
SieveOfEratosthenes(n)

输出

分段筛法

我们已经看到，埃拉托斯特尼筛法需要遍历整个数字范围。因此，它需要 O(n) 的内存空间来存储数字。当尝试查找大范围内的素数时，情况会变得复杂。分配如此大的内存空间对于更大的 n 是不可行的。

通过引入一些新功能可以优化该算法。其思想是将数字范围分成更小的段，然后逐个计算这些段中的素数。这是降低空间复杂度的一种有效方法。这种方法称为分段筛法。

优化可以通过以下方式实现：

使用简单的筛法查找从 2 到的素数并将它们存储在数组中。
将范围 [0…n-1] 分成大小最多为的多个段。
对于每个段，遍历该段并标记步骤 1 中找到的素数的倍数。此步骤最多需要 O()。常规筛法需要 O(n) 的辅助内存空间，而分段筛法需要

O() 的辅助空间，对于大的 n 来说这是一个很大的改进。该方法也有缺点，因为它不会提高时间复杂度。

复杂度分析

空间复杂度

简单的埃拉托斯特尼筛法算法需要 O(n) 的内存空间。而分段筛法需要
O() 的辅助空间。

时间复杂度

常规埃拉托斯特尼筛法算法的时间复杂度为 O(n*log(log(n)))。下面将讨论此复杂度的原因。

对于给定的数字 n，标记一个合数（即非素数）所需的时间是恒定的。因此，循环运行的次数等于：

n/2 + n/3 + n/5 + n/7 + ……∞

= n * (1/2 + 1/3 + 1/5 + 1/7 +…….∞)

素数和的调和级数可以推断为 log(log(n))。

(1/2 + 1/3 + 1/5 + 1/7 +…….∞) = log(log(n))

因此，时间复杂度将是：

T(n) = n * (1/2 + 1/3 + 1/5 + 1/7 + ……∞)

= n * log(log(n))

因此时间复杂度为 O(n * log(log(n)))

接下来，您将学习帕斯卡三角形

摘要

埃拉托斯特尼筛法在给定的上限内过滤素数。
素数的过滤从最小的素数“2”开始。这是通过迭代完成的。
迭代次数一直到 n 的平方根，其中 n 是给定的数字范围。
经过这些迭代后，剩下的数字就是素数。

算法 埃拉托斯特尼筛法

相关文章

伪代码

埃拉托斯特尼筛法 C/C++ 代码示例

埃拉托斯特尼筛法 Python 程序示例

分段筛法

复杂度分析

摘要

订阅新闻通讯

算法埃拉托斯特尼筛法