帕斯卡三角形——公式、模式和示例
什么是帕斯卡三角形?
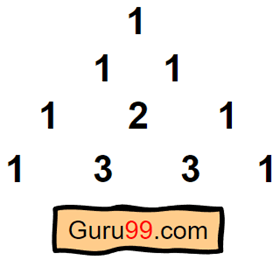
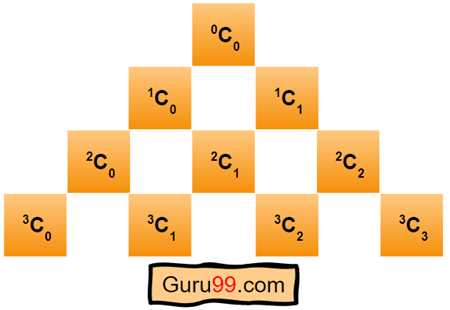
帕斯卡三角形是一个遵循特定模式并与前一行有联系的数字三角形数组。它由布莱兹·帕斯卡发明。这个三角形的第一行只有一个元素。之后,每一行的开头和结尾都是“1”。
帕斯卡三角形的历史
中文书籍《数学艺术九章》包含最早的帕斯卡三角形的例子之一。此外,它包含一些与当今三角形相同的模式和特性。
帕斯卡是欧洲研究该三角形的几个人之一。在此之前,其他数学家也研究过类似的数字三角形数组。
帕斯卡三角形的构造
构建帕斯卡三角形很简单。您需要记住的唯一一件事是,行以 1 开头和结尾。其余数字的规则如下
对于任意行 r 和列 c,该数字将是行 r-1 的列 c-1 和列 c 的总和。
此处,
- r = 3,4,5….
- n 和 c = 2,3,4,…r-1。
以下是构建帕斯卡三角形的步骤
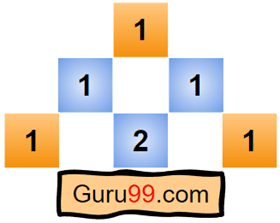
第一步) 让我们从填充两行开始。
第二步) 第三行的第二个元素是第二行第一个数字和第二个数字的总和。
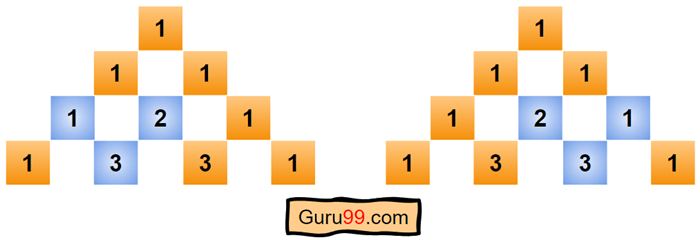
第三步) 第四行将以“1.”开头。第二个数字是 3,它是 1 和 2(蓝色高亮部分)的总和。
下图显示了如何填充第四行
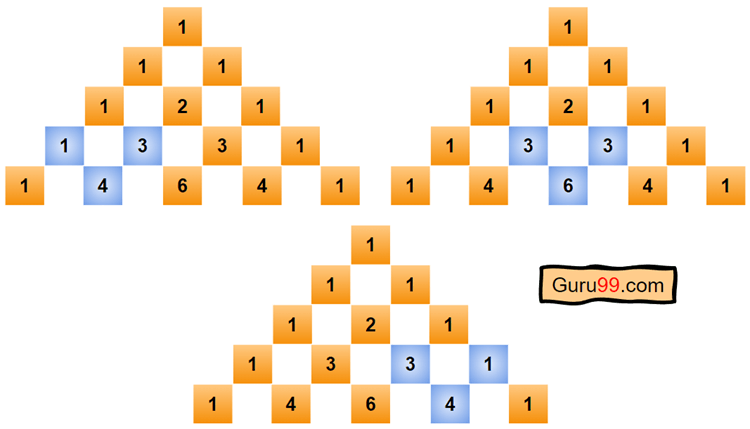
第四步) 第五行将包含五个数字。我们已经从前面的步骤中知道了填充行的模式。
帕斯卡三角形公式 – 二项式系数
二项式系数是表示从 n 个元素的集合中选择 k 个元素的各种方法的数字。通常,它写成“C(n,k)”或“n choose k”。
二项式系数定义为
“!” 表示“阶乘”。
n! = n.(n-1). (n-2)…3.2.1
例如,
5! = 5.4.3.2.1
= 120
所以,假设 C(5,3) 或 5 choose 3 = 5! / 3!(5-3)!
= 120/(12)
= 10
方法一:通过前一行构建帕斯卡三角形
此过程中的步骤与帕斯卡三角形中的步骤相同。假设我们想创建多达七行的帕斯卡三角形。
完成此操作的步骤如下
第一步) 最顶行的开头是“1”。
第二步) 对于行“r”,“c”项将是“r-1”行数字的“c-1”和“c”的乘积。
第三步) 行中的第一个和最后一个数字始终是“1”。
我们必须遵循这三个简单的步骤来创建帕斯卡三角形。
通过前一行构建帕斯卡三角形的 C++ 代码
#include <bits/stdc++.h>
using namespace std;
void printRow(int n)
{
int numbers[n][n];
for (int row = 0; row < n; row++)
{
for (int col = 0; col <= row; col++)
{
if (col == 0 || col == row)
{
numbers[row][col] = 1;
}
else
{
numbers[row][col] = numbers[row - 1][col - 1] + numbers[row - 1][col];
}
cout << numbers[row][col] << "\t";
}
cout << endl;
}
}
int main()
{
int n;
cout << "How many rows: ";
cin >> n;
printRow(n);
}
输出
How many rows: 7 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1
通过前一行构建帕斯卡三角形的 Python 代码
def printRow(n):
numbers = [[0 for row in range(n)]
for col in range(n)
]
for row in range(len(numbers)):
for col in range(0, row+1):
if row == col or col == 0:
numbers[row][col] = 1
else:
numbers[row][col] = numbers[row-1][col-1]+numbers[row-1][col]
print(numbers[row][col],end="\t")
print("\n")
n = int(input("How many rows: "))
printRow(n)
帕斯卡三角形示例输出
How many rows: 7 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1
复杂度分析
实现中使用了二维数组。鉴于 N 是帕斯卡三角形的行数。这需要 N^2 个单元空间。因此,O 是空间复杂度 (N^2)**。**
函数中有两个循环,每个循环运行“N”次。因此,时间复杂度也是 **O(N^2)** 或平方时间复杂度。
方法二:通过计算二项式系数构建帕斯卡三角形
我们可以使用二项式系数轻松地推导出帕斯卡三角形的数字。这是图
以下是通过计算二项式构建帕斯卡三角形的步骤
第一步) 最顶行的第一个是 C(0,0)。使用上面的二项式系数公式,C(0,0) = 1。因为 0! = 1。
第二步) 对于行“i”,将总共有“i”个元素。每个元素将通过 C(n,r) 计算,其中 n 为 i-1。
第三步) 重复步骤 2,直到达到所需的帕斯卡三角形行数。
通过二项式系数计算帕斯卡三角形的 C++ 代码
#include <iostream>
using namespace std;
int factorial(int n)
{
int result = 1;
for (int i = 1; i <= n; i++)
{
result *= i;
}
return result;
}
int binomialCoefficient(int n, int r)
{
int result = 1;
if (r > n)
{
return -1;
}
result = factorial(n) / (factorial(r) * factorial(n - r));
return result;
}
void printPascalTriangle(int row)
{
for (int i = 0; i <= row; i++)
{
for (int j = 0; j <= i; j++)
{
cout << binomialCoefficient(i, j) << "\t";
}
cout << endl;
}
}
int main()
{
int n;
cout << "Enter row number: ";
cin >> n;
printPascalTriangle(n);
}
输出
Enter row number: 9 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1
通过二项式系数计算帕斯卡三角形的 Python 代码
def factorial(n):
result = 1
for i in range(1,n+1):
result*=i
return result
def binomialCoefficient(n,r):
result =1
if r>n:
return None
result = factorial(n) / (factorial(r) * factorial(n - r))
return int(result)
def printPascalTriangle(row):
for i in range(row+1):
for j in range(i+1):
print(binomialCoefficient(i, j), end="\t")
print()
# print(binomialCoefficient(3, 2))
n = int(input("Enter row number: "))
printPascalTriangle(n)
帕斯卡三角形示例输出
Enter row number: 8 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1
复杂度分析
实现中使用了三个循环。一个循环用于计算二项式系数,另外两个循环用于创建所有行的数字。关于行数,我们有三个循环执行“n”次。因此,总时间复杂度为 0(n^3)**。**
由于我们没有将任何数据存储在存储器中,因此空间复杂度现在是常数。程序计算元素,并在行中打印。因此,空间复杂度降至 0(1)。
方法三:通过修改后的二项式系数构建帕斯卡三角形
在前一种技术中,我们已经看到了如何使用二项式系数计算帕斯卡三角形的每个元素。此方法将从 C.(n, r-1) 确定 C(n,r)。它将简化一阶。
以下是构建帕斯卡三角形的方法(修改二项式系数)
第一步) 用“1”初始化第一行
第二步) 计算 C(n,r),其中“n”是行号,“r”是列或元素。将值赋给变量 C。
第三步) 对于计算 C(n,k),它将是 C*(n-k)/k。现在,将此值赋给 C。
第四步) 继续步骤 3,直到“k”到达行的末尾。每次迭代后,将 K 的值加一。
通过修改二项式系数计算帕斯卡三角形的 C++ 代码
#include <bits/stdc++.h>
using namespace std;
void printpascalTriangle(int n)
{
for (int row = 1; row <= n; row++)
{
int previous_coef = 1;
for (int col = 1; col <= row; col++)
{
cout << previous_coef << "\t";
previous_coef = previous_coef * (row - col) / col;
}
cout << endl;
}
}
int main()
{
int n;
cout << "How many rows: ";
cin >> n;
printpascalTriangle(n);
}
输出
How many rows: 5 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1
通过修改二项式系数计算帕斯卡三角形的 Python 代码
def printpascalTriangle(n):
for row in range(1, n+1):
previous_coef = 1
for col in range(1, row+1):
print(previous_coef, end="\t")
previous_coef = int(previous_coef*(row-col)/col)
print()
n = int(input("How many rows: "))
printpascalTriangle(n)
帕斯卡三角形模式输出
How many rows: 5 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1
复杂度分析
实现中有两个循环。每个循环最多运行“n”次,其中“n”表示帕斯卡三角形的行数。因此,时间复杂度为 **O(n^2)**,平方时间。
在空间复杂度方面,我们不需要任何数组来存储。我们只使用了一个变量来存储前一个二项式系数。因此,我们只需要一个额外的空间。空间复杂度变为 **O(1)**。
帕斯卡三角形的应用
以下是帕斯卡三角形的一些应用
二项式展开:我们可以从帕斯卡三角形确定二项式展开的系数。这是一个例子
| (x+y)0 | 1 |
| (x+y)1 | 1.x + 1.y |
| (x+y)2 | 1x2 + 2xy + 1y2 |
| (x+y)3 | 1x3 + 3x2y + 3xy2 + 1y3 |
| (x+y)4 | 1x4 + 4x3y + 6x2y2 + 4xy3 + 1y4 |
计算组合:我们已经看到帕斯卡三角形的元素相当于二项式系数。例如,如果你有 6 个球,并且被要求选择 3 个球,那将是 **6C3。** 或者,你可以在帕斯卡三角形的第 6 行的第 3 个元素中找到数字。
关于帕斯卡三角形的有趣事实
以下是关于帕斯卡三角形的一些有趣事实
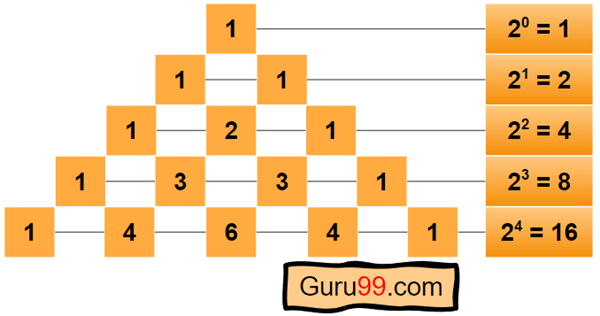
- 一行中所有元素的总和总是 2 的幂。
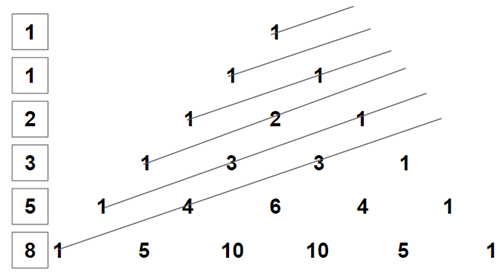
- 对行元素进行对角线求和会生成斐波那契数列。
摘要
- 帕斯卡三角形给出了二项式展开的系数。
- 帕斯卡三角形的每一行都以“1”开头和结尾。中间值是前一行两个元素的总和。
- 对帕斯卡三角形中所有元素进行对角线加法将得到 斐波那契数列。
- 帕斯卡三角形也可以用二项式系数生成。