广度优先搜索（BFS）算法及示例

什么是BFS算法（广度优先搜索）？

广度优先搜索（BFS）是一种用于图数据或搜索树或遍历结构的算法。BFS的全称是广度优先搜索。

该算法以准确的广度优先方式高效地访问和标记图中的所有关键节点。该算法选择图中的一个节点（初始节点或源点），然后访问与所选节点相邻的所有节点。请记住，BFS一次访问一个节点。

一旦算法访问并标记了起始节点，它就会移动到最近的未访问节点并进行分析。访问后，所有节点都会被标记。这些迭代将继续，直到图的所有节点都已成功访问并标记。

什么是图遍历？

图遍历是用于定位图中顶点位置的常用方法。它是一种高级搜索算法，可以快速准确地分析图，并标记已访问顶点的顺序。此过程使您能够快速访问图中的每个节点，而不会陷入无限循环。

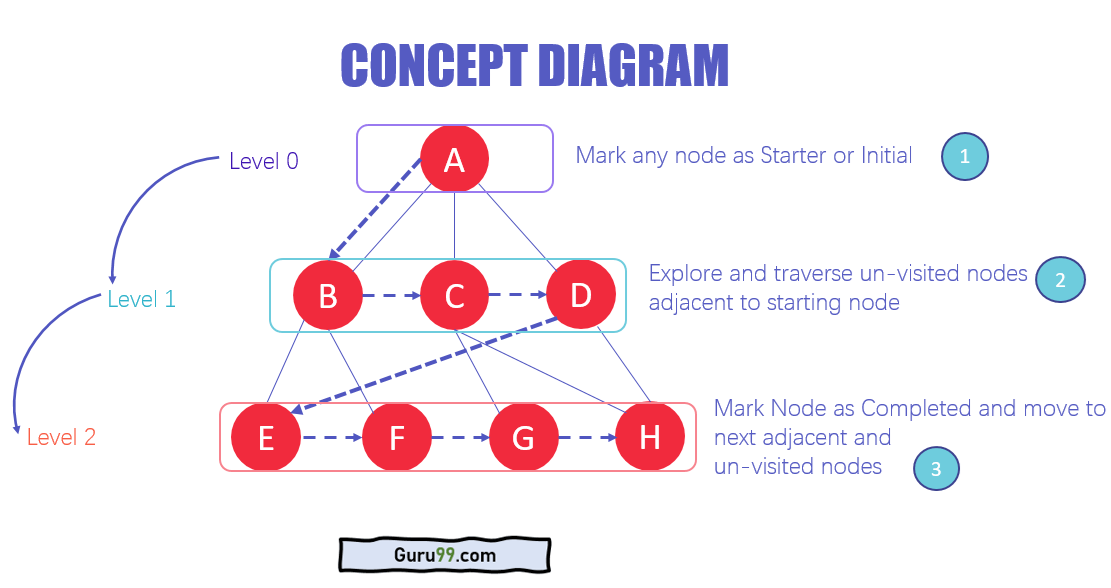
BFS算法的架构

在数据的各个层级中，您可以将任何节点标记为开始或初始节点以开始遍历。BFS将访问该节点并将其标记为已访问，然后将其放入队列。
现在BFS将访问最近的未访问节点并对其进行标记。这些值也会被添加到队列中。队列遵循FIFO模型。
以类似的方式，图上剩余的最近的未访问节点被分析、标记并添加到队列中。这些项目在接收时会从队列中删除并作为结果打印出来。

为什么我们需要BFS算法？

使用BFS算法搜索数据集有许多原因。使该算法成为首选的一些最重要方面是：

BFS可用于分析图中的节点并构建通过这些节点的遍历最短路径。
BFS可以在最少的迭代次数中遍历图。
BFS算法的架构简单而强大。
与其他算法相比，BFS算法的结果具有高度的准确性。
BFS迭代是无缝的，该算法没有陷入无限循环问题的可能性。

BFS算法是如何工作的？

图遍历要求算法访问、检查和/或更新树状结构中每个未访问的节点。图遍历按访问图中节点的顺序进行分类。

BFS算法从图中的第一个或起始节点开始操作，并对其进行彻底遍历。成功遍历初始节点后，将访问并标记图中的下一个未遍历顶点。

因此，可以说当前顶点的所有相邻节点都在第一次迭代中被访问和遍历。简单的队列方法用于实现BFS算法的工作，它包括以下步骤：

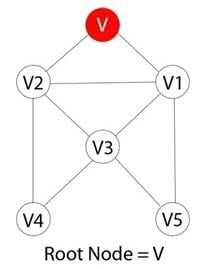
步骤 1)

图中的每个顶点或节点都是已知的。例如，您可以将节点标记为V。

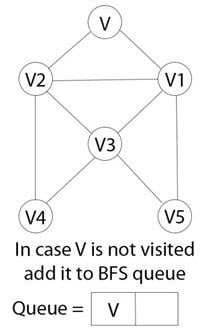
步骤 2)

如果未访问顶点V，则将顶点V添加到BFS队列中。

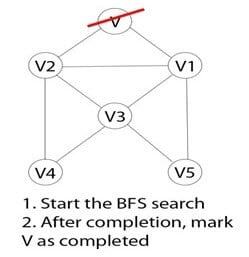
步骤 3)

开始BFS搜索，完成后将顶点V标记为已访问。

步骤 4)

BFS队列仍不为空，因此从队列中删除图的顶点V。

步骤 5)

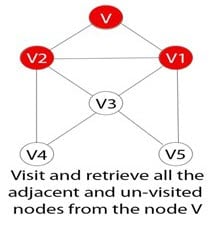
检索图中与顶点V相邻的所有剩余顶点。

步骤 6)

对于每个相邻的顶点（例如V1），如果尚未访问，则将V1添加到BFS队列中。

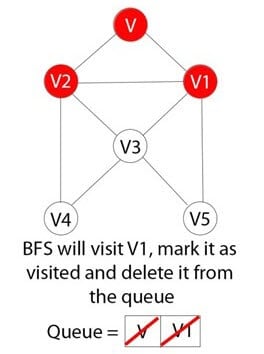
步骤7）

BFS将访问V1并将其标记为已访问，然后从队列中删除。

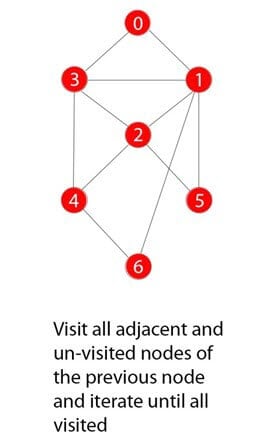
BFS算法示例

步骤 1)

您有一个包含0到6七个数字的图。

步骤 2)

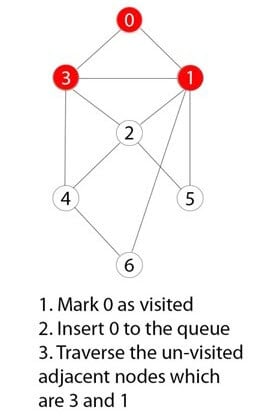
0被标记为根节点。

步骤 3)

0被访问、标记并插入队列数据结构。

步骤 4)

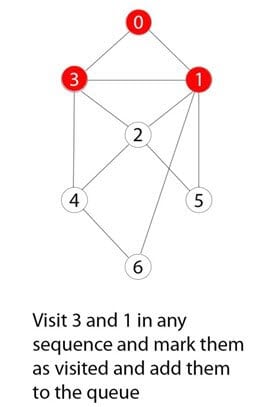
0的相邻且未访问的节点被访问、标记并插入队列。

步骤 5)

遍历迭代会重复进行，直到所有节点都被访问。

BFS算法规则

以下是使用BFS算法的重要规则：

BFS使用队列（FIFO-先进先出）数据结构。
将图中的任何节点标记为根节点，并从该节点开始遍历数据。
BFS遍历图中的所有节点，并逐个删除已完成的节点。
BFS访问相邻的未访问节点，将其标记为已完成，并将其插入队列。
如果找不到相邻的顶点，则从队列中删除前一个顶点。
BFS算法会一直迭代，直到图中的所有顶点都被成功遍历并标记为已完成。
BFS在从任何节点遍历数据时不会产生任何循环。

BFS算法的应用

让我们看看BFS算法实现可能非常有效的几个实际应用。

无权图：BFS算法可以轻松创建最短路径和最小生成树，以最短的时间最高精度访问图的所有顶点。
P2P网络：BFS可用于定位点对点网络中所有最近或相邻的节点。这将更快地找到所需数据。
网络爬虫：搜索引擎或网络爬虫可以通过采用BFS轻松构建多个级别的索引。BFS实现从源（网页）开始，然后访问该源的所有链接。
导航系统：BFS可以帮助查找主位置或源位置的所有相邻位置。
网络广播：BFS算法指导广播的数据包，以查找并到达它所寻址的所有节点。

摘要

图遍历是一个独特的过程，它要求算法访问、检查和/或更新树状结构中每个未访问的节点。BFS算法也基于类似原理工作。
该算法可用于分析图中的节点，并构建通过这些节点的遍历最短路径。
该算法在最少的迭代次数和最短的时间内遍历图。
BFS选择图中的一个节点（初始节点或源点），然后访问与所选节点相邻的所有节点。BFS一次访问一个节点。
BFS将已访问和标记的数据放入队列。队列遵循先进先出原则。因此，先放入图中的元素先被删除并作为结果打印出来。
BFS算法永远不会陷入无限循环。
由于其高精度和强大的实现，BFS被用于许多现实生活中的解决方案，例如P2P网络、网络爬虫和网络广播。