二叉搜索树（BST）与示例

什么是二叉搜索树？

二叉搜索树是一种用于分析节点、其左右分支的先进算法，这些节点以树状结构建模并返回其值。BST 基于基本二叉搜索算法的架构；因此，它能够更快地查找、插入和删除节点。这使得程序非常快速且准确。

二叉搜索树的属性

BST 由多个节点组成，具有以下属性

树的节点以父子关系表示
每个父节点可以有零个子节点，或者最多在左右两侧有两个子节点或子树。
每个子树，也称为二叉搜索树，在其自身左右两侧都有子分支。
所有节点都通过键值对链接。
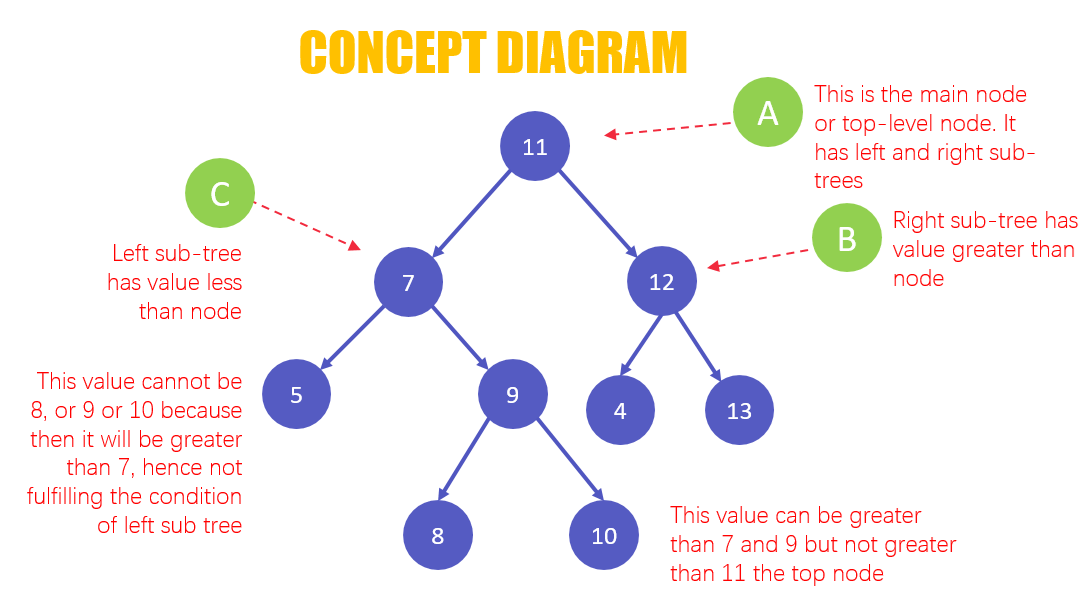
位于左子树的节点的键小于其父节点的键
同样，左子树节点的键值小于其父节点的键。

有一个主节点或父节点级别 11。在其下方，有左右节点/分支，它们有自己的键值。
右子树的键值大于父节点
左子树的值小于父节点

为什么我们需要二叉搜索树？

使二叉搜索树成为任何现实世界问题的最佳解决方案的两个主要因素是速度和准确性。
由于二叉搜索以类似分支的格式存在父子关系，因此算法知道需要在树的哪个位置搜索元素。这减少了程序为了找到所需元素而必须进行的键值比较次数。
此外，如果待搜索的元素大于或小于父节点，节点就知道应该搜索树的哪一侧。原因是，左子树总是小于父节点，而右子树的值总是等于或大于父节点。
BST 通常用于实现复杂的搜索、强大的游戏逻辑、自动完成活动和图形。
该算法有效地支持搜索、插入和删除等操作。

二叉树的类型

三种二叉树是

完全二叉树：树中的所有层都已满，除了最后一层可能不完整。同样，所有节点都已填满，向左侧倾斜。
满二叉树：除叶子节点外，所有节点都有 2 个子节点。
平衡二叉树或完美二叉树：在树中，所有节点都有两个子节点。此外，每个子节点都处于同一级别。

如果您对数据结构中的二叉树感兴趣，请了解更多信息。

二叉搜索树如何工作？

树总是有一个根节点和进一步的子节点，无论是在左侧还是右侧。算法通过将值与根节点及其在左侧或右侧子树中的子节点进行比较来执行所有操作。

根据要插入、搜索或删除的元素，在比较之后，算法可以轻松地丢弃根节点的左子树或右子树。

BST 主要提供以下三种操作供您使用

搜索：在二叉树中搜索元素
插入：将元素添加到二叉树
删除：从二叉树中删除元素

每个操作都有其自身的结构和执行/分析方法，但其中最复杂的是删除操作。

搜索操作

始终从根节点开始分析树，然后根据要定位的元素大于或小于根节点，进一步移至根节点的右子树或左子树。

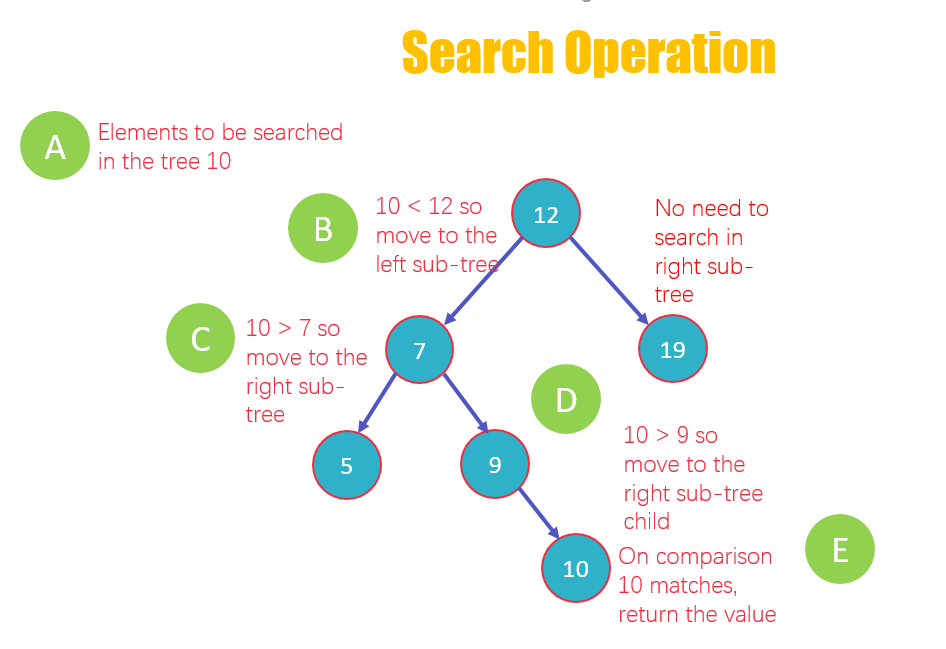
要搜索的元素是 10
将元素与根节点 12 进行比较，10 < 12，因此移至左子树。无需分析右子树
现在将 10 与节点 7 进行比较，10 > 7，因此移至右子树
然后将 10 与下一个节点 9 进行比较，10 > 9，在右子树的子节点中查找
10 与节点中的值匹配，10 = 10，将值返回给用户。

BST 搜索的伪代码

search(element, root)
     if !root
    	return -1
     if root.value == element
    	return 1
     if root.value < element
    	search(element, root.right)
      else
    	search(element, root.left)

插入操作

这是一个非常直接的操作。首先，插入根节点，然后将下一个值与根节点进行比较。如果值大于根节点，则将其添加到右子树；如果值小于根节点，则将其添加到左子树。

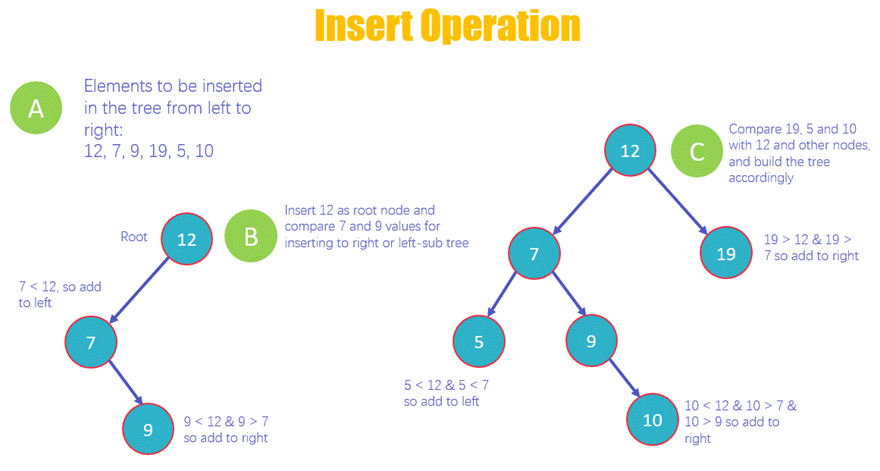
这里有一个包含 6 个元素的列表，需要按从左到右的顺序插入 BST 中
将 12 插入为根节点，并比较下一个值 7 和 9，以便相应地插入到右子树和左子树中
将剩余的值 19、5 和 10 与根节点 12 进行比较并将它们放置好。19 > 12，将其作为 12 的右子节点；5 < 12 且 5 < 7，因此将其作为 7 的左子节点。现在比较 10，10 < 12 且 10 > 7 且 10 > 9，将 10 作为 9 的右子树。

BST 插入节点的伪代码

insert (element, root)
    Node x = root
    Node y = NULL
    while x:
    	y = x
    if x.value < element.value
        x = x.right
    else
        x = x.left
    if y.value < element
    	y.right = element
    else
    	y.left = element

删除操作

为了从 BST 中删除节点，存在一些情况，例如删除根节点或删除叶子节点。此外，在删除根节点后，我们需要考虑根节点。

假设我们要删除一个叶子节点，我们可以直接删除它，但如果我们想删除一个根节点，我们需要用另一个节点替换根节点的值。让我们看下面的例子

情况 1- 零个子节点的节点：这是最简单的情况，您只需删除没有右侧或左侧子节点的节点。
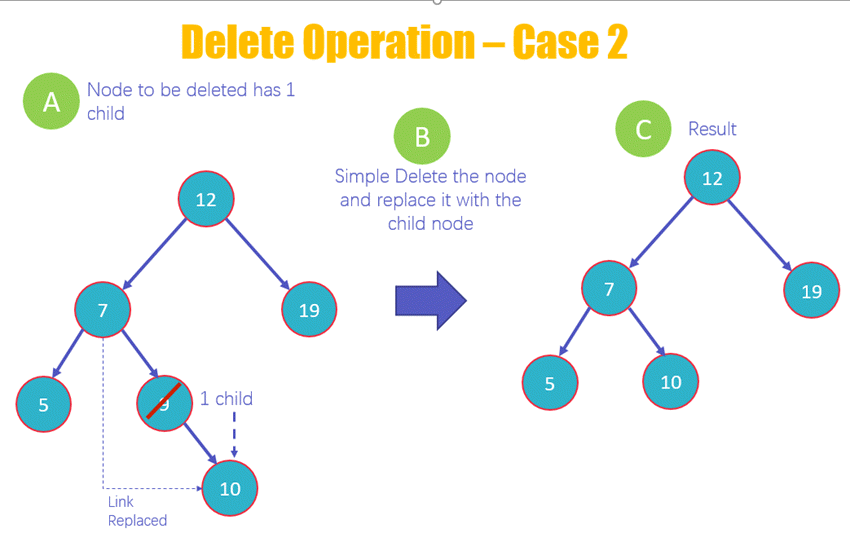
情况 2 – 只有一个子节点的节点：删除节点后，只需将其子节点与被删除值的父节点连接起来。
情况 3 两个子节点的节点：这是最困难的情况，它遵循以下两个规则
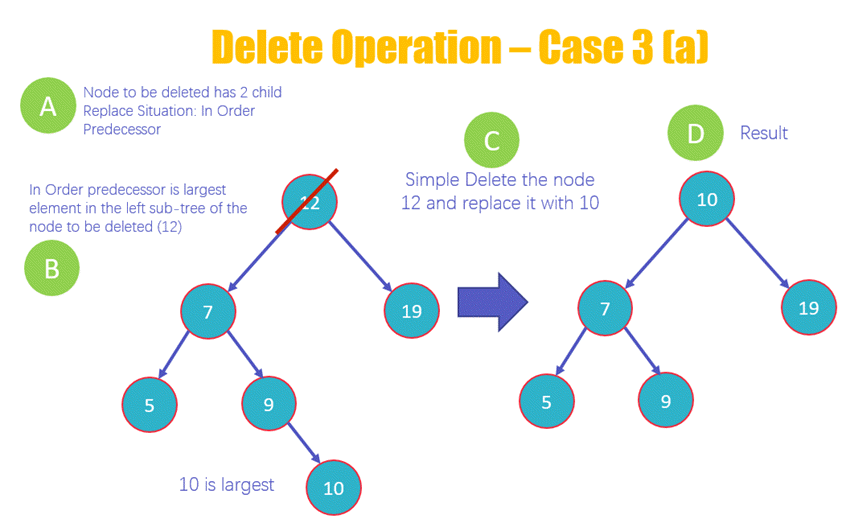
3a – 中序前驱：您需要删除带有两个子节点的节点，并用被删除节点左子树中的最大值替换它
3b – 中序后继：您需要删除带有两个子节点的节点，并用被删除节点右子树中的最大值替换它

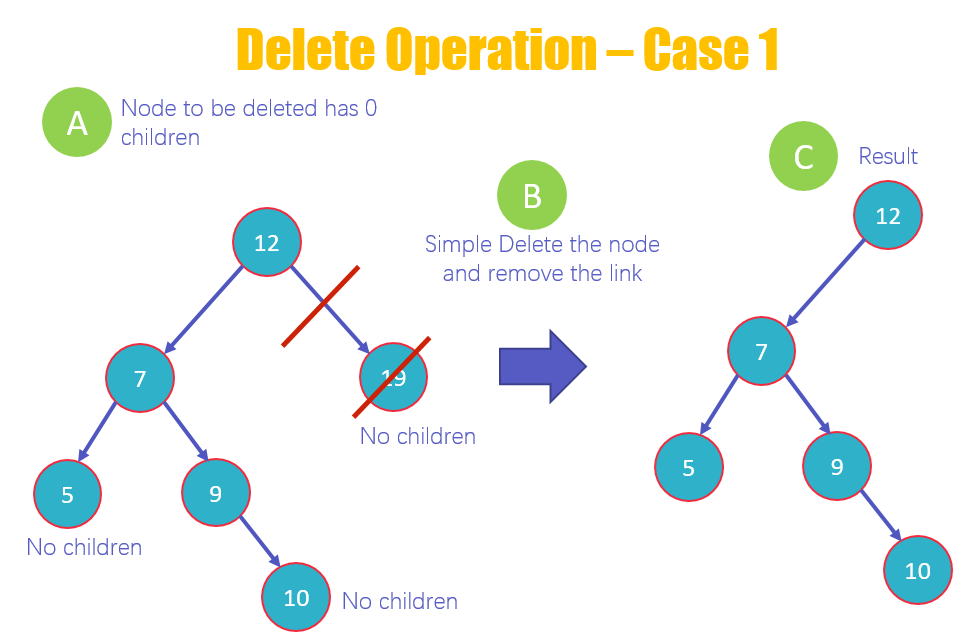
这是删除的第一种情况，您删除的是一个没有子节点的节点。正如您在图中看到的，19、10 和 5 没有子节点。但我们将删除 19。
删除值 19 并从节点中移除链接。
查看不包含 19 的 BST 的新结构

这是删除的第二种情况，您删除的是只有一个子节点的节点，正如您在图中看到的，9 有一个子节点。
删除节点 9 并用其子节点 10 替换它，并将从 7 到 10 的链接添加上去
查看不包含 9 的 BST 的新结构

在这里，您将删除带有两个子节点的节点 12
节点删除将根据中序前驱规则进行，这意味着 12 左子树中的最大值将替换它。
删除节点 12 并用 10 替换它，因为它是左子树中的最大值
查看删除 12 后 BST 的新结构

1 删除带有两个子节点的节点 12
2 节点删除将根据中序后继规则进行，这意味着 12 右子树中的最大值将替换它
3 删除节点 12 并用 19 替换它，因为它是右子树中的最大值
4 查看删除 12 后 BST 的新结构

删除节点的伪代码

delete (value, root):
    Node x = root
    Node y = NULL
# searching the node
    while x:
    	y = x
    if x.value < value
        x = x.right
    else if x.value > value
        x = x.left
    else if value == x
        break
# if the node is not null, then replace it with successor
    if y.left or y.right:
    	newNode = GetInOrderSuccessor(y)
    	root.value = newNode.value
# After copying the value of successor to the root #we're deleting the successor
    	free(newNode)
    else
    	free(y)

重要术语

插入：在树中插入元素/创建树。
搜索：在树中搜索元素。
前序遍历：以前序方式遍历树。
中序遍历：以中序方式遍历树。
后序遍历：以后序方式遍历树。

摘要

BST 是一种高级算法，它根据节点值与根节点的比较来执行各种操作。
父子层级中的任何一个点都代表节点。始终至少存在一个父节点或根节点。
有一个左子树和右子树。左子树包含小于根节点的值。但是，右子树包含大于根节点的值。
每个节点可以有零个、一个或两个子节点。
二叉搜索树支持搜索、插入和删除等基本操作。
删除是最复杂的，有多种情况，例如，没有子节点的节点、有一个子节点的节点以及有两个子节点的节点。
该算法用于游戏、自动完成数据和图形等现实解决方案。