二分查找算法(带示例)
在学习二分查找之前,我们先来学习
什么是搜索?
搜索是一种实用工具,使用户能够查找存储在数据库中的文档、文件、媒体或任何其他类型的数据。搜索基于匹配标准和将其显示给用户的简单原则。这样,最基本的搜索功能就可以工作了。
什么是二分查找?
二分查找是一种高级的搜索算法,它从已排序的项目列表中查找并获取数据。其核心工作原理是不断将列表中的数据分成两半,直到找到所需的值并显示给用户。二分查找通常被称为半区间查找或对数查找。
二分查找如何工作?
二分查找的工作方式如下:
- 搜索过程开始于定位已排序数据数组的中间元素。
- 之后,将键值与该元素进行比较。
- 如果键值小于中间元素,则搜索会分析中间元素以上的数值进行比较和匹配。
- 如果键值大于中间元素,则搜索会分析中间元素以下的数值进行比较和匹配。
二分查找示例
我们来看字典的例子。如果您需要查找某个单词,没有人会按顺序逐个单词地查找,而是会随机定位最近的单词来搜索所需的单词。
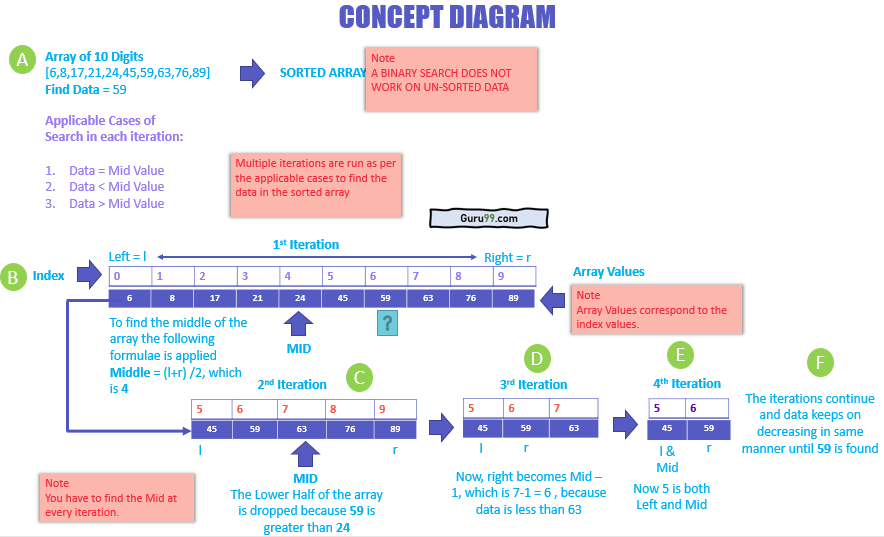
上图说明了以下内容:
- 您有一个包含 10 个数字的数组,需要找到元素 59。
- 所有元素都标有索引 0-9。现在,计算数组的中间值。为此,您取索引的左边界和右边界值,然后除以 2。结果是 4.5,但我们取其整数部分。因此,中间值是 4。
- 由于 59 大于 24,算法会丢弃中间值 (4) 到最低边界的所有元素,现在数组中只剩下 5 个元素。
- 现在,59 大于 45 但小于 63。中间值是 7。因此,右索引值变为中间值 - 1,即 6,而左索引值与之前一样,即 5。
- 此时,您知道 59 在 45 之后。因此,左索引 5 也成为中间值。
- 这些迭代会一直持续,直到数组缩小到只剩一个元素,或者要查找的项成为数组的中间元素。
示例 2
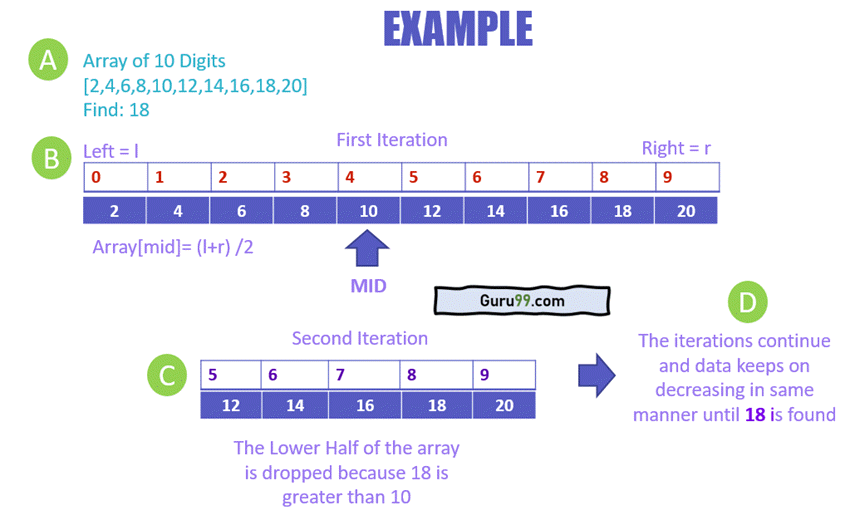
让我们看下面的例子来理解二分查找的工作原理。
- 您有一个从 2 到 20 的已排序值数组,需要找到 18。
- 下限和上限的平均值为 (l + r) / 2 = 4。要搜索的值大于中间值 4。
- 小于中间值的数组值将被从搜索中排除,而大于中间值 4 的值将被搜索。
- 这是一个递归划分过程,直到找到要搜索的实际项。
为什么我们需要二分查找?
以下原因是二分查找成为搜索算法的更好选择:
- 二分查找在已排序的数据上都能高效工作,无论数据大小如何。
- 二分算法不是按顺序遍历数据进行搜索,而是随机访问数据来查找所需元素。这使得搜索周期更短、更准确。
- 二分查找基于排序原理对已排序数据进行比较,而不是使用通常较慢且不准确的相等比较。
- 在每次搜索周期后,算法都会将数组大小分成两半,因此在下一次迭代中,它只会在剩余的一半数组中工作。
学习我们的下一个教程:线性搜索:Python、C++ 示例
摘要
- 搜索是一种实用工具,使用户能够搜索文档、文件和其他类型的数据。二分查找是一种高级的搜索算法,它从已排序的项目列表中查找并获取数据。
- 二分查找通常被称为半区间查找或对数查找。
- 它通过在每次迭代中将数组分成两半来工作,直到找到所需的元素。
- 该二分算法通过将左右边界索引值的总和除以 2 来获取数组的中间值。然后,根据要查找的元素,算法会从数组中间删除较低或较高的边界元素。
- 该算法随机访问数据以查找所需元素。这使得搜索周期更短、更准确。
- 二分查找基于排序原理对已排序数据进行比较,而不是使用通常较慢且不准确的相等比较。
- 二分查找不适用于未排序的数据。