线性搜索：Python、C++ 示例

什么是搜索算法？

搜索算法旨在从具有给定数据结构的元素集合中查找元素或对象。例如，从给定的身高列表中搜索最小身高，或从数字列表或数组中搜索最高分数。一些流行的搜索算法包括“线性搜索”、“二分搜索”、“跳转搜索”、“斐波那契搜索”等。

什么是线性搜索？

线性搜索是最简单的搜索算法之一。它逐个遍历给定列表或数组，搜索给定元素。线性搜索会遍历整个列表，并检查是否有任何特定元素等于搜索元素。它也被称为 **顺序搜索**。

线性搜索函数做什么？

给定一个整数数组“Numbers”，一个变量“item”包含要搜索的整数。

现在，线性搜索算法可以提供以下输出：

“-1”；表示在数组中未找到给定元素
0 到 n-1 之间的任何数字；表示找到了搜索元素，并返回数组中该元素的索引。这里，“n”代表数组的大小。

线性搜索是如何工作的？

假设有一个包含整数的数组。任务是在数组中找到给定的数字。

如果数字位于数组中，我们需要返回该数字的索引。
如果未找到给定数字，则返回-1。

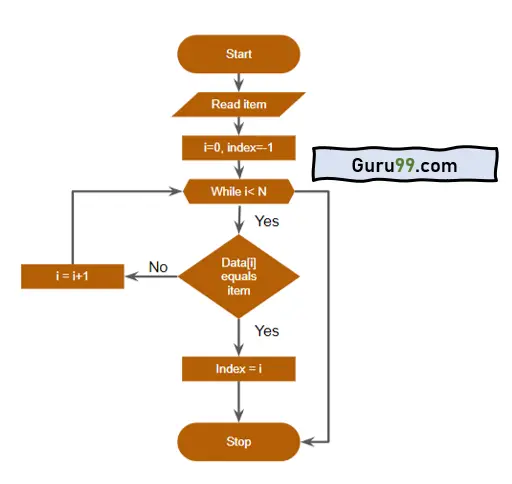
在流程图中，“Data”是整数数组，“N”是数组的大小，“item”是我们要在数组中搜索的数字。

线性搜索算法流程图

流程图步骤如下：

步骤 1) 读取搜索项“item”。

步骤 2) 初始化 i=0 和 index=-1

步骤 3) 如果 i<N，转到步骤 4。否则，转到步骤 8。

步骤 4) 如果 Data[i] 等于“item”，则转到步骤 5。否则，转到步骤 6。

步骤 5) Index = i（因为在索引 i 处找到了该项）。转到步骤 8。

步骤 6) i = i +1。

步骤 7) 转到步骤 3。

步骤 8) 停止。

为简单起见，我们提供了一个整数数组的示例。线性搜索也适用于字符串、对象数组或结构。

顺序搜索算法的伪代码

function linearSearch: in →Data[], item
foundAt = -1
for i in (0 to data.length): if data[i] equals item
// item is found in the array
// returning the index
return i
// item not found in the array
// -1 means no item found, as negative index is not valid
return -1

C++ 线性搜索代码示例

#include < bits / stdc++.h >
    using namespace std;
int linearSearch(int * arr, int item, int n) {
    int idx = -1;
    for (int i = 0; i < n; i++) {
        if (arr[i] == item) {
            idx = i;
            break;
        }
    }
    return idx;
}
int main() {
    int array[] = {
        1, 9, 8, 7, 6, 3, 11, 4, 6, 9, 7, 2, 0, 19, -10
    };
    int n = sizeof(array) / sizeof(arr[0]);
    int item;
    cout << "Enter a number to search: ";
    cin >> item;
    int idx = linearSearch(arr, item, n);
    if (idx >= 0) {
        cout << item << " is found at index " << idx << endl;
    } else {
        cout << "Could not find " << item << " in the array" << endl;
    }
}

输出

Enter a number to search: -10
-10 is found at index 14

Python 线性搜索代码示例

def linearSearch(data, item):
    for i in range(len(data)):
    if data[i] == item:
    return i
return -1
data = [1, 9, 8, 7, 6, 3, 11, 4, 6, 9, 7, 2, 0, 19, -10]
item = int(input("Enter a number to search: "))
idx = linearSearch(data, item)
if idx >= 0:
    print("{} is found at index {}".format(item, idx))
else :
    print("{} was not found".format(item))

输出

Enter a number to search: -10
-10 is found at index 14

线性搜索算法的复杂度分析

通常，时间复杂度是指执行特定任务所需的 CPU 时间量。在線性搜索算法中，任务是从数组元素中查找搜索键。

时间复杂度有三种类型：

最坏情况场景
最佳情况场景
平均情况场景

线性搜索在最坏情况下的时间复杂度

假设我们需要在一个大小为“n”的数组中执行线性搜索。我们可以在索引 0 到 n-1 之间找到搜索项。在最坏情况下，算法将尝试将数组中的所有元素与搜索元素进行匹配。

在这种情况下，最坏情况复杂度将是 O(n)。这里，“O”-大 O 表示法表示复杂度函数。

线性搜索在最佳情况下的时间复杂度

假设我们要搜索一个位于数组第一个位置的元素。在这种情况下，线性搜索算法将不会搜索数组中的所有 n 个元素。因此，复杂度将是 O(1)。这意味着常数时间。

线性搜索在平均情况下的时间复杂度

当一个元素位于数组的中间索引时，可以认为线性搜索的平均情况复杂度为 O(N)，其中 N 表示数组的长度。

线性搜索算法的空间复杂度

线性搜索的空间复杂度始终为 O(N)，因为在线性搜索函数中我们不需要存储或使用任何类型的临时变量。

如何改进线性搜索算法

在程序生命周期中可以多次进行搜索。我们也有可能正在运行线性搜索算法并多次搜索任何特定的键。如果数组是已排序的，我们可以使用“二分搜索算法”。

假设数组包含一万个数字，目标元素位于第 5000 个索引处。那么，算法将尝试比较 5000 个元素。现在，比较是 CPU 密集型任务。为了优化线性搜索算法，我们有两种选择。

换位法
移到开头

换位法

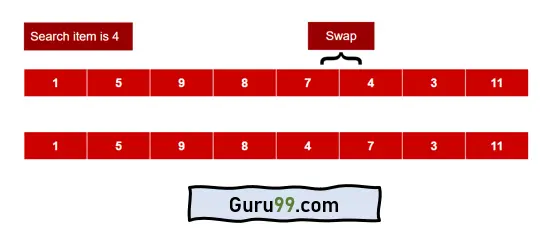
在此方法中，我们将搜索元素与其在数组中的前一个元素进行交换。例如，假设您有一个如下所示的数组

Data[] = {1,5,9,8,7,3,4,11}

现在，我们要搜索 4。换位法的步骤

步骤 1) 在索引 6 处找到“4”。它进行了六次比较。

步骤 2) 交换 data[6] 和 data[5]。然后 data 数组将如下所示

Data[] = {1,5,9,8,7,4,3,11}

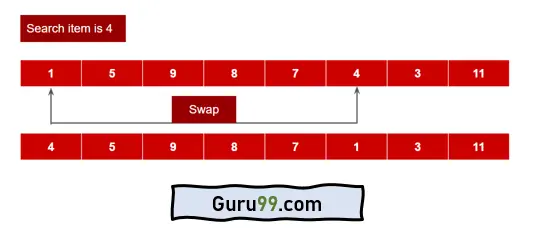
步骤 3) 再次搜索 4。在索引 5 处找到。这次它进行了五次比较。

步骤 4) 交换 data [5] 和 data[4]。然后 data 数组将如下所示

Data [] = {1,5,9,8,4,7,3,11}

现在，如果您注意到，键被搜索的频率越高，其索引就越低。因此，减少了比较次数。

移到开头

在此方法中，我们将搜索元素交换到第 0 个索引。因为如果再次搜索它，我们可以以 O(1) 的时间找到它。

线性搜索算法的应用

以下是我们可以在线性搜索中使用的线性搜索应用程序。

对于小型数组或列表中只有少量元素，使用线性搜索会更方便。
线性搜索方法可用于单维或多维数组或其他数据结构。
通常，线性搜索在“无序”数据中执行搜索非常简单且高效。我们可以轻松地从给定的无序列表中获取单个数据。