数据结构中的二叉树(示例)
什么是二叉树?
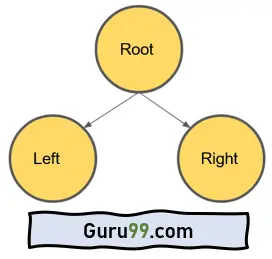
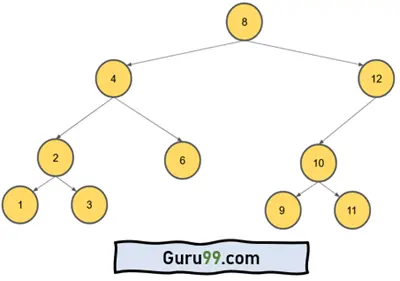
二进制这个词的意思是两个。在树形数据结构“二叉树”中,表示一棵树,其中每个节点最多可以有两个子节点(左节点和右节点)。它是一棵简单的二叉树。
然而,还有另一种更常用的二叉树,具有多种用途。它被称为二叉搜索树(BST)。这种树可以使搜索算法快得多,精确到 log(n) 的时间复杂度。在数据结构中,n 表示二叉树中的节点数。
二叉树和二叉搜索树之间有什么区别?
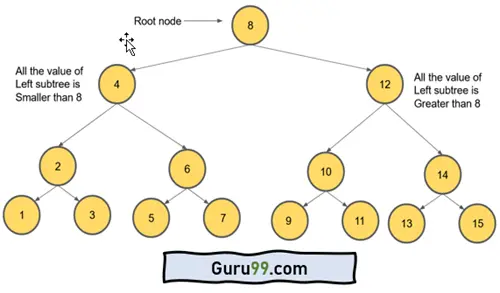
BST 和普通二叉树的区别在于,BST 的左节点值小于根节点,右节点值大于根节点。因此,左子树的值总是小于根节点,右子树的值总是大于根节点。
二叉搜索树示例
下面以二叉搜索树的概念为例。
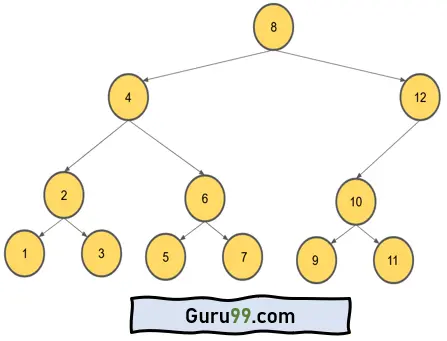
在这里,您可以看到所有节点都遵循给定的规则。二叉搜索树中最大节点数有一个公式。如果我们观察上面的树,我们可以看到除了所有叶节点之外,每个节点都有两个子节点。并且给定二叉树的高度 (h) 为 4。公式是 **2h – 1**。所以,结果是 15。
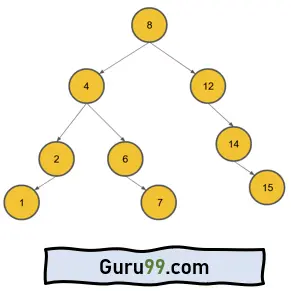
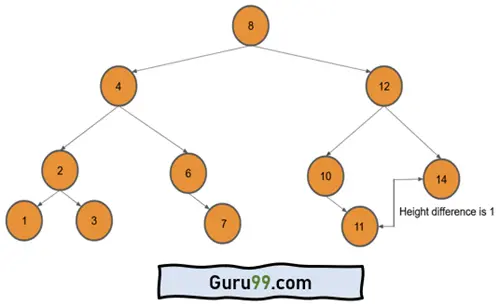
上图不是满二叉树或平衡二叉树,而是称为完全二叉树或平衡二叉树。还有另一种数据结构叫做 AVL(另一种类型的二叉树),它优化了二叉树的高度,并且可以像图 3 一样更快地为 BST 进行搜索。
尝试计算上面给出的二叉树的中序遍历。您会发现它会得到一个非递减的排序数组,并且遍历算法与二叉树相同。
二叉树的类型
这里是一些重要的二叉树类型
- 满二叉树:在此二叉树中,每个节点可以有 0 个或 2 个子节点。此类型的二叉树不允许只有一个子节点。因此,除了叶节点,所有节点都将有 2 个子节点。
- 满二叉树:每个节点可以有 0 个或 2 个节点。这看起来像满二叉树,但所有叶元素都偏向左子树,而满二叉树的节点可以位于右子树或左子树。
- 完美二叉树:所有节点必须有 0 个或 2 个节点,并且所有叶节点应位于同一级别或同一高度。上面满二叉树结构的例子不是完美二叉树,因为节点 6 和节点 1、2、3 不在同一高度。但完全二叉树的例子是完美二叉树。
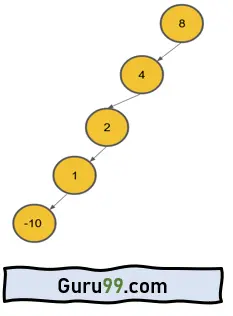
- 退化二叉树:每个节点只能有一个子节点。搜索、插入和删除等所有操作都需要 O(N) 时间。
- 平衡二叉树:在此二叉树中,左右子树的高度差最多为 1。因此,在添加或删除节点时,我们需要再次平衡树的高度。这种自平衡二叉树称为 AVL 树。
BST 有三个基本操作。下面将详细讨论这些。
用 C 和 C++ 实现二叉树
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int value;
struct Node *left, *right;
}
struct Node *getEmptynode(int val)
{
struct Node *tempNode = (struct Node *)malloc(sizeof(struct Node));
tempNode->value = val;
tempNode->left = NULL;
tempNode->right = NULL;
return tempNode;
}
struct Node *successor(struct Node *node)
{
struct Node *present = node;
// going to the left most node
while (present != NULL && present->left != NULL)
{
present = present->left;
}
return present;
}
struct Node *insert(struct Node *node, int value)
{
if (node == NULL)
{
return getEmptynode(value);
}
if (value < node->value)
{
node->left = insert(node->left, value);
}
else
{
node->right = insert(node->right, value);
}
return node;
}
int searchInBST(struct Node *node, int value)
{
struct Node *current = node;
while (current->value != value)
{
if (current->value > value)
{
current = current->left;
}
else
{
current = current->right;
}
if (current == NULL)
{
return 0;
}
}
return 1;
}
void inorder(struct Node *root)
{
if (root != NULL)
{
inorder(root->left);
cout << root->value << " ";
inorder(root->right);
}
}
struct Node *deleteNode(struct Node *node, int value)
{
if (node == NULL)
{
return node;
}
if (value < node->value)
{
node->left = deleteNode(node->left, value);
}
else if (value > node->value)
{
node->right = deleteNode(node->right, value);
}
else
{
if (node->left == NULL)
{
struct Node *temp = node->right;
free(node);
return temp;
}
else if (node->right == NULL)
{
struct Node *temp = node->left;
free(node);
return temp;
}
struct Node *temp = successor(node->right);
node->value = temp->value;
node->right = deleteNode(node->right, temp->value);
}
return node;
}
int main()
{
struct Node *root = NULL;
root = insert(root, 8);
root = insert(root, 4);
root = insert(root, 12);
root = insert(root, 2);
root = insert(root, 6);
root = insert(root, 10);
root = insert(root, 14);
root = insert(root, 1);
root = insert(root, 3);
root = insert(root, 5);
root = insert(root, 7);
root = insert(root, 9);
root = insert(root, 11);
root = insert(root, 13);
root = insert(root, 15);
cout << "InOrder Traversal after inserting all nodes: " << endl;
inorder(root);
root = insert(root, -10);
cout << "\nInOrder Traversal after inserting -10 : " << endl;
inorder(root);
cout << "\nSearching -5 in the BST: " << searchInBST(root, -5) << endl;
cout << "Searching -10 in the BST: " << searchInBST(root, -10) << endl;
root = deleteNode(root,8);
cout<<"After deleting node 8, inorder traversal: "<<endl;
inorder(root);
root = deleteNode(root,-10);
cout<<"\nAfter deleting node -10, inorder traversal: "<<endl;
inorder(root);
}
输出
InOrder Traversal after inserting all nodes: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 InOrder Traversal after inserting -10 : 10 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Searching -5 in the BST: 0 Searching -10 in the BST: 1 After deleting node 8, inorder traversal: -10 1 2 3 4 5 6 7 9 10 11 12 13 14 15 After deleting node -10, inorder traversal: 1 2 3 4 5 6 7 9 10 11 12 13 14 15
用 Python 实现二叉树
class Node:
def __init__(self,value):
self.left = None
self.right = None
self.value = value
def insert(root,value):
if root == None:
return Node(value)
if value< root.value:
root.left = insert(root.left,value)
else:
root.right = insert(root.right,value)
return root
def searchInBST(root,value):
current = root
while current.value != value:
if current.value > value:
current = current.left
else:
current = current.right
if current == None:
return "Not found"
return "Found"
def inorder(root):
if root != None:
inorder(root.left)
print(root.value,end=" ")
inorder(root.right)
def successor(root):
present = root
while present != None and present.left != None:
present = present.left
return present
def deleteNode(root,value):
if root == None:
return root
if value < root.value:
root.left = deleteNode(root.left, value)
elif value>root.value:
root.right = deleteNode(root.right, value)
else:
if root.left == None:
temp = root.right
root = None
return temp
elif root.right == None:
temp = root.left
root = None
return temp
temp = successor(root.right)
root.value = temp.value
root.right = deleteNode(root.right, temp.value)
return root
root = Node(8)
root = insert(root, 4)
root = insert(root, 12)
root = insert(root, 2)
root = insert(root, 6)
root = insert(root, 10)
root = insert(root, 14)
root = insert(root, 1)
root = insert(root, 3)
root = insert(root, 5)
root = insert(root, 7)
root = insert(root, 9)
root = insert(root, 11)
root = insert(root, 13)
root = insert(root, 15)
print("InOrder Traversal after inserting all nodes: ")
inorder(root)
root = insert(root, -10)
print("\nInOrder Traversal after inserting -10 : ")
inorder(root)
print("\nSearching -5 in the BST: ",searchInBST(root, -5))
print("Searching -5 in the BST: ",searchInBST(root, -10))
root = deleteNode(root,8)
print("After deleting node 8, inorder traversal:")
inorder(root)
root = deleteNode(root,-10)
print("\nAfter deleting node -10, inorder traversal:")
inorder(root)
输出
InOrder Traversal after inserting all nodes 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 InOrder Traversal after inserting -10 : -10 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Searching -5 in the BST: Not found Searching -5 in the BST: Found After deleting node 8, inorder traversal: -10 1 2 3 4 5 6 7 9 10 11 12 13 14 15 After deleting node -10, inorder traversal: 1 2 3 4 5 6 7 9 10 11 12 13 14 15
二叉树的应用
以下是二叉树的一些常见应用
- 按排序顺序组织节点数据
- 用于编程语言库中的映射和集合节点对象。
- 在数据结构中搜索元素
» 学习我们的下一个教程关于 组合算法