树遍历（中序、前序和后序）及示例

作者： Sarah Chen Sarah Chen
时间 - 权威教程 更新于

什么是树遍历？

在树数据结构中，遍历是指以某种特定方式访问节点。有两种遍历方式。通常，这种遍历是基于二叉树的。二叉树意味着每个节点最多可以有 2 个子节点。

二叉树是一种著名的数据结构。还有二叉搜索树（BST）。这种遍历用于多种目的。层序遍历用于计算两个节点之间的深度。还有一种称为“AVL”的树，其中计算节点的高度是必要的。我们可以用数组表示二叉树，但为了优化内存，我们将使用结构和指针来引用下一个节点。

树遍历的类型

正如我们之前讨论了 二叉树，现在我们来讨论各种遍历类型。根据类型，有两种遍历方式。之前我们提到了层序遍历或广度优先遍历的必要性。现在，**深度优先遍历**，如后序遍历，用于删除节点（我们稍后会讨论），前序遍历用于复制二叉树，“中序”遍历则以非递减顺序遍历树。

  • 广度优先遍历
  • 深度优先遍历
  • 前序遍历
  • 后序遍历
  • 中序遍历

广度优先遍历

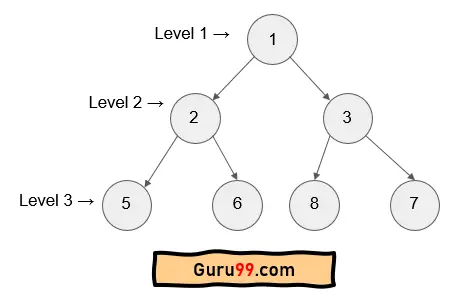
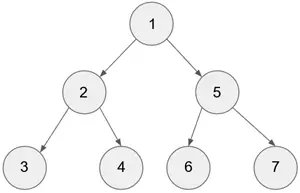
它也被称为层序遍历。让我们考虑下面的树来演示层序遍历。

Breadth-First Traversal

所以，我们将从根节点“1”开始。它将被标记为第 1 层。然后算法将访问当前节点的所有子节点。我们现在将访问节点 2 和 3。它们将被标记为第 2 层。

之后，由于我们有 2 个第 2 层的节点，我们也将访问它们的子节点。所以，我们将访问 5、6、8、7 并将它们标记为第 3 层。这里有一个未提及的点：

节点层级 = 父节点层级 + 1

第 1 层：1

第 2 层：2 3

第 3 层：5 6 8 7

BFS（广度优先搜索）使用类似的算法。

层序遍历的伪代码如下

level_order(node)
Q → Queue()
Q.push(node)
while !Q.empty():
    current_node = Q.pop()
    print current_node.value
# Checking if the current node have any child or not
if current_node.left is not NULL:
    Q.push(current_node.left)
if current_node.right is not NULL:
    Q.push(current_node.right)

二叉树中序遍历

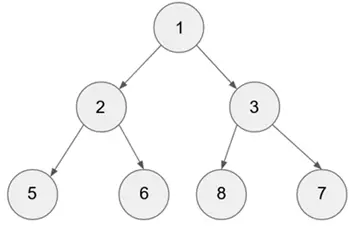
让我们来看和前面一样的例子。在这种遍历类型中，我们首先访问左子树，然后是根，最后是右子树。为了方便记忆，我们可以说中序的顺序是左-根-右。

Inorder Traversal Bianry Tree

对于整个树，假设根是 1。现在算法将遵循

  • 访问节点 1 的左子树。
  • 当前节点是 2（因为它是 1 的左子树）

Inorder Traversal Bianry Tree

  • 访问 2 的左子树。这次当前节点将是 5。
  • 移动到 5，它没有子节点，所以节点 5 将被标记为已访问。它将返回到父节点，即 2。
  • 由于 2 的左子树已被访问，现在也将访问 2。
  • 该 算法 将当前节点移动到节点 2 的右子树，即节点 6。访问节点 6 后。它将移至其父节点 2。
  • 由于节点 2 已被访问，现在我们将访问 2 的父节点，即节点 1。
  • 之后，我们将访问右子树。

所以最终的遍历将如下所示：

中序：5 → 2 → 6 → 1 → 8 → 3 → 7

中序遍历的伪代码如下

InOrder(node):
  if node is not null:
    InOrder(node.left)
  print node.value
    InOrder(node.right)

这是中序遍历的递归算法。对于 二叉搜索树 (BST)，中序遍历会得到排序后的值数组。

相关文章

后序遍历

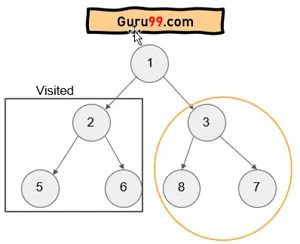
在此遍历中，我们将首先遍历最左边的子树，然后在根之后遍历最右边的子树。所有遍历都将按后序进行。让我们举一个例子

Post-Order Traversal

对于根 = 1，

  • 我们先进入左子树。所以根将变成 2。
  • 然后 2 有左子树，所以我们将进入节点 5。现在根是 5。
  • 它没有左子树，也没有右子树。所以，现在我们将节点 5 标记为已访问，然后移至其父节点。

Post-Order Traversal

  • 现在根是 2，其左子树已完全访问。我们现在将移至其右子树。所以根变成 6。
  • 由于节点 6 没有左子树和右子树，我们将节点 6 标记为已访问，然后移至其父节点 2。
  • 现在，节点 2 的左子树和右子树都已被访问。它也将被标记为已访问。
  • 我们将移至节点 2 的父节点，即节点 1。
  • 对于根 1，左子树已被访问。之后，我们将类似地访问右子树。

Post-Order Traversal

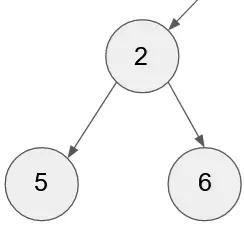
标记的圆圈是右子树。现在我们将访问右子树，就像我们访问左子树一样。之后，我们将访问节点。所以最终的遍历将是

后序：5 → 6 → 2 → 8 → 7 → 3 → 1

后序遍历的伪代码如下

PostOrder(node):
    if node is not null:
       PostOrder(node.left)
       PostOrder(node.right)
       print node.value

前序遍历

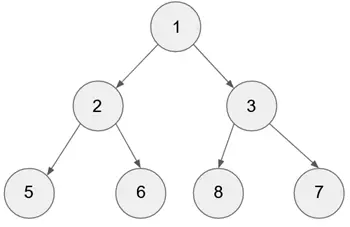
对于前序遍历，算法将首先访问根节点，之后，它将分别移动到左子树和右子树。为了方便理解，我们可以认为前序遍历的访问方式是**根 → 左-右**。

Preorder Traversal

所以，让我们选择节点 1 作为根。

  • 根据算法，首先会访问根，然后是左子树，最后是右子树。
  • 所以，我们将访问根 1。然后我们将移至其左子树。根变成 2。
  • 我们将访问节点 2 并移至其左子树。所以，根变成 3。
  • 我们访问节点 3，然后移至其父节点。现在节点 2 及其左子树已被访问。该访问右子树了。
  • 我们将移至右子树，根变成 4。我们将访问 4。由于 4 没有子节点，我们将移至其父节点。
  • 现在根是 2，它及其左子树和右子树都已被访问。所以，我们将移至其父节点。现在根变成 1。
  • 类似地，我们将访问右子树。

前序：1 → 2 → 3 → 4 → 5 → 6 → 7

后序遍历的伪代码如下

PreOrder(node):
   if node is not null:
     print node.value
         PreOrder(node.left)
         PreOrder(node.right)

Python 实现

class Node:
    def __init__(self, item):
    self.left = None
self.right = None
self.val = item
# creating a tree data structure
def inorder(root):
#checking if the root is null or not
if root:
    inorder(root.left)
# recursively calling left subtree
print(str(root.val) + " ", end = '')
inorder(root.right)
# recursively calling right subtree
def postorder(root):
    if root:
    postorder(root.left)
postorder(root.right)
print(str(root.val) + " ", end = '')
def preorder(root):
    if root:
    print(str(root.val) + " ", end = '')
preorder(root.left)
preorder(root.right)
def levelOrder(root):
    queue = list()
queue.append(root)
while len(queue) & gt;
0:
    current = queue[0]
queue = queue[1: ]
print(str(current.val) + " ", end = "")
if current.left:
    queue.append(current.left)
if current.right:
   queue.append(current.right)
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print("\nLevelOrder traversal:\t", end = " ")
levelOrder(root)
print("\nInorder traversal:\t", end = " ")
inorder(root)
print("\nPreorder traversal:\t", end = " ")
preorder(root)
print("\nPostorder traversal:\t", end = " ")
postorder(root)

输出

LevelOrder traversal:  1 2 3 4 5 6 7
Inorder traversal:     4 2 5 1 6 3 7
Preorder traversal:    1 2 4 5 3 6 7
Postorder traversal:   4 5 2 6 7 3 1

C 语言实现

#include <stdio.h>
#include <stdlib.h>
struct node {
   int value;
   struct node* left;
   struct node* right;
};
// Inorder traversal
void InOrder(struct node* root) {
   if (root == NULL) return;
   InOrder(root->left);
   printf("%d ", root->value);
   InOrder(root->right);
}
// PreOrder traversal
void PreOrder(struct node* root) {
  if (root == NULL) return;
  printf("%d ", root->value);
  PreOrder(root->left);
  PreOrder(root->right);
}
// PostOrder traversal
void PostOrder(struct node* root) {
  if (root == NULL) return;
  PostOrder(root->left);
  PostOrder(root->right);
  printf("%d ", root->value);
}
// Create a new Node
struct node* createNode(int value) {
  struct node* newNode = malloc(sizeof(struct node));
  newNode->value = value;
  newNode->left = NULL;
  newNode->right = NULL;
  return newNode;
}
int main() {
  struct node* root = createNode(1);
  root->left = createNode(2);
  root->right = createNode(3);
  root->left->left = createNode(4);
  root->left->right = createNode(5);
  root->right->left = createNode(6);
  root->right->right = createNode(7);
  printf("Inorder traversal:\t");
  InOrder(root);
  printf("\PreOrder traversal:\t");
  PreOrder(root);
  printf("\nPostOrder traversal:\t");
  PostOrder(root);
}

输出

Inorder traversal: 4 2 5 1 6 3 7
Preorder traversal: 1 2 4 5 3 6 7
Postorder traversal: 4 5 2 6 7 3 1

C++ 实现（使用 std:queue 进行层序遍历）

#include <stdio.h>
#include <stdlib.h>
#include<queue>
typedef struct node {
  int value;
  struct node* left;
  struct node* right;
}node;
// Inorder traversal
void InOrder(struct node* root) {
  if (root == NULL) return;
  InOrder(root->left);
  printf("%d ", root->value);
  InOrder(root->right);
}
// PreOrder traversal
void PreOrder(struct node* root) {
  if (root == NULL) return;
  printf("%d ", root->value);
  PreOrder(root->left);
  PreOrder(root->right);
}
// PostOrder traversal
void PostOrder(struct node* root) {
  if (root == NULL) return;
  PostOrder(root->left);
  PostOrder(root->right);
  printf("%d ", root->value);
}
void LevelOrder(struct node* root){
   std::queue<struct node*> Q;
   Q.push(root);
   while(!Q.empty()){
   struct node* current = Q.front();
   Q.pop();
   printf("%d ",current->value);
 if(current->left)
   Q.push(current->left);
 if(current->right)
   Q.push(current->right);
  }
}
// Create a new Node
struct node* createNode(int value) {
  struct node* newNode = new node();
  newNode->value = value;
  newNode->left = NULL;
  newNode->right = NULL;
  return newNode;
}
int main() {
  struct node* root = createNode(1);
  root->left = createNode(2);
  root->right = createNode(3);
  root->left->left = createNode(4);
  root->left->right = createNode(5);
  root->right->left = createNode(6);
  root->right->right = createNode(7);
  printf("Level Order traversal:\t");
  LevelOrder(root);
  printf("\nInorder traversal:\t");
  InOrder(root);
  printf("\nPreOrder traversal:\t");
  PreOrder(root);
  printf("\nPostOrder traversal:\t");
  PostOrder(root);
}

LevelOrder traversal:  1 2 3 4 5 6 7
Inorder traversal:     4 2 5 1 6 3 7
Preorder traversal:    1 2 4 5 3 6 7
Postorder traversal:   4 5 2 6 7 3 1