插入排序:C、C++、Java、Python 示例算法
什么是插入排序?
插入排序是一种比较排序算法,它通过一次迭代一个元素并将该元素放置在其正确位置来对元素进行排序。
每个元素都会被依次插入到一个已经排序好的列表中。最初,已排序列表的大小为一。插入排序算法确保在第 k 次迭代后,前 k 个元素都是有序的。
插入排序算法的特性
插入排序算法具有以下重要特性:
- 它是一种稳定的排序技术,因此不会改变相等元素的相对顺序。
- 它对较小的数据集效率很高,但对较大的列表效果不佳。
- 插入排序是自适应的,如果输入部分有序,它会减少总步骤数。将 数组 作为输入以提高效率。
插入操作如何工作?
在插入排序算法中,插入操作用于排序未排序的元素。它有助于将新元素插入到已排序的列表中。
插入操作的伪代码
考虑一个包含 N 个元素的列表 A。
A[N-1] is the element to be inserted in the sorted sublist A[0..N-2]. For i = N-1 to 1: if A[i] < A[i-1], then swap A[i] and A[i-1] else Stop
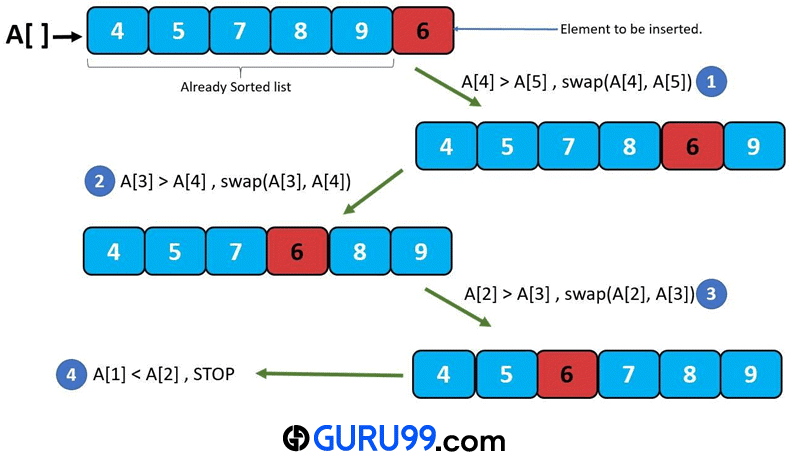
在上面的示例中,新元素 6 需要插入到一个已排序的列表中。
步骤 1) 与 A[5] 的相邻左侧元素 9 比较,9 > 6,我们交换 9 和 6 的位置。现在元素 6 已移至 A[4]。
步骤 2) 现在,我们比较 A[4] 和 A[3],发现 A[3] > A[4],我们再次交换 6 和 8 的位置。
步骤 3) 现在比较 A[3] 和 A[2],因为 A[2] > A[3],交换 7 和 6 的位置。
步骤 4) 我们比较 A[1] 和 A[2],因为 A[1] < A[2],即相邻的左侧元素不再大于。现在我们得出结论,6 已正确插入,我们在此停止算法。
插入排序如何工作
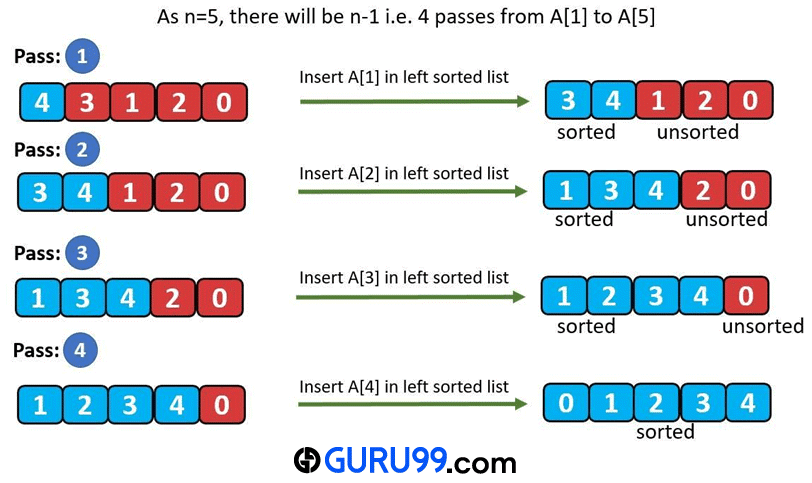
上面讨论的插入操作是插入排序的基石。插入过程应用于每个元素,最后,我们得到排序后的列表。
上面的示例图演示了插入排序在数据结构中的工作原理。最初,已排序的子列表中只有一个元素,即 4。插入 A[1],即 3 之后,已排序子列表的大小增加到 2。
C++ 插入排序程序
#include <iostream>
using namespace std;
int main(){
//unsorted list
int unsorted[] = {9,8,7,6,5,4,3,3,2,1};
//size of list
int size_unsorted = sizeof(unsorted) / sizeof(unsorted[0]);
//printing unsorted list
cout << "\nUnsorted: ";
for(int i = 0 ; i < size_unsorted ; i++){
cout << unsorted[i] << " ";
}
int current_element,temp;
for(int i = 1; i < size_unsorted; i++){
current_element = unsorted[i];
for(int j = i-1; j >= 0 && unsorted[j] > current_element; j--){
//swapping if current element is lesser
temp = unsorted[j+1];
unsorted[j+1] = unsorted[j];
unsorted[j] = temp;
}
}
//printing sorted list
cout << "\nSorted: ";
for(int i = 0 ; i < size_unsorted ; i++){
cout << unsorted[i] << " ";
}
return 0;
}
输出
Unsorted: 9 8 7 6 5 4 3 3 2 1 Sorted: 1 2 3 3 4 5 6 7 8 9
C 语言插入排序代码
#include <stdio.h>
int main() {
//unsorted list
int unsorted[] = {9,8,7,6,5,4,3,3,2,1};
//size of list
int size_unsorted = sizeof(unsorted) / sizeof(unsorted[0]);
//printing unsorted list
printf("\nUnsorted: ");
for(int i = 0 ; i < size_unsorted ; i++){
printf("%d ", unsorted[i]);
}
int current_element, temp;
for(int i = 1; i < size_unsorted; i++){
current_element = unsorted[i];
for(int j = i-1; j >= 0 && unsorted[j] > current_element; j--){
//swapping if current element is lesser
temp = unsorted[j+1];
unsorted[j+1] = unsorted[j];
unsorted[j] = temp;
}
}
//printing sorted list
printf("\nSorted: ");
for(int i = 0 ; i < size_unsorted ; i++){
printf("%d ", unsorted[i]);
}
return 0;
}
输出
Output: Unsorted: 9 8 7 6 5 4 3 3 2 1 Sorted: 1 2 3 3 4 5 6 7 8 9
Python 插入排序程序
#unsorted list
unsorted = [9,8,7,6,5,4,3,3,2,1]
#size of list
size_unsorted = len(unsorted)
#printing unsorted list
print("\nUnsorted: ", end="")
for i in range(size_unsorted):
print(unsorted[i], end=" ")
for i in range(1, size_unsorted):
current_element = unsorted[i]
j = i - 1
while j >= 0 and unsorted[j] > current_element:
#swapping if current element is lesser
unsorted[j+1], unsorted[j] = unsorted[j], unsorted[j+1]
j -= 1
#printing sorted list
print("\nSorted: ", end="")
for i in range(size_unsorted):
print(unsorted[i], end=" ")
输出
Unsorted: 9 8 7 6 5 4 3 3 2 1 Sorted: 1 2 3 3 4 5 6 7 8 9
插入排序的属性
以下是插入排序的重要属性:
- 在线:插入排序可以在接收到元素时进行排序。也就是说,如果我们已经对一个元素列表进行了排序,然后向列表中添加了更多元素,那么就不需要重新运行整个排序过程。相反,我们只需要迭代新添加的元素。
- 就地:插入排序算法的空间复杂度是常数,不需要额外的空间。该算法就地排序元素。
- 稳定:在插入排序中,如果元素的数值相等,我们不会交换它们。例如,如果 x 和 y 两个元素相等,并且 x 在未排序列表中出现在 y 之前,那么在排序列表后,x 将出现在 y 之前。这使得插入排序稳定。
- 自适应:如果输入元素或元素子集已排序,则 排序算法 是自适应的。如上所述,插入排序的最佳运行时间为 O(N),最坏运行时间为 O(N^2)。插入排序是一种自适应排序算法。
插入排序的复杂度
空间复杂度
插入排序不需要额外的空间来排序元素,空间复杂度是常数,即 O(1)。
时间复杂度
由于插入排序同时迭代每个元素,因此需要 N-1 次传递来排序 N 个元素。对于每次传递,如果元素已排序,它可能需要零次交换,或者如果元素按降序排列,则需要交换。
- 对于第 1 次传递,所需的最小交换次数为零,最大交换次数为 1。
- 对于第 2 次传递,所需的最小交换次数为零,最大交换次数为 2。
- 对于第 N 次传递,所需的最小交换次数为零,最大交换次数为 N。
- 最小交换次数为零,因此最佳时间复杂度为 O(N)(迭代 N 次传递)。
- 总最大交换次数为 (1+2+3+4+..+N) i.e. N(N+1)/2,最坏时间复杂度为 O(N^2)。
以下是插入排序的重要时间复杂度:
- 最坏情况复杂度:O(n^2):当数组已按升序排列时,将其按降序排序是最坏情况。
- 最佳情况复杂度:O(n):最佳情况复杂度发生在数组已排序时,外层循环运行 n 次,而内层循环根本不运行。只有 n 次比较。因此,在这种情况下,复杂度是线性的。
- 平均情况复杂度:O(n^2):这发生在数组的元素以混乱的顺序出现时,既不是升序也不是降序。
摘要
- 插入排序是一种基于比较的排序算法方法。
- 它是一种稳定的排序技术,因此不会改变相等元素的相对顺序。
- 在每个元素上,插入操作用于将元素插入到已排序的子列表中。
- 插入排序是一种就地排序算法。
- 插入排序的最坏和平均时间复杂度是二次的,即 O(N^2)。
- 插入排序不需要任何辅助空间。