贪心算法及示例：是什么、方法和途径

作者： Sarah Chen Sarah Chen
时间 - 权威教程 更新于

什么是贪心算法？

在贪心算法中，一组资源根据在执行的任何给定阶段该资源的 maximum、immediate availability 进行递归划分。

要基于贪心方法解决问题，有两个阶段

  1. 扫描项目列表
  2. 优化

在本次贪心算法教程中，这些阶段在数组的划分过程中并行进行。

要理解贪心方法，您需要具备递归和上下文切换的实际操作知识。这有助于您理解代码的跟踪方式。您可以用自己必需且充分的陈述来定义贪心范式。

有两个条件定义了贪心范式。

  • 每个步骤的解决方案都必须将问题构建成其最佳可接受的解决方案。
  • 如果问题的构建可以在有限的贪心步骤内停止，则就足够了。

随着理论的不断发展，让我们来描述与贪心搜索方法相关的历史。

贪心算法的历史

以下是贪心算法的一个重要里程碑

  • 贪心算法是在 20 世纪 50 年代为许多图遍历算法概念化的。
  • Esdger Djikstra 提出了生成最小生成树的算法。他旨在缩短荷兰首都阿姆斯特丹的路线跨度。
  • 在同一十年中，Prim 和 Kruskal 实现了基于最小化加权路线成本的优化策略。
  • 在 70 年代，美国研究人员 Cormen、Rivest 和 Stein 在他们经典的算法导论书中提出了贪心解决方案的递归子结构。
  • 贪心搜索范式于 2005 年在美国国家标准与技术研究院 (NIST) 的记录中注册为一种不同类型的优化策略。
  • 至今，运行网络的协议，如开放最短路径优先 (OSPF) 和许多其他网络数据包交换协议，都使用贪心策略来最大限度地减少在网络上花费的时间。

贪心策略和决策

逻辑最简单的形式被归结为“贪心”或“非贪心”。这些陈述由每个算法阶段所采取的前进方法来定义。

例如，Djikstra 的算法利用了分步贪心策略，通过计算成本函数来识别互联网上的主机。成本函数返回的值决定了下一条路径是“贪心”还是“非贪心”。

简而言之，如果一个算法在任何阶段都采取了不局部贪心的步骤，那么它就不是贪心的。贪心问题会在没有进一步贪心范围的情况下停止。

贪心算法的特点

贪心算法的重要特点是

  • 有一个有序的资源列表，带有成本或价值属性。这些量化了系统的约束。
  • 在约束适用的时间内，您将获取最多数量的资源。
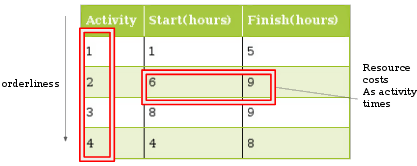
  • 例如，在活动调度问题中，资源成本以小时为单位，并且活动需要按顺序执行。

Characteristics of the Greedy Algorithm

为什么要使用贪心方法？

以下是使用贪心方法的原因

  • 贪心方法有一些权衡，这可能使其适合优化。
  • 一个突出的原因是立即获得最可行的解决方案。在活动选择问题（下文解释）中，如果可以在当前活动完成之前完成更多活动，则这些活动可以在同一时间内执行。
  • 另一个原因是根据条件递归地划分问题，而无需组合所有解决方案。
  • 在活动选择问题中，“递归划分”步骤是通过仅扫描一次项目列表并考虑特定活动来实现的。

如何解决活动选择问题

在活动调度示例中，每个活动都有一个“开始”和“结束”时间。每个活动都通过一个数字进行索引以供参考。有两种活动类别。

  1. 已考虑的活动：是活动，它是分析执行更多剩余活动的能力的参考。
  2. 剩余活动：一个或多个索引在已考虑活动之前的活动。

总持续时间是执行活动的成本。即（结束时间 - 开始时间）给我们活动持续时间作为成本。

您将了解到，贪心程度是您在已考虑活动的时间内可以执行的剩余活动的数量。

相关文章

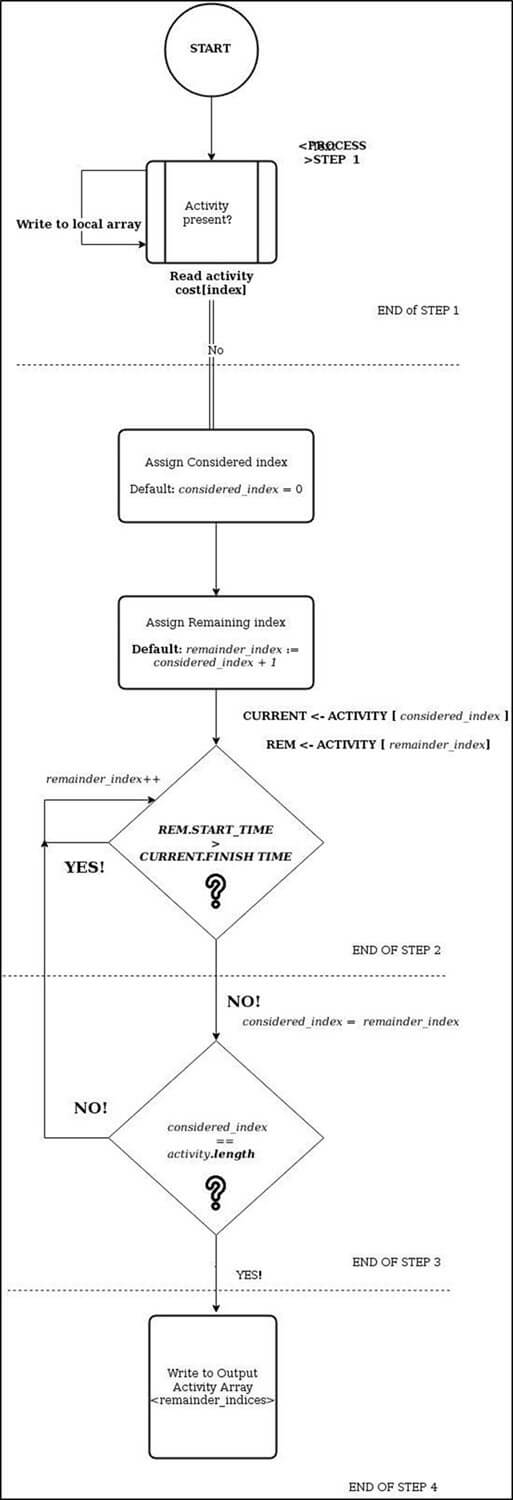
贪心方法的架构

步骤 1） 扫描活动成本列表，从索引 0 开始作为已考虑的索引。

步骤 2） 当在已考虑活动完成之前可以完成更多活动时，开始寻找一个或多个剩余活动。

步骤 3） 如果没有剩余活动了，则当前剩余活动成为下一个已考虑的活动。用新的已考虑活动重复步骤 1 和步骤 2。如果没有剩余活动了，请转到步骤 4。

步骤 4） 返回已考虑索引的并集。这些是用于最大化吞吐量的活动索引。

Architecture of the Greedy Approach
贪心方法的架构

代码解释

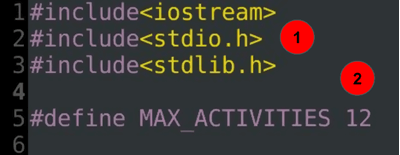
#include<iostream>
#include<stdio.h>
#include<stdlib.h>

#define MAX_ACTIVITIES 12

Architecture of the Greedy Approach

代码解释

  1. 包含的头文件/类
  2. 用户提供的最大活动数量。
using namespace std;

class TIME
{
    public:
    int hours;

    public: TIME()
    {
   	 hours = 0;
    }
};

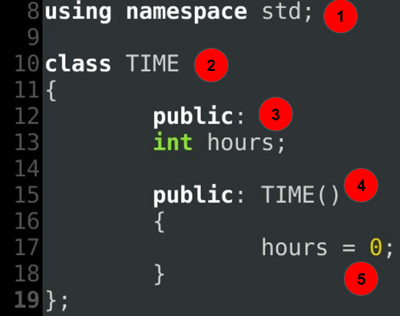
Architecture of the Greedy Approach

代码解释

  1. 流操作的命名空间。
  2. TIME 的类定义
  3. 小时时间戳。
  4. TIME 默认构造函数
  5. 小时变量。
class Activity
{
    public:
    int index;
    TIME start;
    TIME finish;

    public: Activity()
    {
   	 start = finish = TIME();
    }
};

Architecture of the Greedy Approach

代码解释

  1. activity 的类定义
  2. 定义持续时间的时间戳
  3. 所有时间戳在默认构造函数中均初始化为 0
class Scheduler
{
    public:
    int considered_index,init_index;
    Activity *current_activities = new    Activity[MAX_ACTIVITIES];
    Activity *scheduled;

Architecture of the Greedy Approach

代码解释

  1. 调度器类定义的第一部分。
  2. 已考虑索引是扫描 数组 的起点。
  3. 初始化索引用于分配随机时间戳。
  4. 使用 new 运算符动态分配活动对象的数组。
  5. 调度指针定义了贪心的当前基本位置。
Scheduler()
{
   	 considered_index = 0;
   	 scheduled = NULL;
...
...

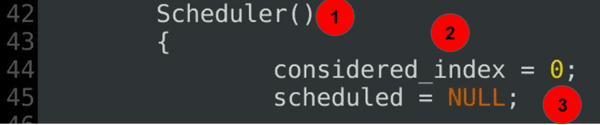
Architecture of the Greedy Approach

代码解释

  1. 调度器构造函数 – 调度器类定义的第二部分。
  2. 已考虑索引定义了当前扫描的当前开始。
  3. 当前贪心程度在开始时未定义。
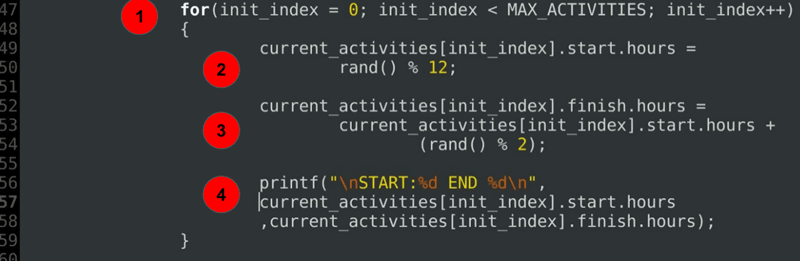
for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++)
 {
   		 current_activities[init_index].start.hours =
   			 rand() % 12;

   		 current_activities[init_index].finish.hours =
   			 current_activities[init_index].start.hours +
   				 (rand() % 2);

   		 printf("\nSTART:%d END %d\n",
   		 current_activities[init_index].start.hours
   		 ,current_activities[init_index].finish.hours);
 }
…
…

Architecture of the Greedy Approach

代码解释

  1. 一个 for 循环，用于初始化当前调度的每个活动的开始时间和结束时间。
  2. 开始时间初始化。
  3. 结束时间初始化始终在开始时间之后或正好在开始时间。
  4. 一个用于打印分配时间段的调试语句。
	public:
   		 Activity * activity_select(int);
};

Architecture of the Greedy Approach

代码解释

  1. 第 4 部分 – 调度器类定义的最后一部分。
  2. Activity select 函数接受一个起始点索引作为基准，并将贪心搜索划分为贪心子问题。
Activity * Scheduler :: activity_select(int considered_index)
{
    this->considered_index = considered_index;
    int greedy_extent = this->considered_index + 1;
…
…

Architecture of the Greedy Approach

  1. 使用范围解析运算符（::），提供了函数定义。
  2. 已考虑索引是通过值调用的索引。greedy_extent 是初始化在已考虑索引之后的一个索引。
Activity * Scheduler :: activity_select(int considered_index)
{
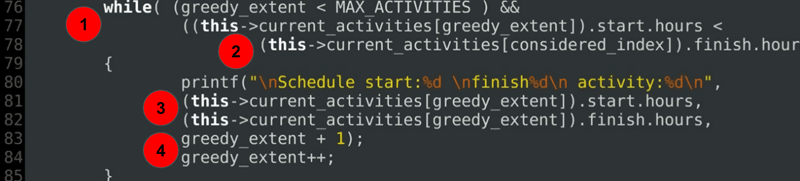
    	while( (greedy_extent < MAX_ACTIVITIES ) &&
   	 ((this->current_activities[greedy_extent]).start.hours <
   		 (this->current_activities[considered_index]).finish.hours ))
    	{
   	 printf("\nSchedule start:%d \nfinish%d\n activity:%d\n",
   	 (this->current_activities[greedy_extent]).start.hours,
   	 (this->current_activities[greedy_extent]).finish.hours,
   	 greedy_extent + 1);
   	 greedy_extent++;
    	}
…
...

Architecture of the Greedy Approach

代码解释

  1. 核心逻辑——贪心程度受限于活动数量。
  2. 检查当前活动的开始时间是否可以在已考虑的活动（由已考虑索引给出）完成之前安排。
  3. 只要有可能，就会打印一个可选的调试语句。
  4. 前进到活动数组的下一个索引
...
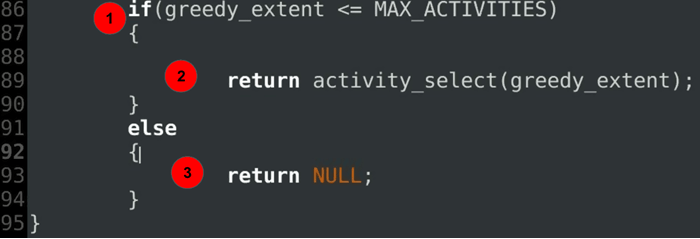
if ( greedy_extent <= MAX_ACTIVITIES )
    {

   	 return activity_select(greedy_extent);
    }
    else
    {
   	 return NULL;
    }
}

Architecture of the Greedy Approach

代码解释

  1. 条件检查是否已覆盖所有活动。
  2. 如果未覆盖，您可以使用已考虑索引作为当前点重新启动贪心。这是一个递归步骤，可以贪婪地划分问题陈述。
  3. 如果覆盖了，则返回调用者，没有扩展贪心的范围。
int main()
{
    Scheduler *activity_sched = new Scheduler();
    activity_sched->scheduled = activity_sched->activity_select(
   				activity_sched->considered_index);
    return 0;
}

Architecture of the Greedy Approach

代码解释

  1. 用于调用调度器的 main 函数。
  2. 实例化了一个新的调度器。
  3. activity select 函数（返回 activity 类型指针）在贪心搜索结束后返回给调用者。

输出

START:7 END 7

START:9 END 10

START:5 END 6

START:10 END 10

START:9 END 10

Schedule start:5 
finish6
 activity:3

Schedule start:9 
finish10
 activity:5

贪心技术的局限性

它不适用于需要为每个子问题（如排序）提供解决方案的贪心问题。

因此，在这些贪心算法实践问题中，贪心方法可能是错误的；在最坏的情况下，甚至可能导致非最优解。

因此，贪心算法的缺点是不知道当前贪心状态之后会发生什么。

以下是贪心方法缺点的说明

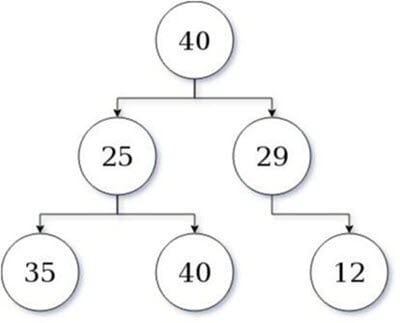
Limitations of Greedy Technique

在下图所示的树（值越高，贪心越强）中，算法状态为值 40，很可能会选择 29 作为下一个值。此外，它的搜索以 12 结束。这相当于价值 41。

然而，如果算法采取了次优路径或采用了征服策略。那么 25 将跟随 40，整体成本改进将为 65，这比次优决策高出 24 分。

贪心算法示例

大多数网络算法都使用贪心方法。以下是一些贪心算法的示例列表

  • Prim 的最小生成树算法
  • 旅行商问题
  • 图 – 地图着色
  • Kruskal 的最小生成树算法
  • Dijkstra 的最小生成树算法
  • 图 – 顶点覆盖
  • 背包问题
  • 作业调度问题

摘要

总结来说，本文定义了贪心范式，展示了贪心优化和递归如何帮助您获得最佳解决方案。贪心算法已广泛应用于多种语言的问题解决中，例如 Greedy algorithm Python、C、C#、PHP、Java 等。贪心算法的活动选择示例被描述为一个可以通过贪心方法实现最大吞吐量的战略性问题。最后，解释了使用贪心方法的缺点。