0/1 背包问题使用动态规划示例修复
Sarah Chen 什么是背包问题？
背包问题算法在组合数学中是一个非常有用的问题。在超市里有 n 个包裹（n ≤ 100），包裹 i 的重量是 W[i] ≤ 100，价值是 V[i] ≤ 100。一个小偷闯入超市，小偷不能携带超过 M 的重量（M ≤ 100）。要解决的问题是：小偷会拿走哪些包裹才能获得最高价值？
输入
- 最大重量 M 和包裹数量 n。
- 重量数组 W[i] 和对应的价值 V[i]。
输出
- 在容量内最大化价值和对应重量。
- 小偷会拿走哪些包裹。
背包算法还可以进一步分为两种类型
- 使用动态规划的 0/1 背包问题。在这种背包算法类型中，每个包裹都可以拿走或不拿走。此外，小偷不能拿走已拿走包裹的一部分，也不能拿走同一个包裹多次。这种类型可以用动态规划方法解决。
- 分数背包问题算法。这种类型可以用贪心策略解决。
如何使用动态规划和示例解决背包问题
在分治策略中，您将要解决的问题划分为子问题。子问题进一步划分为更小的子问题。该任务将继续进行，直到您获得可以轻松解决的子问题。但是，在这样的划分过程中，您可能会多次遇到相同的问题。
背包动态规划的基本思想是使用一个表来存储已解决子问题的解决方案。如果您再次遇到子问题，只需从表中获取解决方案，而无需再次解决它。因此，由动态规划设计的算法非常有效。
要通过动态规划解决问题，您需要执行以下任务
- 找到最小子问题的解决方案。
- 找出通过更小的子问题的解决方案来构建子问题解决方案的公式（或规则）。
- 创建一个存储子问题解决方案的表。然后根据找到的公式计算子问题的解决方案并保存到表中。
- 从已解决的子问题中，您找到原始问题的解决方案。
分析 0/1 背包问题
在使用动态规划分析 0/1 背包问题时，您可以发现一些值得注意的点。背包算法的价值取决于两个因素
- 正在考虑的包裹数量
- 背包可以存储的剩余重量。
因此，您有两个可变数量。
使用动态规划，您有有用的信息
- 目标函数将取决于两个可变数量
- 选项表将是一个二维表。
如果 B[i][j] 是在 {1, 2, …, i} 的包裹中选择并限制重量为 j 的最大可能价值。
- 在 n 个包裹中选择，重量限制为 M 的最大价值是 B[n][M]。换句话说：当有 i 个包裹可供选择时，B[i][j] 是当背包的最大重量为 j 时的最佳重量。
- 最优重量始终小于或等于最大重量：B[i][j] ≤ j。
例如：B[4][10] = 8。这意味着在最佳情况下，所选包裹的总重量为 8，当有前 4 个包裹可供选择（第 1 至第 4 个包裹）并且背包的最大重量为 10。并非所有 4 个物品都必须被选中。
计算 B[i][j] 的公式
输入，您定义
- W[i]、V[i] 分别是包裹 i 的重量和价值，其中 i
![计算 B[i][j] 的公式](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%2016%2023'%3E%3C/svg%3E)
{1, …, n}。 - M 是背包可以携带的最大重量。
![计算 B[i][j] 的公式](https://guru99.com.cn/images/1/043019_0611_KnapsackPro4.png){kind=small}
{1, …, n}。在只有 1 个包裹可供选择的情况下。您计算每个 j 的 B[1][j]：这意味着背包的最大重量 ≥ 第 1 个包裹的重量
B[1][j] = W[1]
在重量限制为 j 的情况下，在 {1, 2, …, i – 1, i} 的包裹中进行选择的最优选择将有两种可能性
- 如果未选择包裹 i，B[i][j] 是在 {1, 2, …, i – 1} 的包裹中选择并限制重量为 j 的最大可能价值。您有
B[i][j] = B[i – 1][j]
- 如果选择了包裹 i（当然，只有在 W[i] ≤ j 时才考虑这种情况），则 B[i][j] 等于包裹 i 的价值 V[i] 加上在 {1, 2, …, i – 1} 的包裹中选择并限制重量为 (j – W[i]) 的最大价值。也就是说，在价值方面，您有
B[i][j] = V[i] + B[i – 1][j – W[i]]
由于创建了 B[i][j]，它是最大可能价值，B[i][j] 将是上述 2 个值的最大值。
动态规划的基础
所以，您需要考虑选择包裹 i 是否更好。从中您得到递归公式如下
B[i][j]= max(B[i – 1][j], V[i]+B[i – 1][j – W[i]]
很容易看出 B[0][j] = 从 0 个包裹中选择的最大可能价值 = 0。
计算选项表
您根据上述递归公式构建一个选项表。检查结果是否正确（如果不正确，则重新构建目标函数 B[i][j]）。通过创建目标函数 B[i][j] 和选项表，您将指导跟踪。
选项表 B 包含 n + 1 行，M + 1 列，
- 首先，填充动态规划的基础：第 0 行包含所有零。
- 使用递归公式，使用第 0 行计算第 1 行，使用第 1 行计算第 2 行，依此类推……直到计算完所有行。
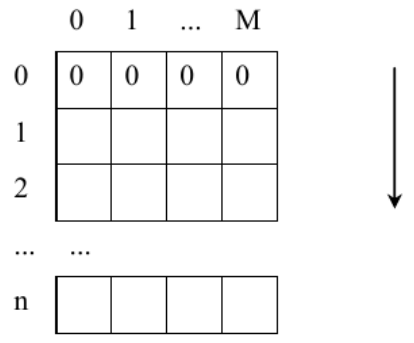
追踪
在计算选项表时，您对 B[n][M] 感兴趣，这是在所有 n 个包裹中选择且重量限制为 M 时获得的最大价值。
- 如果 B[n][M] = B[n – 1][M]，则未选择第 n 个包裹，您跟踪 B[n – 1][M]。
- 如果 B[n][M] ≠ B[n – 1][M]，则您会注意到最优选择包含第 n 个包裹，并跟踪 B[n – 1][M – W[n]]。
继续跟踪，直到到达选项表的第 0 行。
查找选项表以确定所选包裹的算法
注意：如果 B[i][j] = B[i – 1][j]，则未选择第 i 个包裹。B[n][W] 是放入背包的包裹的最优总价值。
跟踪步骤
- 步骤 1：从 i = n，j = M 开始。
- 步骤 2：在列 j 中，从底部向上，找到行 i，使得 B[i][j] > B[i – 1][j]。标记选中的包裹 i：Select [i] = true；
- 步骤 3：j = B[i][j] – W[i]。如果 j > 0，转到步骤 2，否则转到步骤 4
- 步骤 4：根据选项表打印选中的包裹。
Java 代码
public void knapsackDyProg(int W[], int V[], int M, int n) {
int B[][] = new int[n + 1][M + 1];
for (int i=0; i<=n; i++)
for (int j=0; j<=M; j++) {
B[i][j] = 0;
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= M; j++) {
B[i][j] = B[i - 1][j];
if ((j >= W[i-1]) && (B[i][j] < B[i - 1][j - W[i - 1]] + V[i - 1])) {
B[i][j] = B[i - 1][j - W[i - 1]] + V[i - 1];
}
System.out.print(B[i][j] + " ");
}
System.out.print("\n");
}
System.out.println("Max Value:\t" + B[n][M]);
System.out.println("Selected Packs: ");
while (n != 0) {
if (B[n][M] != B[n - 1][M]) {
System.out.println("\tPackage " + n + " with W = " + W[n - 1] + " and Value = " + V[n - 1]);
M = M - W[n-1];
}
n--;
}
}
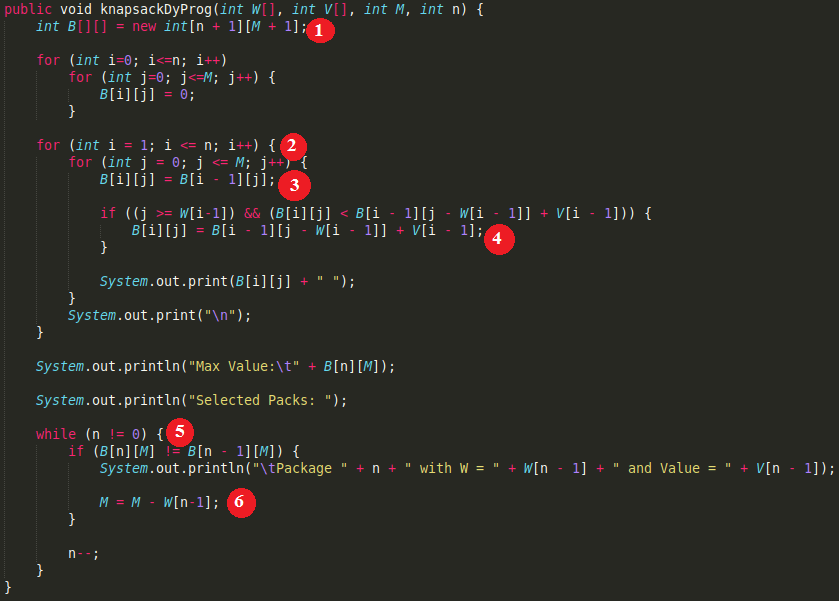
背包代码说明
- 创建表 B[][]。将每个单元格的默认值设置为 0。
- 以自底向上的方式构建表 B[][]。使用检索公式计算选项表。
- 计算 B[i][j]。如果您不选择包裹 i。
- 然后评估：如果您选择包裹 i，它将更有益，然后重置 B[i][j]。
- 从第 n 行到第 0 行跟踪表。
- 如果您选择包裹 n。一旦选择包裹 n，只能添加重量 M – W[n – 1]。
在本教程中，您有两个示例。这是运行上述程序并附带两个示例的 Java 代码
public void run() {
/*
* Pack and Weight - Value
*/
//int W[] = new int[]{3, 4, 5, 9, 4};
int W[] = new int[]{12, 2, 1, 1, 4};
//int V[] = new int[]{3, 4, 4, 10, 4};
int V[] = new int[]{4, 2, 1, 2, 10};
/*
* Max Weight
*/
//int M = 11;
int M = 15;
int n = V.length;
/*
* Run the algorithm
*/
knapsackDyProg(W, V, M, n);
}
您有输出
- 第一个例子
0 0 0 3 3 3 3 3 3 3 3 3 0 0 0 3 4 4 4 7 7 7 7 7 0 0 0 3 4 4 4 7 7 8 8 8 0 0 0 3 4 4 4 7 7 10 10 10 0 0 0 3 4 4 4 7 8 10 10 11 Max Value: 11 Selected Packs: Package 5 with W = 4 and Value = 4 Package 2 with W = 4 and Value = 4 Package 1 with W = 3 and Value = 3
- 第二个示例
0 0 0 0 0 0 0 0 0 0 0 0 4 4 4 4 0 0 2 2 2 2 2 2 2 2 2 2 4 4 6 6 0 1 2 3 3 3 3 3 3 3 3 3 4 5 6 7 0 2 3 4 5 5 5 5 5 5 5 5 5 6 7 8 0 2 3 4 10 12 13 14 15 15 15 15 15 15 15 15 Max Value: 15 Selected Packs: Package 5 with W = 4 and Value = 10 Package 4 with W = 1 and Value = 2 Package 3 with W = 1 and Value = 1 Package 2 with W = 2 and Value = 2
