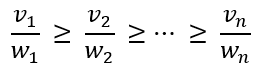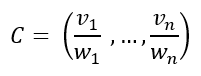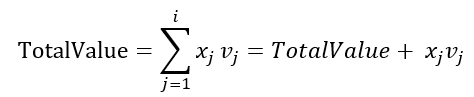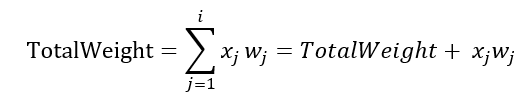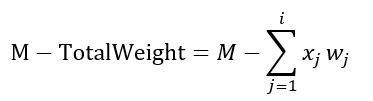分数背包问题:贪心算法及示例
什么是贪心策略?
贪心算法类似于动态规划算法,通常用于解决最优问题(根据特定标准找到问题的最佳解决方案)。
贪心算法通过实施最优的局部选择,希望这些选择能够为要解决的问题带来最优的全局解决方案。贪心算法通常不难设置,速度快(时间复杂度通常是线性函数或非常接近二次函数)。此外,这些程序也不难调试,内存占用少。但结果不总是最优解。
贪心策略常用于通过构建选项A来解决组合优化问题。选项A通过选择A的每个组件Ai直到完成(足够n个组件)来构建。对于每个Ai,你都会选择最优的Ai。这样,在最后一步可能一无所获,只能接受最后一个剩余的值。
贪心决策有两个关键组成部分
- 贪心选择的方式。你可以选择当前最佳的解决方案,然后解决由最后一次选择所产生的子问题。贪心算法的选择可能取决于之前的选择。但它不能依赖于任何未来的选择,也不能依赖于子问题的解决方案。算法以循环方式进行选择,同时将给定问题缩小为更小的子问题。
- 最优子结构。如果一个问题的最优解包含其子问题的最优解,那么该问题就具有最优子结构。
贪心算法有五个组成部分
- 一组候选者,从中创建解决方案。
- 一个选择函数,用于选择最佳候选者添加到解决方案中。
- 一个可行函数,用于决定是否可以使用候选者来构建解决方案。
- 一个目标函数,用于确定解决方案或不完整解决方案的值。
- 一个评估函数,用于指示何时找到完整解决方案。
贪心一号的思路
有了第一个思路,贪心一号的步骤如下
- 按值非递增顺序排序。
- 依次考虑排序后的包裹,如果背包的剩余容量足够容纳该包裹(即放入背包的包裹总重量加上考虑的包裹重量不超过背包容量),则将考虑的包裹放入背包。
然而,这种贪心算法并非总是能给出最优解。这里有一个反例
- 问题参数:n = 3;M = 19。
- 包裹:{i = 1; W[i] = 14; V[i] = 20}; {i = 2; W[i] = 6; V[i] = 16}; {i = 3; W[i] = 10; V[i] = 8} **->** 价值高但重量也大。
- 算法将选择包裹1,总价值为20,而问题的最优解是(包裹2,包裹3),总价值为24。
贪心二号的思路
有了第二个思路,贪心二号的步骤如下
- 按重量非递减顺序排序。
- 依次考虑排序后的包裹,如果背包的剩余容量足够容纳该包裹(即放入背包的包裹总重量加上考虑的包裹重量不超过背包容量),则将考虑的包裹放入背包。
然而,这种贪心算法并非总是能给出最优解。这里有一个反例
- 问题参数:n = 3;M = 11。
- 包裹:{i = 1; W[i] = 5; V[i] = 10}; {i = 2; W[i] = 6; V[i] = 16}; {i = 3; W[i] = 10; V[i] = 28} **->** 重量轻但价值也很轻。
- 算法将选择(包裹1,包裹2),总价值为26,而问题的最优解是(包裹3),总价值为28。
贪心三号的思路
有了第三个思路,贪心三号的步骤如下。事实上,这是最广泛使用的算法。
- 按照单位成本值非递增的顺序对包裹进行排序
。你有
- 依次考虑排序后的包裹,如果背包的剩余容量足够容纳该包裹(即放入背包的包裹总重量加上考虑的包裹重量不超过背包容量),则将考虑的包裹放入背包。
**思路**:该问题的贪心思路是计算每个 的比例
。然后按比例降序排序。你将选择最高的
包裹,并且背包的容量可以容纳该包裹(剩余 > wi)。每次将一个包裹放入背包时,它也会减少背包的容量。
选择包裹的方式
- 考虑单位成本数组。你根据单位成本的递减顺序选择包裹。
- 假设你找到了一个部分解决方案:(x1, …, xi)。
- 背包的价值已获得
- 对应于已放入背包的包裹的重量
- 因此,背包剩余的重量限制是
算法步骤
你看到这是一个寻找最大值的问题。包裹列表按单位成本的降序排序以进行分支考虑。
- **步骤1**:根节点代表背包的初始状态,即你还没有选择任何包裹。
- 总价值 = 0。
- 根节点的上限 UpperBound = M * 最大单位成本。
- **步骤2**:根节点将具有子节点,对应于选择具有最高单位成本的包裹的能力。对于每个节点,重新计算参数
- 总价值 = 总价值(旧)+ 所选包裹数量 * 每个包裹的价值。
- M = M(旧)– 所选包裹数量 * 每个包裹的重量。
- UpperBound = 总价值 + M(新)* 下一个要考虑的包裹的单位成本。
- **步骤3**:在子节点中,优先处理具有较大上限的节点。此节点的子节点对应于选择下一个具有高单位成本的包裹的能力。对于每个节点,必须根据步骤2中提到的公式重新计算参数总价值、M、上限。
- **步骤4**:用以下说明重复步骤3:对于上限值小于或等于已找到的选项的临时最大成本的节点,无需再为该节点进行分支。
- **步骤5**:如果所有节点都已分支或被剪枝,则寻找最昂贵的选项。
算法的伪代码
Fractional Knapsack (Array W, Array V, int M) 1. for i <- 1 to size (V) 2. calculate cost[i] <- V[i] / W[i] 3. Sort-Descending (cost) 4. i ← 1 5. while (i <= size(V)) 6. if W[i] <= M 7. M ← M – W[i] 8. total ← total + V[i]; 9. if W[i] > M 10. i ← i+1
算法的复杂度
- 如果使用简单的排序算法(选择、冒泡…),则整个问题的复杂度为 O(n2)。
- 如果使用快速排序或归并排序,则整个问题的复杂度为 O(nlogn)。
贪心三号的Java代码
- 首先,定义类 KnapsackPackage。该类具有以下属性:重量、价值以及每个包裹的相应成本。该类的成本属性用于主算法中的排序任务。每个成本的值是
每个包裹的比例。
public class KnapsackPackage {
private double weight;
private double value;
private Double cost;
public KnapsackPackage(double weight, double value) {
super();
this.weight = weight;
this.value = value;
this.cost = new Double(value / weight);
}
public double getWeight() {
return weight;
}
public double getValue() {
return value;
}
public Double getCost() {
return cost;
}
}
- 然后创建一个函数来执行算法贪心三号。
public void knapsackGreProc(int W[], int V[], int M, int n) {
KnapsackPackage[] packs = new KnapsackPackage[n];
for (int i = 0; i < n; i ++) {
packs[i] = new KnapsackPackage(W[i], V[i]);
}
Arrays.sort(packs, new Comparator<KnapsackPackage>() {
@Override
public int compare(KnapsackPackage kPackA, KnapsackPackage kPackB) {
return kPackB.getCost().compareTo(kPackA.getCost());
}
});
int remain = M;
double result = 0d;
int i = 0;
boolean stopProc = false;
while (!stopProc) {
if (packs[i].getWeight() <= remain) {
remain -= packs[i].getWeight();
result += packs[i].getValue();
System.out.println("Pack " + i + " - Weight " + packs[i].getWeight() + " - Value " + packs[i].getValue());
}
if (packs[i].getWeight() > remain) {
i ++;
}
if (i == n) {
stopProc = true;
}
}
System.out.println("Max Value:\t" + result);
}
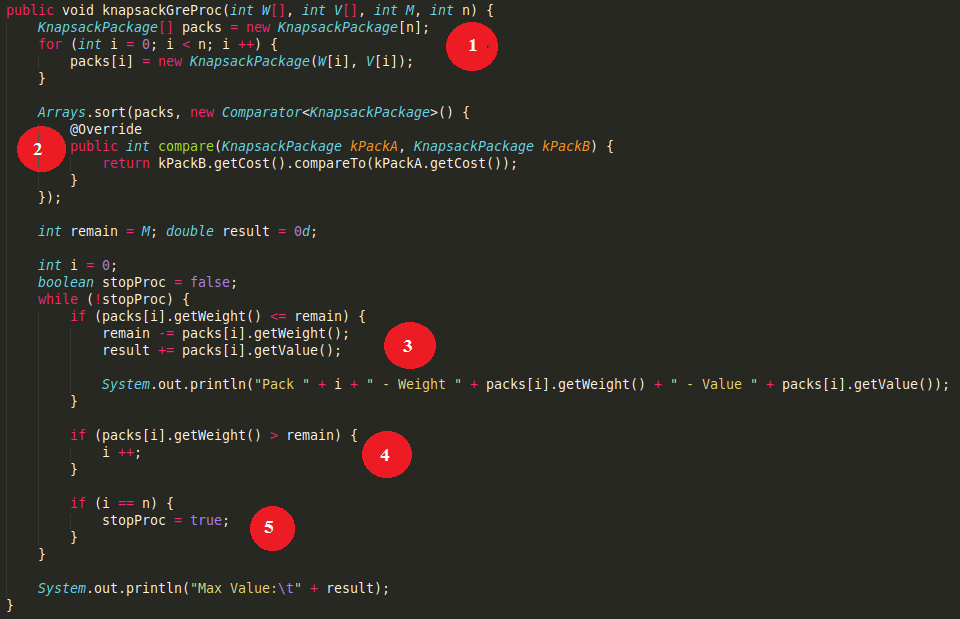
代码解释
- 为每个背包包裹初始化重量和价值。
- 按成本降序对背包包裹进行排序。
- 如果选择包裹i。
- 如果选择的包裹i数量足够。
- 浏览所有包裹时停止。
在本教程中,您有两个示例。这是使用两个示例运行上述程序的 Java 代码
public void run() {
/*
* Pack and Weight - Value
*/
//int W[] = new int[]{15, 10, 2, 4};
int W[] = new int[]{12, 2, 1, 1, 4};
//int V[] = new int[]{30, 25, 2, 6};
int V[] = new int[]{4, 2, 1, 2, 10};
/*
* Max Weight
*/
//int M = 37;
int M = 15;
int n = V.length;
/*
* Run the algorithm
*/
knapsackGreProc(W, V, M, n);
}
输出结果
- 第一个例子
Pack 0 - Weight 10.0 - Value 25.0 Pack 0 - Weight 10.0 - Value 25.0 Pack 0 - Weight 10.0 - Value 25.0 Pack 2 - Weight 4.0 - Value 6.0 Pack 3 - Weight 2.0 - Value 2.0 Max Value: 83.0
- 第二个示例
Pack 0 - Weight 4.0 - Value 10.0 Pack 0 - Weight 4.0 - Value 10.0 Pack 0 - Weight 4.0 - Value 10.0 Pack 1 - Weight 1.0 - Value 2.0 Pack 1 - Weight 1.0 - Value 2.0 Pack 1 - Weight 1.0 - Value 2.0 Max Value: 36.0
分析第一个示例
- 问题参数:n = 4;M = 37。
- 包裹:{i = 1; W[i] = 15; V[i] = 30; Cost = 2.0}; {i = 2; W[i] = 10; V[i] = 25; Cost = 2.5}; {i = 3; W[i] = 2; V[i] = 4; Cost = 1.0}; {i = 4; W[i] = 4; V[i] = 6; Cost = 1.5}。
- 按照单位成本值非递增的顺序对包裹进行排序。您有:{i = 2} **->** {i = 1} **->** {i = 4} **->** {i = 3}。
应用第一个示例算法的步骤
- 定义x1、x2、x3、x4为每个选定包裹的数量,分别对应包裹{i = 2} **->** {i = 1} **->** {i = 4} **->** {i = 3}。
- 节点根 N 代表未选择任何包裹的状态。然后
- 总价值 = 0。
- M = 37(如建议)。
- UpperBound = 37 * 2.5 = 92.5,其中37是M,2.5是包裹{i = 2}的单位成本。
- 对于包裹{i = 2},您有4种可能性:选择3个包裹{i = 2}(x1 = 3);选择2个包裹{i = 2}(x1 = 2);选择1个包裹{i = 2}(x1 = 1)和不选择包裹{i = 2}(x1 = 0)。根据这4种可能性,将根节点N分支到4个子节点N[1]、N[2]、N[3]和N[4]。
- 对于子节点N1,您有
- 总价值 = 0 + 3 * 25 = 75,其中3是选定的包裹{i = 2}的数量,25是每个包裹{i = 2}的价值。
- M = 37 – 3 * 10 = 7,其中37是背包的初始容量,3是包裹{i = 2}的数量,10是每个包裹{i = 2}的重量。
- UpperBound = 75 + 7 * 2 = 89,其中75是总价值,7是背包的剩余重量,2是包裹{i = 1}的单位成本。
- 类似地,您可以计算节点N[2]、N[3]和N[4]的参数,其中上限分别为84、79和74。
- 在节点N[1]、N[2]、N[3]和N[4]中,节点N[1]具有最大的上限,因此您将首先分支节点N[1],希望从这个方向获得一个好的计划。
- 从节点N[1]开始,您只有一个子节点N[1-1],对应于x2 = 0(因为背包剩余重量为7,而每个包裹{i = 1}的重量为15)。确定N[1-1]按钮的参数后,您发现N[1-1]的上限为85.5。
- 您继续分支节点N[1-1]。节点N[1-1]有两个子节点N[1-1-1]和N[1-1-2],分别对应于x3 = 1和x3 = 0。在确定了这两个节点的参数后,您看到N[1-1-1]的上限是84,而N[1-1-2]的上限是82,因此您继续分支节点N[1-1-1]。
- 节点N[1-1-1]有两个子节点N[1-1-1-1]和N[1-1-1-2],分别对应于x4 = 1和x4 = 0。这些是两个叶节点(代表选项),因为对于每个节点,已选择的包裹数量。其中节点N[1-1-1-1]代表选项x1 = 3,x2 = 0,x3 = 1和x4 = 1,值为83,而节点N[1-1-1-2]代表选项x1 = 3,x2 = 0,x3 = 1和x4 = 01,值为81。因此,这里的临时最大值为83。
- 回到节点N[1-1-2],您发现N[1-1-2]的上限为82 < 83,因此您修剪节点N[1-1-2]。
- 回到节点N2,您发现N2的上限为84 > 83,因此您继续分支节点N2。节点N2有两个子节点N[2-1]和N[2-2],分别对应于x2 = 1和x2 = 0。在计算了N[2-1]和N[2-2]的参数后,您发现N[2-1]的上限是83,而N[2-2]的上限是75.25。这两个值均不大于83,因此两个节点都被修剪。
- 最后,节点N3和N4也被修剪。
- 因此,树上的所有节点都已分支或被修剪,因此找到最有效的临时解决方案。因此,您需要选择3个包裹{i = 2}、1个包裹{i = 4}和1个包裹{i = 3},总价值为83,总重量为36。
通过对第二个示例进行相同的分析,您得到了结果:选择包裹4(3次)和包裹5(3次)。
贪心三号的Python3代码
- 首先,定义类 KnapsackPackage。
class KnapsackPackage(object):
""" Knapsack Package Data Class """
def __init__(self, weight, value):
self.weight = weight
self.value = value
self.cost = value / weight
def __lt__(self, other):
return self.cost < other.cost
- 然后创建一个函数来执行算法贪心三号。
class FractionalKnapsack(object):
def __init__(self):
def knapsackGreProc(self, W, V, M, n):
packs = []
for i in range(n):
packs.append(KnapsackPackage(W[i], V[i]))
packs.sort(reverse = True)
remain = M
result = 0
i = 0
stopProc = False
while (stopProc != True):
if (packs[i].weight <= remain):
remain -= packs[i].weight;
result += packs[i].value;
print("Pack ", i, " - Weight ", packs[i].weight, " - Value ", packs[i].value)
if (packs[i].weight > remain):
i += 1
if (i == n):
stopProc = True
print("Max Value:\t", result)
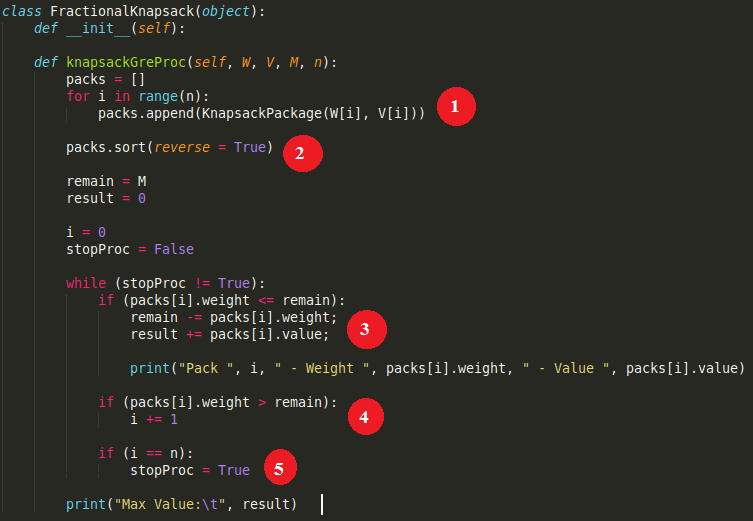
代码解释
- 为每个背包包裹初始化重量和价值。
- 按成本降序对背包包裹进行排序。
- 如果选择包裹i。
- 如果选择的包裹i数量足够。
- 浏览所有包裹时停止。
这是使用第一个示例运行上述程序的 Python3 代码
if __name__ == "__main__":
W = [15, 10, 2, 4]
V = [30, 25, 2, 6]
M = 37
n = 4
proc = FractionalKnapsack()
proc.knapsackGreProc(W, V, M, n)
输出结果
Pack 0 - Weight 10 - Value 25 Pack 0 - Weight 10 - Value 25 Pack 0 - Weight 10 - Value 25 Pack 2 - Weight 4 - Value 6 Pack 3 - Weight 2 - Value 2 Max Value: 83
贪心三号的C#代码
- 首先,定义类 KnapsackPackage。
using System;
namespace KnapsackProblem
{
public class KnapsackPackage
{
private double weight;
private double value;
private double cost;
public KnapsackPackage(double weight, double value)
{
this.weight = weight;
this.value = value;
this.cost = (double) value / weight;
}
public double Weight
{
get { return weight; }
}
public double Value
{
get { return value; }
}
public double Cost
{
get { return cost; }
}
}
}
- 然后创建一个函数来执行算法贪心三号。
using System;
namespace KnapsackProblem
{
public class FractionalKnapsack
{
public FractionalKnapsack()
{
}
public void KnapsackGreProc(int[] W, int[] V, int M, int n)
{
KnapsackPackage[] packs = new KnapsackPackage[n];
for (int k = 0; k < n; k++)
packs[k] = new KnapsackPackage(W[k], V[k]);
Array.Sort<KnapsackPackage>(packs, new Comparison<KnapsackPackage>(
(kPackA, kPackB) => kPackB.Cost.CompareTo(kPackA.Cost)));
double remain = M;
double result = 0d;
int i = 0;
bool stopProc = false;
while (!stopProc)
{
if (packs[i].Weight <= remain)
{
remain -= packs[i].Weight;
result += packs[i].Value;
Console.WriteLine("Pack " + i + " - Weight " + packs[i].Weight + " - Value " + packs[i].Value);
}
if (packs[i].Weight > remain)
{
i++;
}
if (i == n)
{
stopProc = true;
}
}
Console.WriteLine("Max Value:\t" + result);
}
}
}
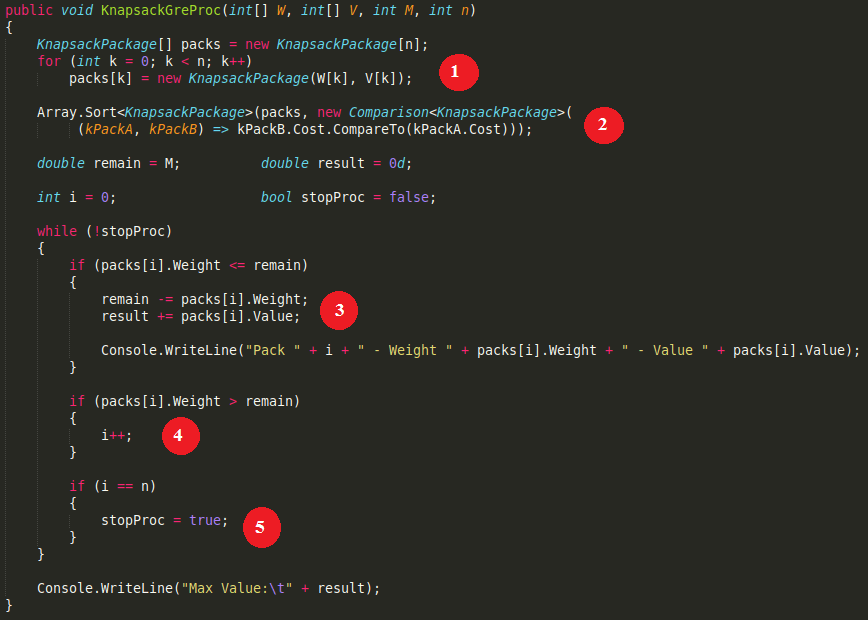
代码解释
- 为每个背包包裹初始化重量和价值。
- 按成本降序对背包包裹进行排序。
- 如果选择包裹i。
- 如果选择的包裹i数量足够。
- 浏览所有包裹时停止。
这是使用第一个示例运行上述程序的 C# 代码
public void run()
{
/*
* Pack and Weight - Value
*/
int[] W = new int[]{15, 10, 2, 4};
//int[] W = new int[] { 12, 2, 1, 1, 4 };
int[] V = new int[]{30, 25, 2, 6};
//int[] V = new int[] { 4, 2, 1, 2, 10 };
/*
* Max Weight
*/
int M = 37;
//int M = 15;
int n = V.Length;
/*
* Run the algorithm
*/
KnapsackGreProc(W, V, M, n);
}
输出结果
Pack 0 - Weight 10 - Value 25 Pack 0 - Weight 10 - Value 25 Pack 0 - Weight 10 - Value 25 Pack 2 - Weight 4 - Value 6 Pack 3 - Weight 2 - Value 2 Max Value: 83
贪心三号的反例
贪心三号的算法在某些情况下可以快速解决并且是最优的。但是,在某些特殊情况下,它不能给出最优解。这里有一个反例
- 问题参数:n = 3;M = 10。
- 包裹:{i = 1; W[i] = 7; V[i] = 9; Cost = 9/7}; {i = 2; W[i] = 6; V[i] = 6; Cost = 1}; {i = 3; W[i] = 4; V[i] = 4; Cost = 1}。
- 算法将选择(包裹1),总价值为9,而问题的最优解是(包裹2,包裹3),总价值为10。
这是使用反例运行上述程序的 Java 代码
public void run() {
/*
* Pack and Weight - Value
*/
int W[] = new int[]{7, 6, 4};
int V[] = new int[]{9, 6, 4};
/*
* Max Weight
*/
int M = 10;
int n = V.length;
/*
* Run the algorithm
*/
knapsackGreProc(W, V, M, n);
}
结果如下
Pack 0 - Weight 7.0 - Value 9.0 Max Value: 9.0
这就是分数背包问题。