BFS vs DFS – 它们之间的区别

什么是 BFS？

BFS 是一种用于图数据或搜索树或遍历结构的算法。该算法以精确的广度优先方式高效地访问和标记图中的所有关键节点。

该算法选择图中的一个节点（起始或源点），然后访问选定节点的所有邻近节点。一旦算法访问并标记了起始节点，它就会移动到最近的未访问节点并对其进行分析。

访问过的所有节点都会被标记。这些迭代将继续进行，直到图的所有节点都被成功访问并标记。BFS 的全称是广度优先搜索。

什么是 DFS？

DFS 是一种用于以深度方向查找或遍历图或树的算法。算法的执行从根节点开始，在回溯之前探索每个分支。它使用栈数据结构来记住下一个要访问的顶点，并在任何迭代中出现死胡同时启动搜索。DFS 的全称是深度优先搜索。

BFS 和 DFS 二叉树的区别

以下是 BFS 和 DFS 的重要区别。

BFS	DFS
BFS 找到到目的地的最短路径。	DFS 深入子树底部，然后回溯。
BFS 的全称是广度优先搜索。	DFS 的全称是深度优先搜索。
它使用队列来跟踪下一个要访问的位置。	它使用栈来跟踪下一个要访问的位置。
BFS 按照树的层级进行遍历。	DFS 按照树的深度进行遍历。
它使用 FIFO 列表实现。	它使用 LIFO 列表实现。
与 DFS 相比，它需要更多的内存。	与 BFS 相比，它需要的内存更少。
此算法提供最浅的路径解决方案。	此算法不保证最浅路径解决方案。
BFS 不需要回溯。	DFS 需要回溯。
您永远不会陷入有限循环。	您可能会陷入无限循环。
如果您找不到任何目标，可能需要扩展许多节点才能找到解决方案。	如果您找不到任何目标，可能会发生叶节点回溯。

BFS 示例

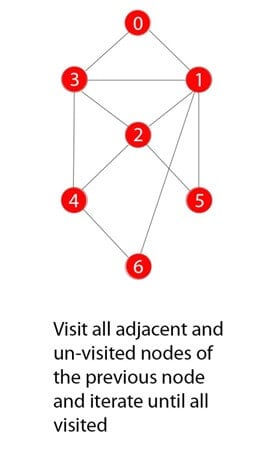
在下面的 BFS 示例中，我们使用了具有 6 个顶点的图。

BFS 示例

步骤 1)

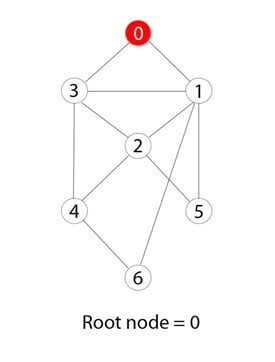
您有一个从 0 到 6 的七个数字组成的图。

步骤 2)

0 或零被标记为根节点。

步骤 3)

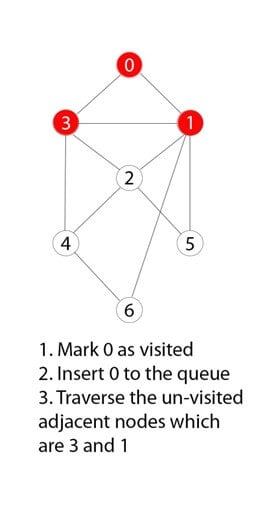
0 被访问、标记并插入队列数据结构。

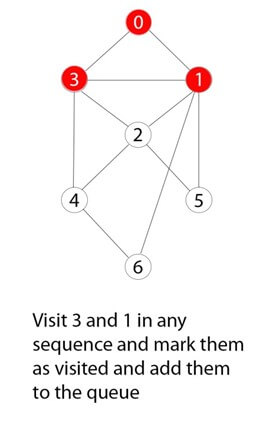
步骤 4)

0 的剩余邻近且未访问的节点被访问、标记并插入队列。

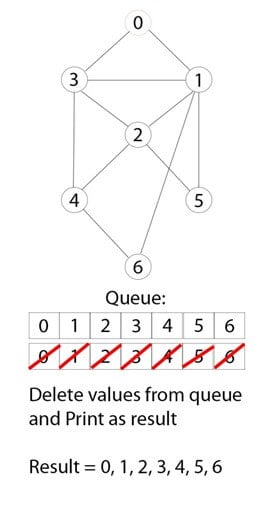
步骤 5)

遍历迭代重复进行，直到所有节点都被访问。

DFS 示例

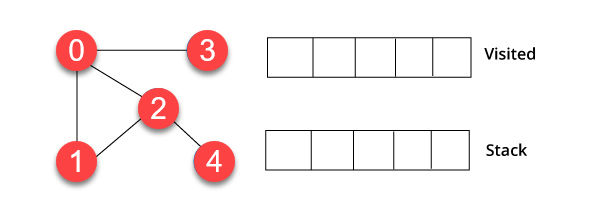
在下面的 DFS 示例中，我们使用了一个具有 5 个顶点的无向图。

步骤 1)

我们从顶点 0 开始。算法开始时，将其放入访问列表，同时将其所有邻近顶点放入一个称为栈的数据结构中。

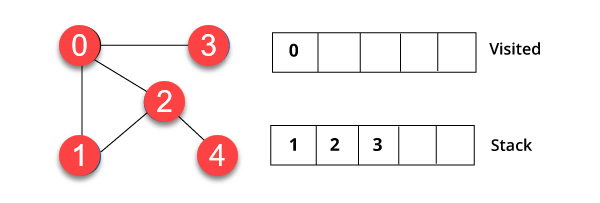
步骤 2)

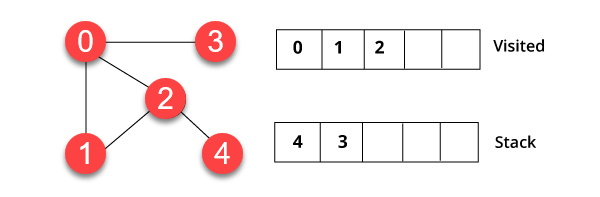
您将访问栈顶的元素，例如 1，然后转到其邻近节点。这是因为 0 已经被访问过了。因此，我们访问顶点 2。

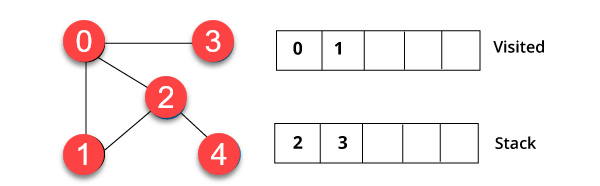
步骤 3)

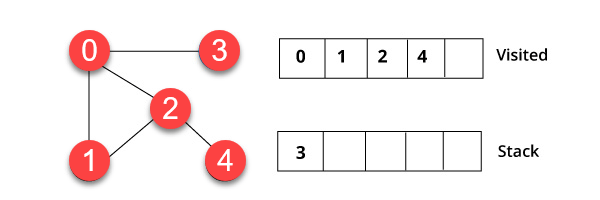
顶点 2 有一个未访问的邻近顶点 4。因此，我们将其添加到栈中并访问它。

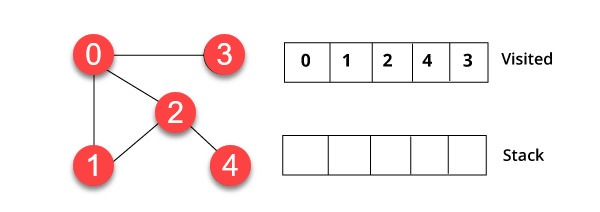
步骤 4)

最后，我们将访问最后一个顶点 3，它没有任何未访问的邻近节点。我们已经使用 DFS 算法完成了图的遍历。

BFS 的应用

以下是 BFS 的应用

无权图

BFS 算法可以轻松创建最短路径和最小生成树，以最短的时间以高精度访问图的所有顶点。

P2P 网络

BFS 可用于在点对点网络中定位所有最近或邻近的节点。这将更快地找到所需数据。

网络爬虫

搜索引擎或网络爬虫可以通过采用 BFS 来轻松构建多个级别的索引。BFS 实现从源（网页）开始，然后访问该源的所有链接。

网络广播

BFS 算法通过广播数据包来查找和到达它所寻址的所有节点。

DFS 的应用

以下是 DFS 的重要应用

加权图

在加权图中，DFS 图遍历生成最短路径树和最小生成树。

检测图中的循环

如果在 DFS 期间找到反向边，则图具有循环。因此，我们应该对图运行 DFS 并验证反向边。

路径查找

我们可以专门化 DFS 算法来搜索两个顶点之间的路径。

拓扑排序

它主要用于调度作业，从给定的依赖关系中进行安排。在计算机科学中，它用于指令调度、数据序列化、逻辑综合、确定编译任务的顺序。

搜索图的强连通分量

当图中的每个顶点与其他剩余顶点都有路径时，它在 DFS 图中使用。

解决只有一种解决方案的谜题

通过将路径上的节点包含在访问集合中，可以轻松地将 DFS 算法改编为搜索迷宫的所有解决方案。