选择排序:Python 代码示例说明算法
什么是选择排序?
选择排序是一种比较排序算法,用于将随机项目列表按升序排序。比较不需要很多额外的空间。它只需要一个额外的内存空间用于临时变量。
这被称为原地排序。选择排序的时间复杂度为 O(n2),其中 n 是列表中项目的总数。时间复杂度衡量排序列表所需的迭代次数。列表被分成两个部分:第一个列表包含已排序的项目,而第二个列表包含未排序的项目。
默认情况下,已排序列表为空,未排序列表包含所有元素。然后扫描未排序列表以查找最小值,然后将其放入已排序列表中。此过程重复进行,直到所有值都已比较并排序。
选择排序如何工作?
未排序分区中的第一个项目将与右侧的所有值进行比较,以检查它是否是最小值。如果不是最小值,则将其位置与最小值交换。如果最小值的索引是 3,则将索引为 3 的元素的值放在索引 0 处,而索引 0 处的值放在索引 3 处。如果未排序分区中的第一个元素是最小值,则返回其位置。
示例
- 例如,如果最小值的索引为 3,则将索引为 3 的元素的值放在索引 0 处,而索引 0 处的值放在索引 3 处。如果未排序分区中的第一个元素是最小值,则返回其位置。
- 然后将已被确定为最小值的元素移到左侧分区,即已排序列表。
- 分区侧现在有一个元素,而未分区侧有 (n – 1) 个元素,其中 n 是列表中的元素总数。此过程一遍又一遍地重复,直到所有项目都已根据其值进行比较和排序。
问题定义
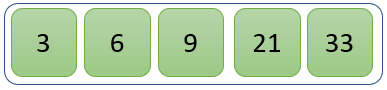
需要将一列无序的元素按升序排序。以下列表为例。
[21,6,9,33,3]
上面的列表应排序以产生以下结果
[3,6,9,21,33]
解决方案(算法)
步骤 1) 获取 n 的值,即数组的总大小
步骤 2) 将列表划分为已排序和未排序的部分。已排序部分最初为空,而未排序部分包含整个列表
步骤 3) 从未排序部分中选择最小值并将其放入已排序部分。
步骤 4) 重复此过程 (n – 1) 次,直到列表中的所有元素都已排序。
可视化表示
给定一个包含五个元素的列表,下图说明了选择排序算法在排序它们时如何迭代值。
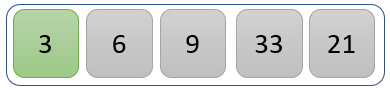
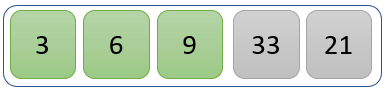
下图显示了未排序列表
步骤 1)
第一个值 21 与其余值进行比较,以检查它是否是最小值。
3 是最小值,因此交换 21 和 3 的位置。带有绿色背景的值表示列表的已排序部分。
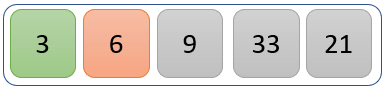
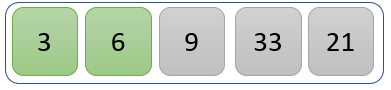
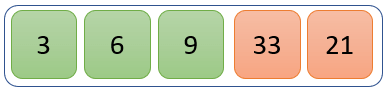
步骤 2)
未排序分区中的第一个值 6 与其余值进行比较,以找出是否存在更小的值
值 6 是最小值,因此它保持其位置。
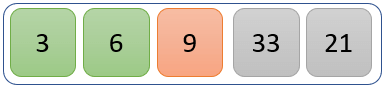
步骤 3)
未排序列表的第一个元素 9 将与其余值进行比较,以检查它是否是最小值。
值 9 是最小值,因此它在已排序分区中保持其位置。
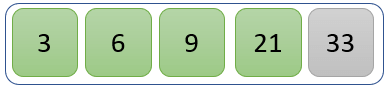
步骤 4)
值 33 与其余值进行比较。
值 21 小于 33,因此交换位置以生成上述新列表。
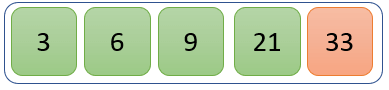
步骤 5)
未分区列表中只剩一个值。因此,它已经被排序。
最终列表与上图所示类似。
使用 Python 3 的选择排序程序
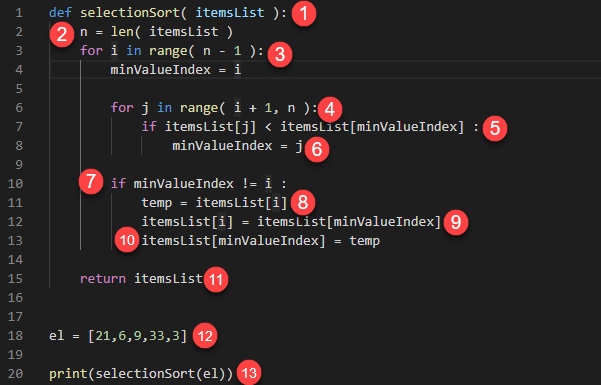
以下代码显示了使用 Python 3 的选择排序实现
def selectionSort( itemsList ):
n = len( itemsList )
for i in range( n - 1 ):
minValueIndex = i
for j in range( i + 1, n ):
if itemsList[j] < itemsList[minValueIndex] :
minValueIndex = j
if minValueIndex != i :
temp = itemsList[i]
itemsList[i] = itemsList[minValueIndex]
itemsList[minValueIndex] = temp
return itemsList
el = [21,6,9,33,3]
print(selectionSort(el))
运行上述代码会产生以下结果
[3, 6, 9, 21, 33]
代码解释
代码解释如下
代码解释
- 定义一个名为 selectionSort 的函数
- 获取列表中元素的总数。我们需要此来确定比较值时要进行的传递次数。
- 外循环。使用循环迭代列表中的值。迭代次数为 (n – 1)。n 的值为 5,因此 (5 – 1) 为 4。这意味着外层迭代将执行 4 次。在每次迭代中,变量 i 的值被赋给变量 minValueIndex
- 内循环。使用循环将最左边的值与右侧的其他值进行比较。但是,j 的值不从索引 0 开始。它从 (i + 1) 开始。这排除了已排序的值,以便我们专注于尚未排序的项目。
- 查找未排序列表中的最小值并将其放置在其正确位置
- 当交换条件为真时更新 minValueIndex 的值
- 比较 minValueIndex 和 i 的索引号的值,看它们是否不相等
- 最左边的值存储在临时变量中
- 右侧的较小值首先占据位置
- 存储在临时值中的值存储在之前由最小值占据的位置
- 将排序后的列表作为函数结果返回
- 创建一个名为 el 的列表,其中包含随机数
- 在调用 selection Sort 函数并将 el 作为参数传递后,打印排序后的列表。
选择排序的时间复杂度
排序复杂度用于表示排序列表所需的执行次数。实现有两个循环。
逐个选择列表值的外部循环执行 n 次,其中 n 是列表中值的总数。
内部循环将外部循环的值与其余值进行比较,也执行 n 次,其中 n 是列表中元素的总数。
因此,执行次数为 (n * n),也可以表示为 O(n2)。
选择排序有三个复杂度类别:
- 最坏情况 - 这发生在提供的列表是降序排列的情况下。算法执行的最大执行次数为 [Big-O] O(n2)
- 最佳情况 - 这发生在提供的列表已排序时。算法执行的最少执行次数为 [Big-Omega] ?(n2)
- 平均情况 - 这发生在列表是随机顺序的情况下。平均复杂度表示为 [Big-theta] ?(n2)
选择排序的空间复杂度为 O(1),因为它只需要一个用于交换值的临时变量。
何时使用选择排序?
当您想这样做时,最好使用选择排序
- 您必须将一小部分项目按升序排序
- 当交换值的成本可以忽略不计时
- 它还用于需要确保列表中所有值都已被检查的情况。
选择排序的优点
以下是选择排序的优点
- 它在小型列表中表现出色
- 它是一种原地算法。它不需要太多空间即可排序。只需要一个额外的空间来保存临时变量。
- 它在已排序的项目上表现良好。
选择排序的缺点
以下是选择排序的缺点。
- 在处理大型列表时,它的表现很差。
- 排序期间的迭代次数为 n 的平方,其中 n 是列表中元素的总数。
- 与其他算法相比,例如快速排序,其性能更优。
摘要
- 选择排序是一种原地比较算法,用于将随机列表排序为有序列表。其时间复杂度为 O(n2)
- 列表被分成两部分:已排序和未排序。从未排序部分中选择最小值并放入已排序部分。
- 此过程重复进行,直到所有项目都已排序。
- 使用 Python 3 实现伪代码涉及使用两个 for 循环和 if 语句来检查是否需要交换
- 时间复杂度衡量排序列表所需的步骤数。
- 最坏情况时间复杂度发生在列表降序排列时。其时间复杂度为 [Big-O] O(n2)
- 最佳情况时间复杂度发生在列表已按升序排列时。其时间复杂度为 [Big-Omega] ?(n2)
- 平均情况时间复杂度发生在列表是随机顺序时。其时间复杂度为 [Big-theta] ?(n2)
- 当您有少量项目要排序、交换值的成本无关紧要以及必须检查所有值时,选择排序是最佳选择。
- 选择排序在处理大型列表时表现不佳
- 与其他排序算法(如快速排序)相比,选择排序的性能较差。