堆排序算法(附Python和C++代码)
什么是堆排序算法?
堆排序是最流行且最快的排序算法之一。它基于完全二叉树数据结构。我们将寻找最大元素并将其放在最大堆的顶部。我们将将其放置在二叉树的父节点上。
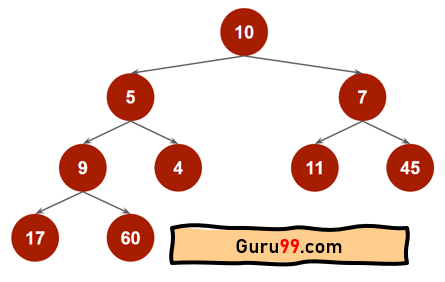
假设给出一个数组,data = [10,5, 7, 9, 4, 11, 45, 17, 60]。
在数组中,如果 i 索引(i=0,1,2,3 …)是父节点,那么 (2i+1) 和 (2i+2) 将是左子节点和右子节点。用这个数组创建一个完全二叉树会像这样
我们将从数组的开头到结尾进行堆化过程。最初,如果我们把数组转换成一棵树,它看起来就像上面那样。我们可以看到它没有维护任何堆属性(最小堆或最大堆)。通过对所有节点进行堆化过程,我们将获得排序后的数组。
堆排序的应用
以下是堆排序算法的一些用法
- 构建“优先队列”需要堆排序。因为堆排序在每次插入后都会保持元素有序。
- 堆数据结构在查找给定数组中第 k 个最大元素方面非常高效。
- Linux 内核将堆排序用作默认的排序算法,因为它具有 O(1) 的空间复杂度。
创建堆排序及示例
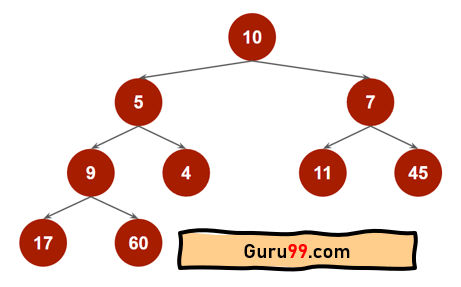
在这里,我们将从以下完全二叉树构建一个最大堆。
叶子节点是 17、60、4、11 和 45。它们没有任何子节点。这就是为什么它们是叶子节点。因此,我们将从它们的父节点开始堆化方法。以下是步骤
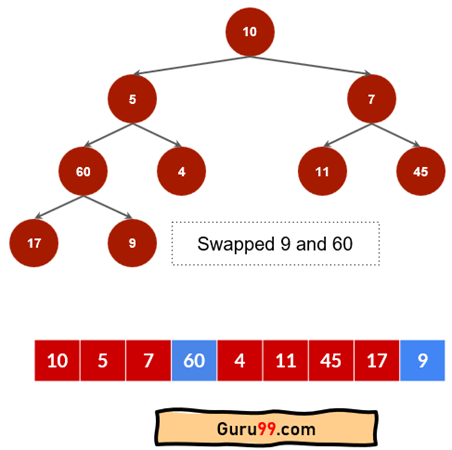
步骤 1) 选择最左边的子树。如果子节点更大,则将父节点与子节点交换。
这里的父节点是 9。子节点是 17 和 60。因为 60 是最大的,所以 60 和 9 将被交换以维护最大堆。
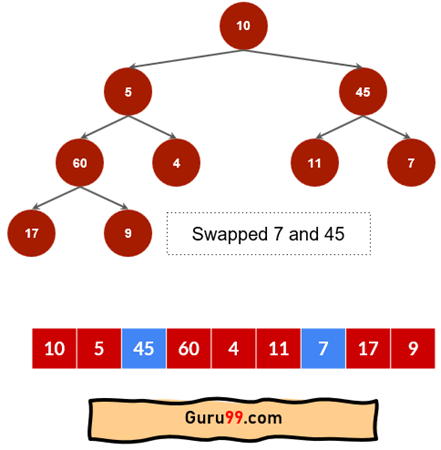
步骤 2) 现在,最左边的子树已堆化。下一个父节点是 7。这个父节点有两个子节点,最大的节点是 45。因此,45 和 7 将被交换。
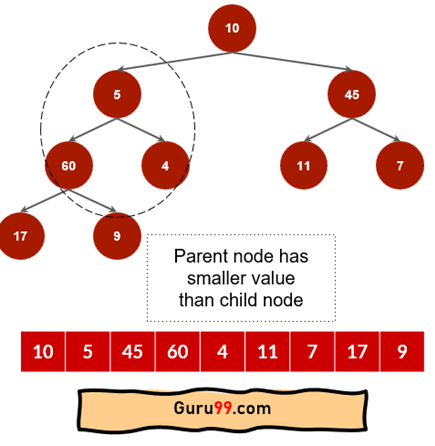
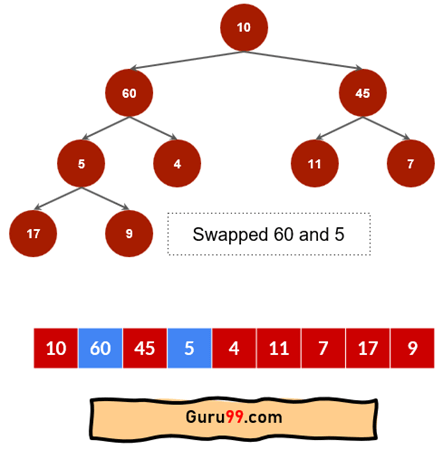
步骤 3) 节点 60 和 4 的父节点是 5。因为“5”小于子节点 60,所以它将被交换。
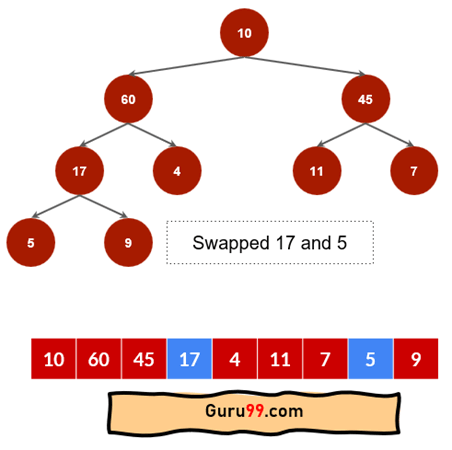
步骤 4) 现在,节点 5 有子节点 17,9。这不符合最大堆属性。所以,5 将被 17 替换。
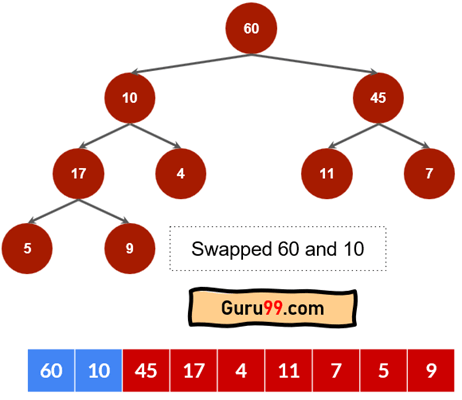
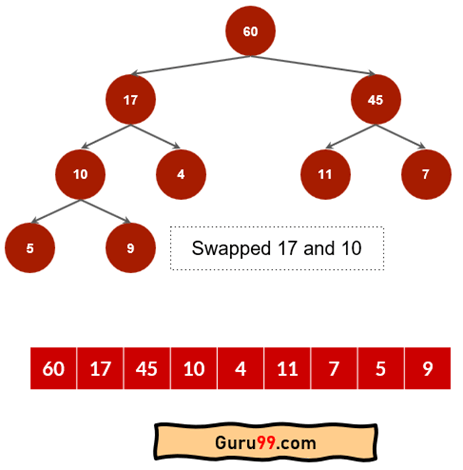
步骤 5) 节点 10 将与 60 交换,然后与 17 交换。过程将如下所示。
步骤 6) 到步骤 5 为止,我们创建了最大堆。每个父节点都比其子节点大。根节点具有最大值(60)。
注意:要创建排序后的数组,我们需要将最大值节点替换为其后继节点。
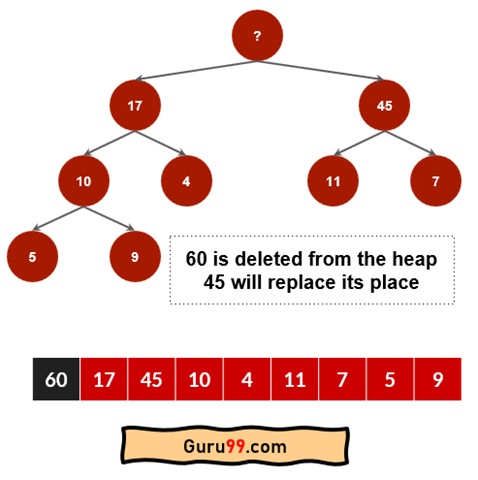
这个过程称为“提取最大值”。因为 60 是最大节点,我们将把它的位置固定在第 0 个索引,并创建一个不包含节点 60 的堆。
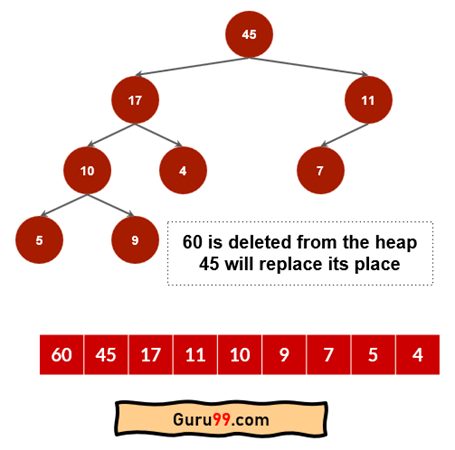
步骤 7) 由于 60 被移除,下一个最大值是 45。我们将从节点 45 再次执行“提取最大值”过程。
这次我们将得到 45 并用其后继节点 17 替换根节点。
我们需要执行“提取最大值”直到所有元素都被排序。
执行这些步骤直到提取所有最大值后,我们将得到以下数组。
什么是二叉堆?
二叉堆是一种完全二叉树数据结构。在这种树结构中,父节点要么小于子节点,要么大于子节点。如果父节点较小,则堆称为“最小堆”;如果父节点较大,则堆称为“最大堆”。
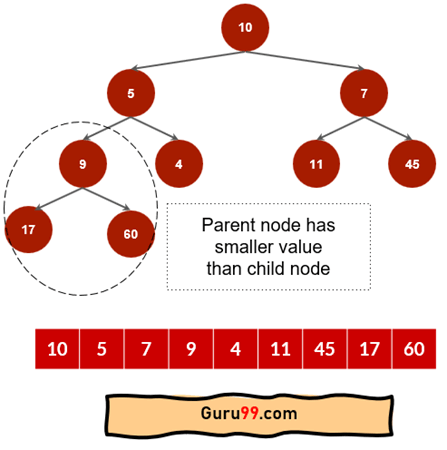
以下是最小堆和最大堆的示例。
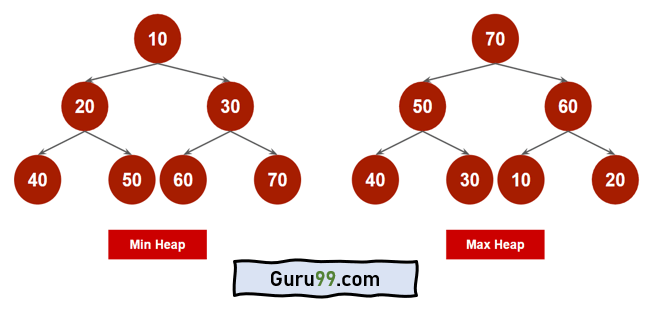
在上图中,如果您注意到“最小堆”,父节点总是小于其子节点。在树的顶部,我们可以找到最小值 10。
同样,对于“最大堆”,父节点总是大于子节点。最大元素存在于“最大堆”的根节点。
什么是“堆化”?
“堆化”是堆的原则,它确保了节点的位置。在堆化中,最大堆始终保持父子关系,即父节点大于子节点。
例如,如果添加了一个新节点,我们需要重新调整堆的形状。但是,我们可能需要更改或交换节点或重新排列数组。这个重新调整堆的过程称为“堆化”。
以下是一个堆化工作原理的示例
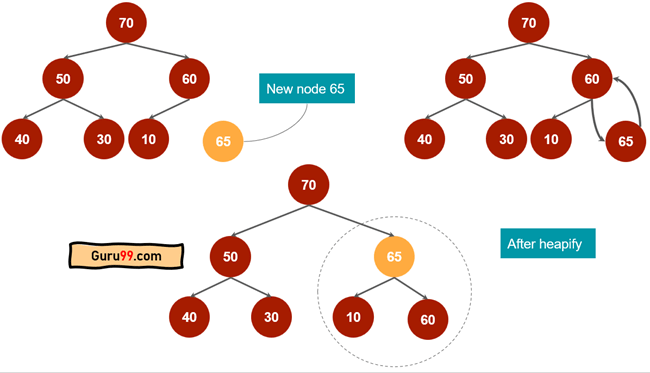
以下是堆化的步骤
步骤 1) 将节点 65 添加为节点 60 的右子节点。
步骤 2) 检查新添加的节点是否大于其父节点。
步骤 3) 因为它大于父节点,所以我们将右子节点与其父节点交换。
如何构建堆
在构建堆或堆化树之前,我们需要知道如何存储它。由于堆是完全二叉树,因此最好使用数组来存储堆的数据。
假设一个数组总共包含 n 个元素。如果“i”索引是父节点,那么左子节点将在索引 **(2i+1)**,右子节点将在索引 **(2i+2)**。我们假设数组索引从 0 开始。
使用此,让我们将最大堆存储到类似下面的数组中
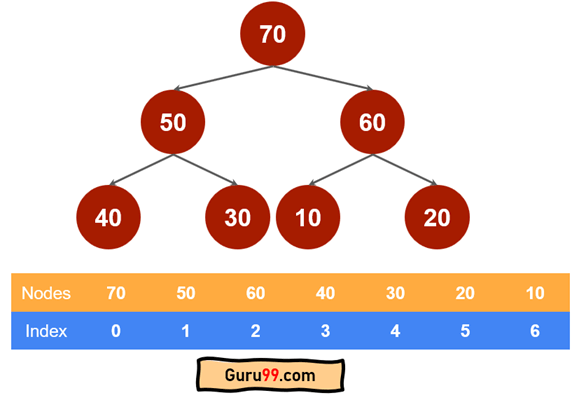
堆化算法维护堆属性。如果父节点不具有极端值(最小或最大),它将被与最极端的子节点交换。
以下是堆化最大堆的步骤
步骤 1) 从叶子节点开始。
步骤 2) 找到父节点和子节点之间的最大值。
步骤 3) 如果子节点的值大于父节点,则交换节点。
步骤 4) 向上移动一级。
步骤 5) 重复步骤 2、3、4,直到到达索引 0 或排序整个树。
以下是递归堆化的伪代码(最大堆)
def heapify(): input→ array, size, i largest = i left = 2*i + 1 right = 2*i + 2 if left<n and array[largest ] < array[left]: largest = left if right<n and array[largest ] < array[right]: largest = right If largest not equals i: swap(array[i],array[largest]) heapify(array,n,largest)
堆排序伪代码
以下是堆排序算法的伪代码
Heapify(numbers as an array, n as integer, i as integer): largest = i left = 2i+1 right= 2i+2 if(left<=n) and (numbers[i]<numbers[left]) largest=left if(right<=n) and (numbers[i]<numbers[right]) largest=right if(largest != i) swap(numbers[i], numbers[largest]) Heapify(numbers,n,largest) HeapSort(numbers as an array): n= numbers.size() for i in range n/2 to 1 Heapify(numbers,n,i) for i in range n to 2 Swap numbers[i] with numbers[1] Heapify(numbers,i,0)
C++ 堆排序代码示例
#include <iostream>
using namespace std;
void display(int arr[], int n)
{
for (int i = 0; i < n; i++)
{
cout << arr[i] << "\t";
}
cout << endl;
}
void heapify(int numbers[], int n, int i)
{
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < n && numbers[left] < numbers[largest])
{
largest = left;
}
if (right < n && numbers[right] < numbers[largest])
{
largest = right;
}
if (largest != i)
{
//uncomment the following line to see details in output
//cout<<"Swapping "<< numbers[i]<< " and "<<numbers[largest]<<endl;
swap(numbers[i], numbers[largest]);
heapify(numbers, n, largest);
}
}
void heapSort(int numbers[], int n)
{
for (int i = n/2 - 1; i >= 0; i--)
{
heapify(numbers, n, i);
//uncomment the following line to see details in output
//cout<<"Heapify:\t";
//display(numbers,n);
}
for (int i = n - 1; i >= 0; i--)
{
swap(numbers[0], numbers[i]);
heapify(numbers, i, 0);
}
}
int main()
{
int numbers[] = { 10,5, 7, 9, 4, 11, 45, 17, 60};
int size = sizeof(numbers) / sizeof(numbers[0]);
cout<<"Initial Array:\t";
display(numbers,size);
heapSort(numbers, size);
cout<<"Sorted Array (descending order):\t";
display(numbers, size);
}
输出
Initial Array: 10 5 7 9 4 11 45 17 60 Sorted Array (descending order): 60 45 17 11 10 9 7 5 4
Python 堆排序代码示例
def display(arr):
for i in range(len(arr)):
print(arr[i], end = "\t")
print()
def heapify(numbers, n, i):
largest = i
left = 2 * i + 1
right = 2 * i + 2
if left < n and numbers[left] < numbers[largest]:
largest = left
if right < n and numbers[right] < numbers[largest]:
largest = right
if largest != i:
numbers[i], numbers[largest] = numbers[largest], numbers[i]
heapify(numbers, n, largest)
def heapSort(items, n):
for i in range(n //2,-1,-1):
heapify(items, n, i) for i in range(n - 1, -1, -1):
items[0], items[i] = items[i], items[0] heapify(items, i, 0) numbers = [10, 5, 7, 9, 4, 11, 45, 17, 60] print("Initial List:\t", end = "") display(numbers) print("After HeapSort:\t", end = "") heapSort(numbers, len(numbers)) display(numbers)
输出
Initial List: 10 5 7 9 4 11 45 17 60 After HeapSort: 60 45 17 11 10 9 7 5 4
堆排序的时间和空间复杂度分析
对于堆排序,我们可以分析时间复杂度和空间复杂度。对于时间复杂度,我们有以下情况
- 最佳情况
- 平均情况
- 最坏情况
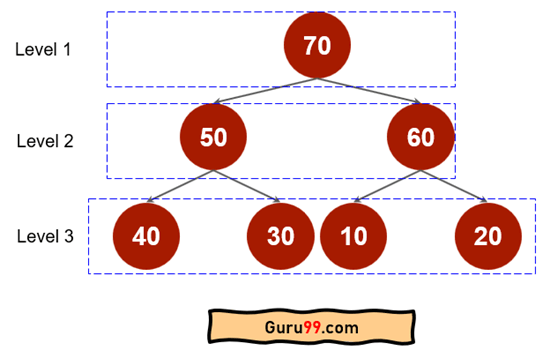
堆是在完全二叉树上实现的。因此,在二叉树的底层将有最多的节点。如果底层有 n 个节点,则上一层将有 n/2 个节点。
在这个例子中,第 3 层有四个项目,第 2 层有两个项目,第 1 层有一个项目。如果总共有 n 个项目,则高度或总层数将是 **Log2(n)**。因此,插入单个元素最多可能需要 Log(n) 次迭代。
当我们想从堆中获取最大值时,只需获取根节点。然后再次运行堆化。每次堆化需要 **Log2(n)** 时间。提取最大值需要 O(1) 时间。
堆排序算法的最佳情况时间复杂度
当数组中的所有元素都已排序时,构建堆需要 O(n) 时间。因为如果列表已排序,则插入一个项将花费常量时间 O(1)。
因此,在最佳情况下,创建最大堆或最小堆需要 O(n) 时间。
堆排序算法的平均情况时间复杂度
插入一个项或提取最大值需要 O(log(n)) 时间。因此,堆排序算法的平均情况时间复杂度为 **O(n log(n))**。
堆排序算法的最坏情况时间复杂度
与平均情况类似,在最坏的情况下,我们可能需要执行 n 次堆化。每次堆化需要 O(log(n)) 时间。因此,最坏情况时间复杂度为 **O(n log(n))**。
堆排序算法的空间复杂度
堆排序是一种原地设计算法。这意味着执行任务不需要额外的或临时的内存。如果我们查看实现,我们会注意到我们使用了 swap() 来执行节点交换。没有需要其他的列表或数组。因此,空间复杂度为 O(1)。