最长公共子序列：Python、C++ 示例

什么是最长公共子序列？

最长公共子序列（LCS）是指给出两个字符串/模式/对象序列。在这两个序列/字符串中，您需要找到在两个字符串或模式中以相同顺序存在的元素的最长子序列。

示例

例如，提供了两个字符串。

我们假设：

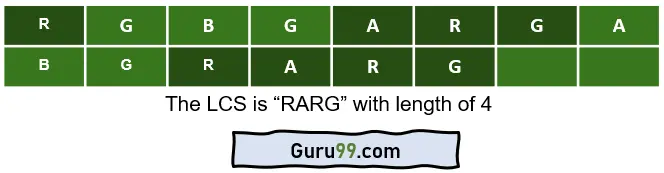
模式_1 = “RGBGARGA”
模式_2 = “BGRARG”

从模式_1，可以产生序列，例如“RGB”、“RGGA”、“RGAR”。要创建序列，您需要维护字符串中每个字符的相对位置。
从模式_2，我们可以产生序列，例如“BGR”、“BRAG”、“RARG”。只要序列保持原始字符串的相对位置，就可以产生序列。

相对位置一词是指顺序。

例如，“BRG”是一个有效的序列，因为在原始字符串模式_2中，“B”先出现，然后是“R”，然后是“G”。但是，如果序列是“RBRG”，则无效。因为在原始字符串（模式_2）中，“B”先出现。

我们有两种方法可以从给定的两个序列或数组中找到最长公共子序列。

朴素方法
动态规划解决方案：最长公共子序列也称为 LCS。

朴素解决方案的时间复杂度较高，并非最优解决方案。使用动态规划解决方案（DP），我们可以解决复杂性问题。

朴素方法

朴素方法是一种解决问题的简单方法，不考虑时间复杂度和其他优化因素。

朴素方法包括“蛮力法”，多重循环，以及大多数情况下的递归方法。

蛮力法的意思是遍历给定问题的所有可能模式。

示例

根据上面模式1和模式2的例子，假设模式1的长度为m，模式2的长度为n。为了检查每种可能的情况，我们需要用模式2评估模式1的所有可能子序列。

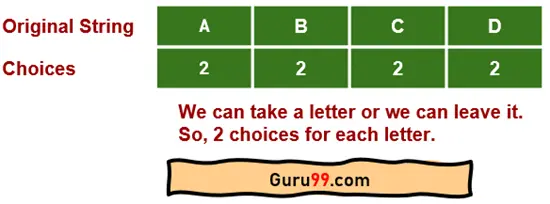
这是一个简单的四字母字符串“ABCD”。例如，我们需要从“ABCD”创建一个序列。我们可以选择一个字符，也可以不选择。这意味着，对于每个字符，我们有两个选择。

它们是

该字符将被添加到子序列中。
该字符将不会被添加到子序列中。

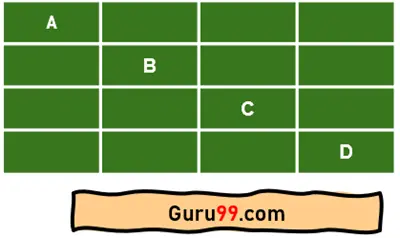
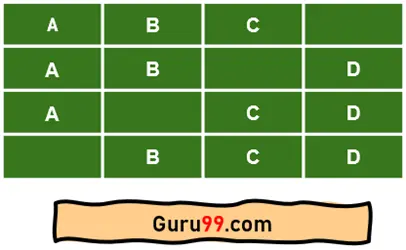
这里，图片显示了我们可以从字符串“ABCD”制作的所有序列。

单字符序列

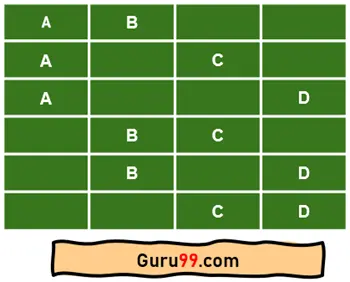
双字符序列

三字符序列

从上面的图可以看出，有14个序列。如果我们不取字母，基本上是空字符串，总序列数为15。此外，“ABCD”字符串本身就是一个序列。所以，总序列数为16。

因此，从“ABCD”可以生成 2⁴ 或 16 个子序列。那么，长度为 **m** 的字符串将总共有 2^m 个子序列。

对于每个子序列，我们需要将其与整个模式2进行比较。这需要0(n)的时间。0(n)是指计算执行时间的复杂性函数。

所以，总时间复杂度为 **O(n*2^m)。** 对于上面例子，我们看到 m=8，n=5。

以下是朴素方法的步骤

步骤 1） 从模式1中获取一个序列。
步骤 2） 将步骤1中的序列与模式2进行匹配。
步骤 3） 如果匹配，则保存该子序列。
步骤 4） 如果模式1中还有更多序列，则再次转到步骤1。
步骤 5） 打印最长的子序列。

最优子结构

最优子结构一词是指可以通过解决子问题找到最优（简单）解。例如，在上面的例子中，我们有模式1和模式2。

步骤 1） 从每个模式中取前两个字符

步骤 2） 从每个模式中取第三到第五个字符。

步骤 3） 以此类推，继续处理剩余的字符。

我们对子字符串（从原始字符串生成的字符串）查找 LCS。然后我们记录子字符串 LCS 的长度。

现在，还有另一个有趣的属性是**重叠子问题**。如果问题陈述可以分解为小程序问题并在程序中多次使用，则该问题被认为具有重叠子问题。

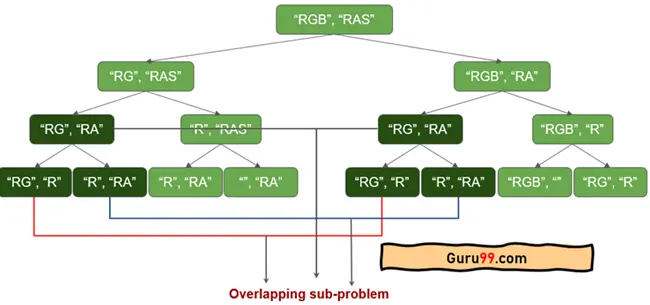
下图显示递归算法多次调用具有相同参数的函数。

例如，让我们看一下递归树。

在深色框中，您可以注意到重叠子问题。（“RG”、“RA”）、（“RG”、“R”）等被调用了多次。

为了优化这一点，我们采用了**动态规划**（DP）方法。

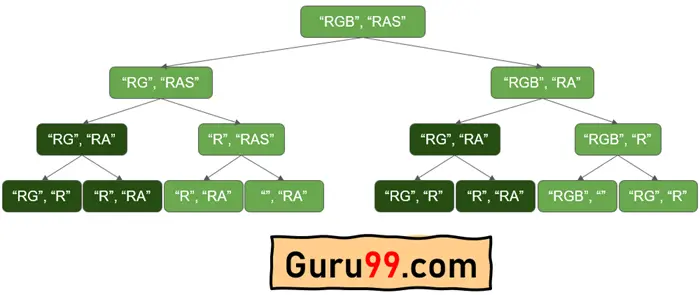
最长公共子序列的递归方法

上面显示的图是递归方法。每个递归函数都有一个基本情况来中断递归或开始从其堆栈返回。

对于这个实现，我们将使用一个基本情况。所以，**算法**如下：

如果最后一个元素之前的所有元素都匹配，则将长度加一并返回
将两个模式传递给函数，并取返回值的最大值
如果一个模式的长度为零，那么我们就没有可以比较的子序列。在这种情况下返回 0。这是递归的基本情况。

伪代码

def lcs:
    input: pattern_1, pattern_2, len_1, len_2
if len_1 or len_2 is zero:
    then
return 0
if pattern_1[len_1 - 1] equals pattern_2[len_2 - 1]
then
return 1 + lcs(pattern_1, pattern_2,
    len_1 - 1, len_2 - 1)
else
    max of lcs(pattern_1, pattern_2, len_1 - 1, len_2),
    lcs(pattern_1, pattern_2, len_1, len_2 - 1)

C++ 实现

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int lcs(string pattern_1, string pattern_2, int len_1, int len_2) {
  if (len_1 == 0 || len_2 == 0)
    return 0;
  if (pattern_1[len_1 - 1] == pattern_2[len_2 - 1]) {
    return 1 + lcs(pattern_1, pattern_2, len_1 - 1, len_2 - 1);
  } else {
    return max(lcs(pattern_1, pattern_2, len_1 - 1, len_2), lcs(pattern_1, pattern_2, len_1, len_2 - 1));
  }
}
int main() {
  string pattern_1, pattern_2;
  pattern_1 = "RGBGARGA";
  pattern_2 = "BGRARG";
  cout<<"Length of LCS is: "<<lcs(pattern_1, pattern_2, pattern_1.size(), pattern_2.size())<<endl;
}

输出

Length of LCS is: 5

Python 实现

def lcs(pattern_1, pattern_2, len_1, len_2):
    if len_1 == 0 or len_2 == 0:
    return 0
if pattern_1[len_1 - 1] == pattern_2[len_2 - 1]:
    return 1 + lcs(pattern_1, pattern_2, len_1 - 1, len_2 - 1)
else :
    return max(lcs(pattern_1, pattern_2, len_1 - 1, len_2), lcs(pattern_1, pattern_2, len_1, len_2 - 1))
pattern_1 = "RGBGARGA"
pattern_2 = "BGRARG"
print("Lenght of LCS is: ", lcs(pattern_1, pattern_2, len(pattern_1), len(pattern_2)))

输出

Lenght of LCS is:  5

最长公共子序列（LCS）的动态规划方法

动态规划意味着优化纯粹的递归方法。例如，如果我们查看递归或朴素方法图，我们可以看到有许多相同的函数调用。动态规划方法会将所有计算记录在数组中，并在需要时使用它。

我们将使用一个尺寸为 m x n 的二维数组，其中 m 和 n 分别是模式1和模式2的长度。

对于 [2D 数组](https://guru99.com.cn/python-2d-array.html)，我们可以在 Python 中使用 List 数据结构，或者在 C++ 中使用 vector/array 数据结构。

使用 DP 进行 LCS 的伪代码

LCS(pattern_1, pattern_2):
    m = length of pattern_1 + 1
n = length of pattern_2 + 1
dp[n][m]
for i in range 0 to n + 1:
    for j in range 0 to m + 1:
    if i or j equals to 0:
    dp[i][j] = 0
else if pattern_1[i] == pattern_2[j]:
    dp[i]][j] = dp[i - 1][j - 1] + 1
else :
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[n][m]

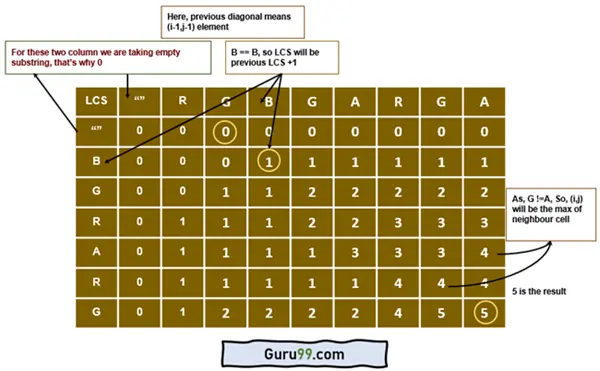
上图是用于动态规划方法的二维数组数据结构 LCS 表。

让我们讨论一下我们在这里使用的逻辑。步骤是：

步骤 1） 如果 i 或 j 为零，我们从给定的两个字符串中取一个空字符串，并尝试查找公共子序列。然而，由于我们取出的子串为空，子序列长度为0。

步骤 2） 如果两个字符匹配，我们将通过增加之前计算的 LCS（位于 (i-1,j-1) 索引处（来自上一行））来为 (i,j) 索引赋值。

步骤 3） 如果不匹配，我们将取相邻两个索引的最大 LCS。就这样，我们需要填充二维数组中的所有值。

步骤 4） 最后，我们将返回二维数组的最后一个单元格的值。

基本上，二维数组中的所有值都包含公共子序列的长度。其中，最后一个单元格包含最长公共子序列的长度。

C++ 实现

#include<iostream>
using namespace std;
int lcs(string pattern_1, string pattern_2) {
  int m = pattern_1.size();
  int n = pattern_2.size();
  // dp will store solutions as the iteration goes on
  int dp[n + 1][m + 1];
  for (int i = 0; i & lt; n + 1; i++) {
    for (int j = 0; j & lt; m + 1; j++) {
      if (i == 0 || j == 0) {
        dp[i][j] = 0;
      } else if (pattern_2[i - 1] == pattern_1[j - 1]) {
        dp[i][j] = dp[i - 1][j - 1] + 1;
      } else {
        dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
      }
    }
  }
  return dp[n][m];
}
int main() {
  string pattern_1 = "RGBGARGA";
  string pattern_2 = "BGRARG";
  cout<<"Length of LCS: "<<lcs(pattern_1, pattern_2)<<endl;
}

输出

Length of LCS: 5

Python 实现

def lcs(pattern_1, pattern_2):
    m = len(pattern_1)
n = len(pattern_2)
# dp will store solutions as the iteration goes on
dp = [
    [None] * (n + 1) for item in range(m + 1)
]
for i in range(m + 1):
    for j in range(n + 1):
    if i == 0 or j == 0:
    dp[i][j] = 0
elif pattern_1[i - 1] == pattern_2[j - 1]:
    dp[i][j] = dp[i - 1][j - 1] + 1
else :
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[m][n]
pattern_1 = "RGBGARGA"
pattern_2 = "BGRARG"
print("Length of LCS: ", lcs(pattern_1, pattern_2))

输出

Length of LCS: 5

因此，两个字符串的最长公共子序列长度都是 5。

总之，我们在 DP 方法中计算每个任务一次。在递归方法中，我们可能有重叠子问题。

在此动态规划算法中，我们使用了一个二维矩阵。将给出两个字符串（假设它们的长度都为 n）。那么数组所需的空间就是 n x n。如果字符串足够大，我们将需要 DP 解决方案的内存优化版本。

代码中采用的简化逻辑是：

声明一个二维数组 DP[m][n]。
用 0 填充 DP 数组的第一行和第一列。
使用 i 和 j 进行迭代。
如果 pattern1[i] 等于 pattern2[j]，则更新 DP[i][j] = DP[i-1][j-1] + 1
如果 pattern1[i] 不等于 pattern2[j]，则 DP[i][j] 将是 DP[i-1][j] 和 DP[i][j-1] 之间的最大值。
一直执行直到 i 和 j 分别达到 m 和 n。
最后一个元素或 DP[m-1][n-1] 将包含长度。

这里，它被表示为 DP[m-1][n-1]，因为数组索引从 0 开始。

摘要

DP 方法的时间复杂度较低，为 O(mn)，其中 m 和 n 是输入字符串或数组的长度。
DP 是比递归方法更快的解决方案，时间复杂度为 **O(n*2^m)。**
动态规划（DP）不是内存优化的。我们使用了一个长度为 m*n 的二维数组。因此，空间复杂度为 (m*n)。
递归方法在最坏情况下，它占用的最大内存将是 m+n，即输入字符串的总长度。
当今的现代计算机足以处理如此大量的内存。

什么是最长公共子序列？

示例

朴素方法

示例

最优子结构

相关文章

最长公共子序列的递归方法

C++ 实现

Python 实现

最长公共子序列（LCS）的动态规划方法

C++ 实现

Python 实现

摘要

订阅新闻通讯