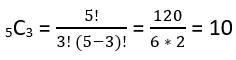组合算法：打印 R 的所有可能组合

什么是组合？

组合是某些给定对象的排列的一种。从数学术语上讲，组合是从一个唯一的项目/对象集合中进行选择的集合。在这里，项目的顺序无关紧要。它也被称为计算事件总结果的方法，其中结果的顺序无关紧要。

例如，你有一个包含 5 种不同颜色的袋子，并被要求生成一种包含任意 3 种颜色的图案。你还可以从 4 种颜色中任意选择 3 种，然后以不同的顺序排列它们。

假设颜色是 RGYBI（R=红色，G=绿色，Y=黄色，B=蓝色，I=靛蓝色）。所以，可能的图案可以是 RGB、RGY 等。

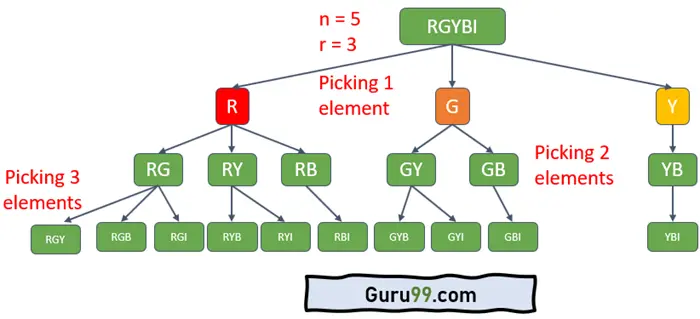
让我们看下图

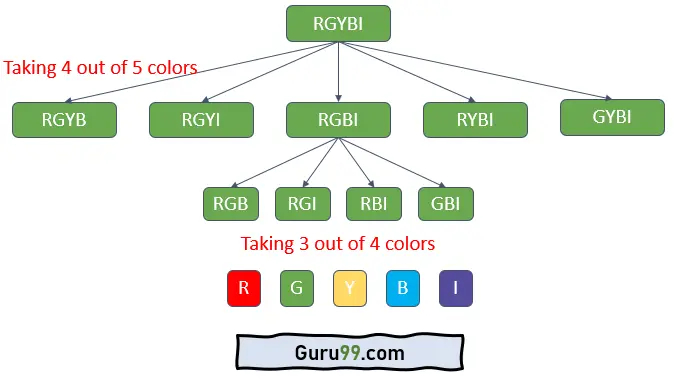
解释

从 5 种颜色中任选 4 种并列出
从每组 4 种颜色中，任意选择 3 种并全部列出。例如，我们在图中只选择了“RGBI”，显示了 4 种组合。
有一个计算我们可以生成的组合总数的理论。从 n 个元素中选择 r 个元素的组合可以数学地表示为

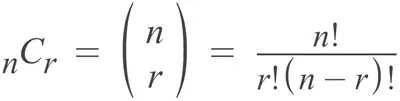
符号“!” 表示阶乘。例如，
N! = N * (N-1) * (N-2) * … * 3 * 2 * 1
例如，5! = 5*4*3*2*1 = 120

所以，对于我们上面的问题，我们有 5 种颜色，意味着 n = 5，而在任何给定时间，我们需要选择 3 种。所以，r = 3。计算后，我们得到，

对于上述场景，总共有 10 种颜色组合是可能的。

组合的时间复杂度分析

现在，假设给定一个大小为 n 的数组，我们被要求从数组中选取 r 个元素并执行 r 个元素的组合。

如果给定一个大小为 n 的数组，那么执行该任务将需要 O(n²) 的时间。此外，如果我们想删除重复项，那么，

我们需要执行以下步骤

步骤 1）按升序对输入数组数据进行排序。排序的时间复杂度为 O(n*log(n))。

步骤 2）创建另一个包含给定临时数组数据中唯一元素的数组。

步骤 3）然后，执行组合函数。

因此，总时间复杂度变为 = O(n²) + O(nLog(n))。我们可以将其视为 O(n²)，因为 n² 远大于 n*log(n)。

方法一：固定元素与递归

在此方法中，我们将选择一个元素，然后查找 r-1 个元素的组合。由于我们是从其余元素中选择一个元素，因此我们是递归进行的，因此称为固定元素和递归。

让我们用图表分步演示算法

步骤如下

步骤 1）在第一层，取 n-r+1 个元素。也就是说，我们取了 3 个元素。

步骤 2）从第二层选择一个元素，并将其向上取到 n-r。所以，如果我们取“R”，那么，与 R 一起，我们可以取 G、Y 和 B。

步骤 3）从第三层选择一个元素，并将其向上取到第 n 个元素，并形成包含 3 个元素的块。

上图是递归的返回值。只有最后一层会被打印。

伪代码

function combination:
pass in: inputArray, combinationArray, start, end, index, r
if index is equal to r:
for each element in combinationArray:
print each element
return
for i = start:
if i <=end and end -i+1 > r-index:
combinationArray[index] = inputArray[i]
call combination function again with updated parameter

C/C++ 实现

#include<bits/stdc++.h>
#include<stdio.h>
void Combination(char inputArray[], char combinationArray[], int start, int end, int index, int r) {
  if (index == r) {
    for (int i = 0; i & lt; r; i++) {
      printf("%c", combinationArray[i]);
    }
    printf("\n");
    return;
  }
  for (int i = start; i & lt; = end & amp; & amp; end - i + 1 & gt; = r - index; i++) {
    combinationArray[index] = inputArray[i];
    Combination(inputArray, combinationArray, i + 1, end, index + 1, r);
  }
}
int main() {
  char inputArray[] = {'R','G','Y','B','I'};
  int n = sizeof(inputArray) / sizeof(inputArray[0]);
  int r = 3;
  char combinationArray[r];
  printf("Combinations:\n");
  Combination(inputArray, combinationArray, 0, n - 1, 0, r);
}

输出

Combinations:
RGY
RGB
RGI
RYB
RYI
RBI
GYB
GYI
GBI
YBI

Python 实现

def Combination(inputArray, combinationArray, start, end, index, r):
    if index == r:
    for item in combinationArray:
    print(item, end = " ")
print()
return
i = start
while (i & lt; = end and end - i + 1 & gt; = r - index):
    combinationArray[index] = inputArray[i]
Combination(inputArray, combinationArray, i + 1, end, index + 1, r)
i += 1
inputArray = "RGYBI"
n = len(inputArray)
r = 3
combinationArray = [0] * r
Combination(inputArray, combinationArray, 0, n - 1, 0, r)

输出

R G Y 
R G B
R G I
R Y B
R Y I
R B I
G Y B
G Y I
G B I
Y B I

方法二（包含和排除每个元素）

此方法基于帕斯卡恒等式。以前我们使用递归来计算 nCr。这里，方法只是除法而不是复杂的循环。

根据帕斯卡恒等式，

nCr = (n-1)Cr + (n-1)C(r-1)

因此，递归算法将有两种递归逻辑来查找给定大小为 n 的数组中的 r 个元素的组合。

元素包含在当前组合中
元素被排除在当前组合之外

伪代码

function combination:
pass in: inputArray, combinationArray, n, r, index, i
if the index is equal to r:
for each element in combination array:
print each element
if i>=n:
return
  combinationArray[index] = inputArray[i]
  combination(inputArray, combinationArray, n, r, index+1, i+1)
  combination(inputArray, combinationArray, n, r, index, i+1)

C/C++ 实现

#include<bits/stdc++.h>
#include<stdio.h>
void Combination(char inputArray[], char combinationArray[], int n, int r, int index, int i) {
  if (index == r) {
    for (int j = 0; j & lt; r; j++) {
      printf("%c", combinationArray[j]);
    }
    printf("\n");
    return;
  }
  if (i & gt; = n)
    return;
  combinationArray[index] = inputArray[i];
  Combination(inputArray, combinationArray, n, r, index + 1, i + 1);
  Combination(inputArray, combinationArray, n, r, index, i + 1);
}
int main() {
  char inputArray[] = {'R','G','Y','B','I'};
  int n = sizeof(inputArray) / sizeof(inputArray[0]);
  int r = 3;
  char combinationArray[r];
  printf("Combinations:\n");
  Combination(inputArray, combinationArray, n, r, 0, 0);
}

输出

Combinations:
RGY
RGB
RGI
RYB
RYI
RBI
GYB
GYI
GBI
YBI

Python 实现

def Combination(inputArray, combinationArray, n, r, index, i):
    if index == r:
    for item in combinationArray:
    print(item, end = " ")
print()
return
if i & gt; = n:
    return
combinationArray[index] = inputArray[i]
Combination(inputArray, combinationArray, n, r, index + 1, i + 1);
Combination(inputArray, combinationArray, n, r, index, i + 1);
inputArray = "RGYBI"
n = len(inputArray)
r = 3
combinationArray = [""] * r
Combination(inputArray, combinationArray, n, r, 0, 0)

输出

R G Y
R G B
R G I
R Y B
R Y I
R B I
G Y B
G Y I
G B I
Y B I

处理重复组合

有时输入数组中可能存在重复元素。

例如，

输入数组包含 n = {5, 2, 3, 1, 5}。
这里，我们可以看到 5 出现了 2 次。
现在，如果我们想为这个数组运行代码，一些组合将被重复。
我们将找到 {5, 2, 5}、{5, 2, 3} 等，或者任何包含 5 的组合将被重复。

我们可以使用这两种方法

对输入数组进行排序。排序需要 O(nlog(n)) 时间。
然后增加 i 的值，同时 i 的值和 i+1 的值是相同的。基本上将以下两行代码放入组合函数中。

// For c/c++
while(inputArray[i] == inputArray[i+1]){
  i++;
}

# for python
  while inputArray[i]==inputArray[i+1]:
    i+=1

使用字典或无序映射来跟踪重复组合

所以，如果我们不想对元素进行排序来跟踪重复项，我们可以遵循给定的步骤。

步骤 1）声明一个全局字典或哈希映射。
步骤 2）将生成的组合推送到哈希映射中，并将其值加一。组合是键，它们的出现次数是值。
步骤 3）当函数运行完毕后，我们只需从哈希映射或字典中打印所有键。

这是 python 中的实现

unique_combination = dict()
def Combination(inputArray, combinationArray, n, r, index, i):
    if index == r:
    temp_combination = ""
for item in combinationArray:
    temp_combination += item
unique_combination[temp_combination] = unique_combination.get(temp_combination, 0) + 1
return
if i & gt; = n:
    return
combinationArray[index] = inputArray[i]
Combination(inputArray, combinationArray, n, r, index + 1, i + 1);
Combination(inputArray, combinationArray, n, r, index, i + 1);
inputArray = "RGYBIB"
n = len(inputArray)
r = 3
combinationArray = [""] * r
Combination(inputArray, combinationArray, n, r, 0, 0)
for item in unique_combination.keys():
    print(item)

输出

RGY
RGB
RGI
RYB
RYI
RBI
RBB
RIB
GYB
GYI
GBI
GBB
GIB
YBI
YBB
YIB
BIB

这里，您可以看到输入是“RGYBIB”。通常，会出现一些重复的组合。但是由于我们使用了字典并将每个组合视为键，因此我们可以只打印唯一的组合。

现在，如果您输入“print(unique_combination)”，您将看到每个组合的频率。它会显示如下

{'RGY': 1, 'RGB': 2, 'RGI': 1, 'RYB': 2, 'RYI': 1, 'RBI': 1, 'RBB': 1, 'RIB': 1, 'GYB': 2, 'GYI': 1, 'GBI': 1, 'GBB': 1, 'GIB': 1, 'YBI': 1, 'YBB': 1, 'YIB': 1, 'BIB': 1}

所以，我们可以看到 RGB、RYB、GYB 出现了 2 次。将键插入字典的时间复杂度基本上是 O(1)。因此，如果您使用字典，那么运行代码的总时间复杂度将是

O(1) + O(n*n)

相当于 O(n*n)。

使用前一种方法来跟踪重复项，我们需要 O(n*log(n)) 来排序；为了比较，我们需要 O(n)，而函数本身需要 O(n*n)。总时间复杂度将是

O(n*log(n)) + O(n) +O(n*n)

什么是组合？

组合的时间复杂度分析

方法一：固定元素与递归

伪代码

C/C++ 实现

Python 实现

相关文章

方法二（包含和排除每个元素）

伪代码

C/C++ 实现

Python 实现

处理重复组合

使用字典或无序映射来跟踪重复组合

这是 python 中的实现

订阅新闻通讯