拓扑排序:Python、C++ 算法示例
什么是拓扑排序算法?
拓扑排序也称为 Kahn 算法,是一种流行的排序算法。使用有向图作为输入,拓扑排序会对节点进行排序,使得每个节点都出现在其指向的节点之前。
此算法应用于 DAG(有向无环图),以便每个节点都出现在有序数组中,并且所有其他节点都指向它。此算法会重复遵循一些规则,直到排序完成。
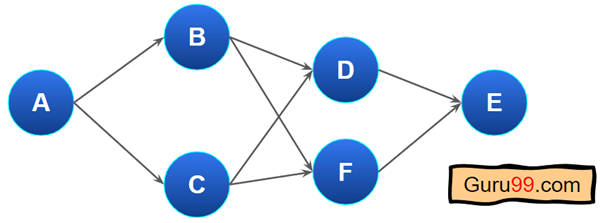
为了简化,请看下面的示例
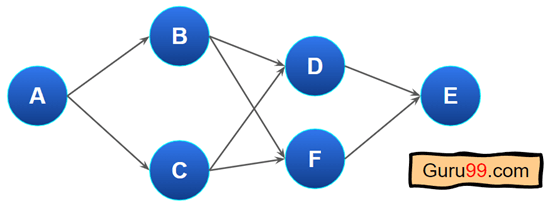
这里,我们可以看到“A”没有入度。它表示指向节点的边。“B”和“C”的前提是“A”,然后“E”的前提是“D”和“F”节点。有些节点依赖于其他节点。
这是上述图形的另一种表示形式
因此,当我们把 DAG(有向无环图)传递给拓扑排序时,它会给我们一个具有线性排序的数组,其中第一个元素没有依赖项。
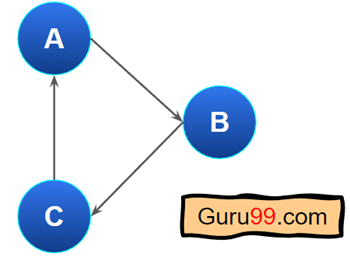
此示例显示了一个带有循环的图形
以下是执行此操作的步骤
步骤 1) 找到入度为零的节点,即度为零的节点。
步骤 2) 将零入度节点存储在队列或栈中,并从图形中删除该节点。
步骤 3) 然后删除该节点的出边(传出边)。
这将递减下一个节点的入度计数。
拓扑排序要求图数据结构不包含任何循环。
如果图遵循这些要求,则该图被认为是 DAG
- 一个或多个节点的入度值为零。
- 图不包含任何循环
只要图中还有节点并且图仍然是 DAG,我们就会执行上述三个步骤。否则,算法将陷入循环依赖,Kahn 算法将无法找到一个入度为零的节点。
拓扑排序的工作原理
在这里,我们将使用“Kahn 算法”进行拓扑排序。假设我们有以下图形
以下是 Kahn 算法的步骤
步骤 1) 计算图中所有节点的入度或传入边。
注意
- 入度表示指向节点的有向边。
- 出度表示从节点出来的有向边。
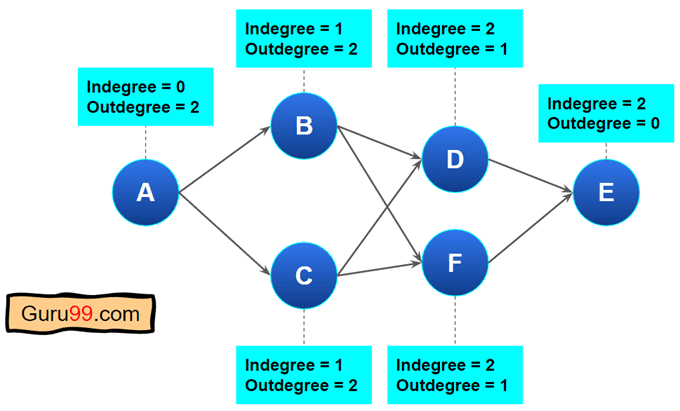
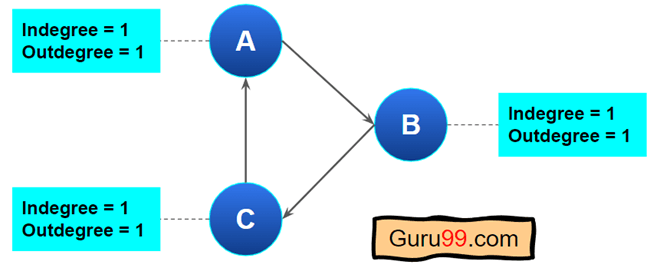
这是上述图形的入度和出度
步骤 2) 找到入度为零或传入边为零的节点。
入度为零的节点意味着没有边指向该节点。节点“A”的入度为零,这意味着没有边指向节点“A”。
因此,我们将执行以下操作
- 删除此节点及其出度边(传出边)
- 将节点放入队列以进行排序。
- 更新“A”的邻居节点的入度计数。
步骤 3) 我们需要找到一个入度值为零的节点。在此示例中,“B”和“C”的入度为零。
在这里,我们可以选择其中任何一个。我们选择“B”并将其从图中删除。
然后更新其他节点的入度值。
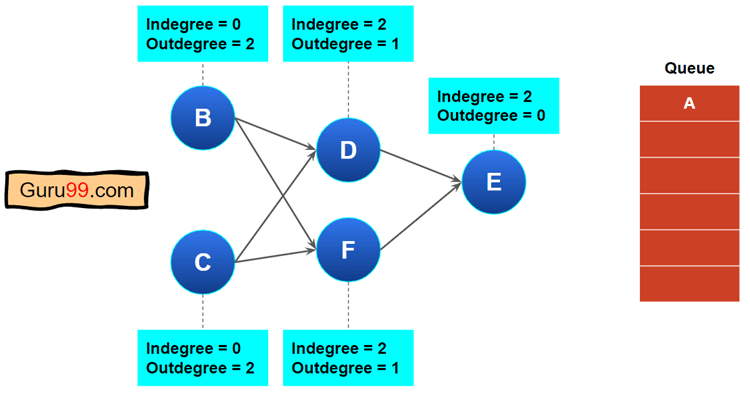
执行这些操作后,我们的图形和队列将如下所示
步骤 4) 节点“C”没有传入边。因此,我们将从图中删除节点“C”并将其推入队列。
我们也可以删除从“C”传出的边。
现在,我们的图形将如下所示
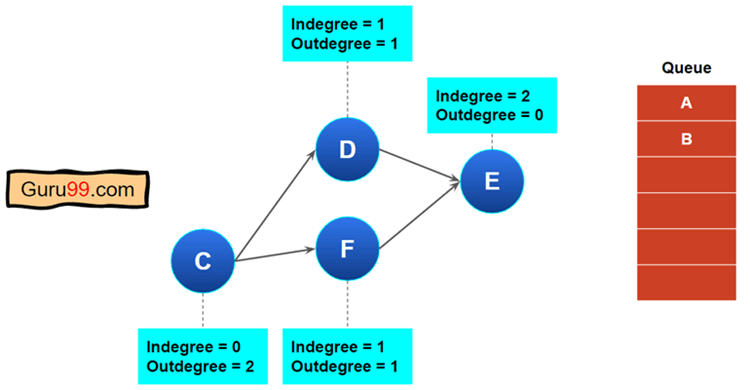
步骤 5) 我们可以看到节点“D”和“F”的入度为零。我们将选择一个节点并将其放入队列。
我们先取出“D”。然后节点“E”的入度计数将为 1。现在,从 D 到 E 将没有节点。
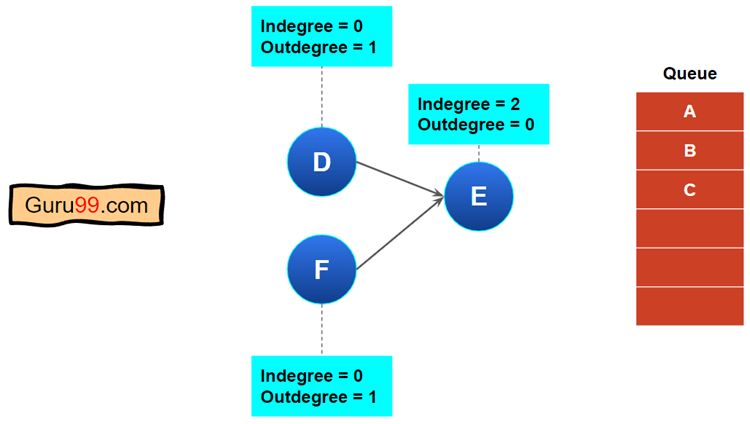
我们需要对节点“F”执行相同的操作,我们的结果将如下所示
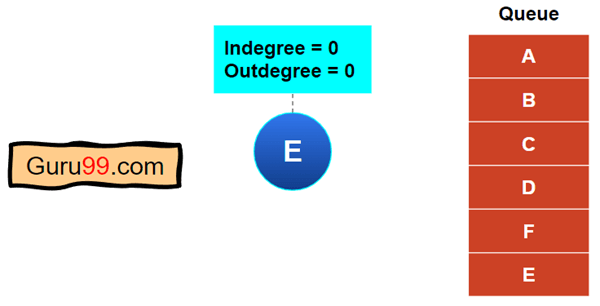
步骤 6) 节点“E”的入度(传入边)和出度(传出边)都变为零。因此,我们已经满足了节点“E”的所有前提条件。
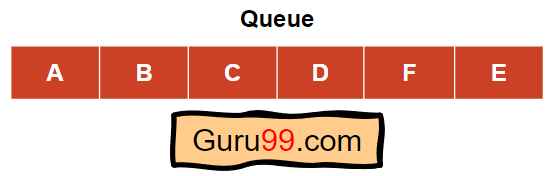
在这里,我们将“E”放在队列的末尾。所以,没有剩余的节点了,算法在这里结束。
拓扑排序的伪代码
以下是使用 Kahn 算法进行拓扑排序的伪代码。
function TopologicalSort( Graph G ):
for each node in G:
calculate the indegree
start = Node with 0 indegree
G.remove(start)
topological_list = [start]
While node with O indegree present:
topological_list.append(node)
G.remove(node)
Update Indegree of present nodes
Return topological_list
拓扑排序也可以使用 DFS(深度优先搜索)方法来实现。但是,该方法是递归方法。Kahn 算法比 DFS 方法更有效。
C++ 拓扑排序实现
#include<bits/stdc++.h>
using namespace std;
class graph{
int vertices;
list<int> *adjecentList;
public:
graph(int vertices){
this->vertices = vertices;
adjecentList = new list<int>[vertices];
}
void createEdge(int u, int v){
adjecentList[u].push_back(v);
}
void TopologicalSort(){
// filling the vector with zero initially
vector<int> indegree_count(vertices,0);
for(int i=0;i<vertices;i++){
list<int>::iterator itr;
for(itr=adjecentList[i].begin(); itr!=adjecentList[i].end();itr++){
indegree_count[*itr]++;
}
}
queue<int> Q;
for(int i=0; i<vertices;i++){
if(indegree_count[i]==0){
Q.push(i);
}
}
int visited_node = 0;
vector<int> order;
while(!Q.empty()){
int u = Q.front();
Q.pop();
order.push_back(u);
list<int>::iterator itr;
for(itr=adjecentList[u].begin(); itr!=adjecentList[u].end();itr++){
if(--indegree_count[*itr]==0){
Q.push(*itr);
}
}
visited_node++;
}
if(visited_node!=vertices){
cout<<"There's a cycle present in the Graph.\nGiven graph is not DAG"<<endl;
return;
}
for(int i=0; i<order.size();i++){
cout<<order[i]<<"\t";
}
}
};
int main(){
graph G(6);
G.createEdge(0,1);
G.createEdge(0,2);
G.createEdge(1,3);
G.createEdge(1,5);
G.createEdge(2,3);
G.createEdge(2,5);
G.createEdge(3,4);
G.createEdge(5,4);
G.TopologicalSort();
}
输出
0 1 2 3 5 4
Python 拓扑排序实现
from collections import defaultdict
class graph:
def __init__(self, vertices):
self.adjacencyList = defaultdict(list)
self.Vertices = vertices # No. of vertices
# function to add an edge to adjacencyList
def createEdge(self, u, v):
self.adjacencyList[u].append(v)
# The function to do Topological Sort.
def topologicalSort(self):
total_indegree = [0]*(self.Vertices)
for i in self.adjacencyList:
for j in self.adjacencyList[i]:
total_indegree[j] += 1
queue = []
for i in range(self.Vertices):
if total_indegree[i] == 0:
queue.append(i)
visited_node = 0
order = []
while queue:
u = queue.pop(0)
order.append(u)
for i in self.adjacencyList[u]:
total_indegree[i] -= 1
if total_indegree[i] == 0:
queue.append(i)
visited_node += 1
if visited_node != self.Vertices:
print("There's a cycle present in the Graph.\nGiven graph is not DAG")
else:
print(order)
G = graph(6)
G.createEdge(0,1)
G.createEdge(0,2)
G.createEdge(1,3)
G.createEdge(1,5)
G.createEdge(2,3)
G.createEdge(2,5)
G.createEdge(3,4)
G.createEdge(5,4)
G.topologicalSort()
输出
[0, 1, 2, 3, 5, 4]
拓扑排序算法的循环图
包含循环的图无法进行拓扑排序。因为循环图具有循环依赖。
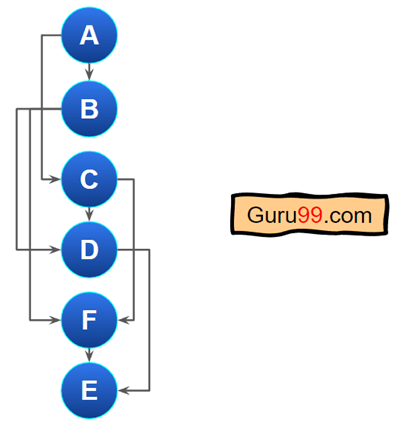
例如,请查看此图形
该图形不是 DAG(有向无环图),因为 A、B 和 C 构成了循环。如果您注意到,没有一个节点的入度值为零。
根据 Kahn 算法,如果我们分析上述图形
- 找到一个入度为零(无传入边)的节点。
- 从图中删除该节点并将其推入队列。
但是,在上图中,没有一个节点的入度为零。每个节点的入度值都大于 0。 - 返回一个空队列,因为它找不到任何入度为零的节点。
我们可以使用以下步骤通过拓扑排序检测循环
步骤 1) 执行拓扑排序。
步骤 2) 计算拓扑排序列表中的元素总数。
步骤 3) 如果元素数量等于顶点总数,则没有循环。
步骤 4) 如果不等于顶点数量,则给定图数据结构中至少有一个循环。
拓扑排序的复杂度分析
算法中有两种类型的复杂度。它们是
- 时间复杂度
- 空间复杂度
这些复杂度用一个提供通用复杂度的函数表示。
时间复杂度:拓扑排序的所有时间复杂度都相同。时间复杂度存在最坏、平均和最佳情况。
拓扑排序的时间复杂度为 O(E + V),其中 E 表示图中的边数,V 表示图中的顶点数。
让我们分解一下这个复杂度
步骤 1) 在开始时,我们将计算所有入度。为此,我们需要遍历所有边,最初,我们将所有 V 个顶点的入度设置为零。因此,我们完成的增量步骤将是 O(V+E)。
步骤 2) 我们将找到入度值为零的节点。我们需要从 V 个顶点中搜索。因此,完成的步骤将是 O(V)。
步骤 3) 对于每个入度为零的节点,我们将删除该节点并递减入度。对所有节点执行此操作将花费 O(E)。
步骤 4) 最后,我们将检查是否存在循环。我们将检查排序数组中的元素总数是否等于节点总数。这将花费 O(1)。
所以,这些是拓扑排序或拓扑排序每个步骤的单独时间复杂度。我们可以说,从上面的计算得出的时间复杂度将是 O( V + E );这里,O 是复杂度函数。
空间复杂度:运行拓扑排序算法需要 O(V) 的空间。
以下是我们在此程序中需要空间的步骤
- 我们需要计算图中所有节点的入度。由于图总共有 V 个节点,因此我们需要创建一个大小为 V 的数组。因此,所需空间为 O(V)。
- 使用了队列数据结构来存储入度为零的节点。我们从原始图中删除了入度为零的节点,并将它们放入队列中。为此,所需空间为 O(V)。
- 名为“order”的数组。它以拓扑顺序存储节点。这也需要 O(V) 的空间。
这些是各个空间复杂度。因此,我们需要在运行时最大化这些空间。
空间复杂度为 O(V),其中 V 表示图中顶点的数量。
拓扑排序的应用
拓扑排序有很多用途。以下是一些
- 当 操作系统 需要执行资源分配时,它会被使用。
- 在图中查找循环。我们可以使用拓扑排序来验证图是 DAG 还是非 DAG。
- 自动补全应用程序中的句子排序。
- 它用于检测 死锁。
- 不同类型的调度或课程调度使用拓扑排序。
- 解决依赖关系。例如,如果您尝试安装一个包,该包可能还需要其他包。拓扑排序可以找出安装当前包所需的所有必要包。
- Linux 在“apt”中使用拓扑排序来检查包的依赖关系。