Kadence 算法:最大子数组和
什么是最大的连续子数组和?
子数组是数组的连续部分。它可以是数组的单个元素,也可以是数组的一部分。最大的连续子数组和意味着具有最大和值的子数组。
例如,一个数组是{-10, 5, 1, 6, -9, 2, -7, 3, -5}。它的子数组可以是:{-10,5,1,6}或{5,1,6}或{2,7,3, -5}等。但{5,1,6,3}不能是子数组,因为它们不保持序列。
如果您注意到,在所有子数组中,以下突出显示的子数组(5,1,6)具有最大的求和值。
子数组 {5,1,6} 的和 = 11,是上述数组所有可能的子数组组合中的最大和。因此,对于上述数组,最大子数组是 {5,1,6}。
Kadence 算法:最大子数组和
求解最大连续子数组和的简单方法
解决这个问题的简单方法是使用两个循环来查找所有子数组,计算它们的和,然后找到最大值。
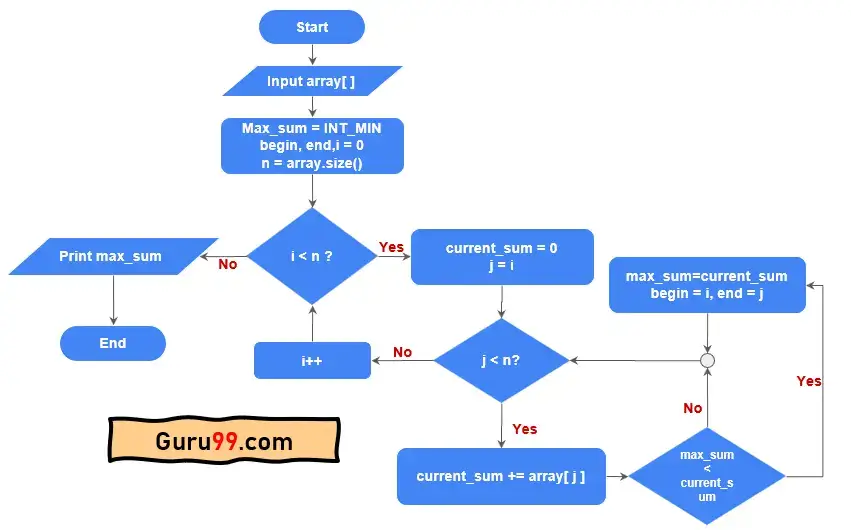
这是查找最大连续子数组和的简单方法的流程图。这是一种蛮力方法,因为我们遍历了所有可能的子数组。
以下是执行此操作的简单步骤。
步骤 1) 将 max_sum 初始化为最小整数值,并将变量“begin”和“end”设置为零。
步骤 2) 令 i 和 j 为数组的索引,其中“j”大于等于“i”。i 代表子数组的起始索引,j 代表子数组的结束索引。
步骤 3) “Current_sum”将保存子数组的和。计算当前和后,检查 current_sum 是否大于 max_sum。
步骤 4) 如果 current_sum 更大,则将 max_sum 替换为当前和。
步骤 5) 检查“j”是否已到达数组末尾。如果“j”已到达数组末尾,则增加“i”并将 current_sum 值更改为 0。
步骤 6) 执行所有这些步骤,直到“i”到达数组末尾。
步骤 7) 在这两个循环结束后,max_sum 将保存最大的子数组和。
简单方法的伪代码
function maximumSubarraySum():
input: array
for all possible subArray from array:
calculate sum of each sub array
store the maximum subArray
return the maximum sum
简单方法的C++实现
#include <stdio.h>
#include <iostream>
using namespace std;
void maximumSubarraySum(int array[], int n) {
int max_sum = -1e9;
int begin = 0;
int end = 0;
for (int i = 0; i < n; i++) {
int current_sum = 0;
for (int j = i; j < n; j++) {
current_sum += array[j];
if (max_sum < current_sum) {
max_sum = current_sum;
begin = i;
end = j;
}
}
}
cout << "largest sum is " << max_sum << endl;
cout << "largest sum contiguous subarray: ";
for (int i = begin; i <= end; i++) {
cout << array[i] << "\t";
}
}
int main() {
int array[] = {-10, 5, 1, 6, -9, 2, -7, 3, -5};
maximumSubarraySum(array, sizeof(array) / sizeof(array[0]));
}
输出
largest sum is 12 largest sum contiguous subarray: 5 1 6
简单方法的Python实现
def maximumSubarraySum(numbers):
max_sum,begin,end = -1e9, 0 , 0
for i in range(len(numbers)):
current_sum=0
for j in range(i,len(numbers)):
current_sum+=numbers[j]
if max_sum<current_sum:
max_sum=current_sum
begin,end=i,j
print("largest sum is ",max_sum)
print("largest sum contiguous subarray: ",end="")
for i in range(begin,end+1):
print(numbers[i],end='\t')
numbers = [-10,5,1,6,-9,2,-7,3,-5]
maximumSubarraySum(numbers)
输出
largest sum is 12 largest sum contiguous subarray: 5 1 6
Kadane 算法寻找最大连续子数组和
Kadane 算法是一种“动态规划”方法。这里我们使用一个循环而不是两个循环。Kadane 算法的通用实现仅适用于正数数组。
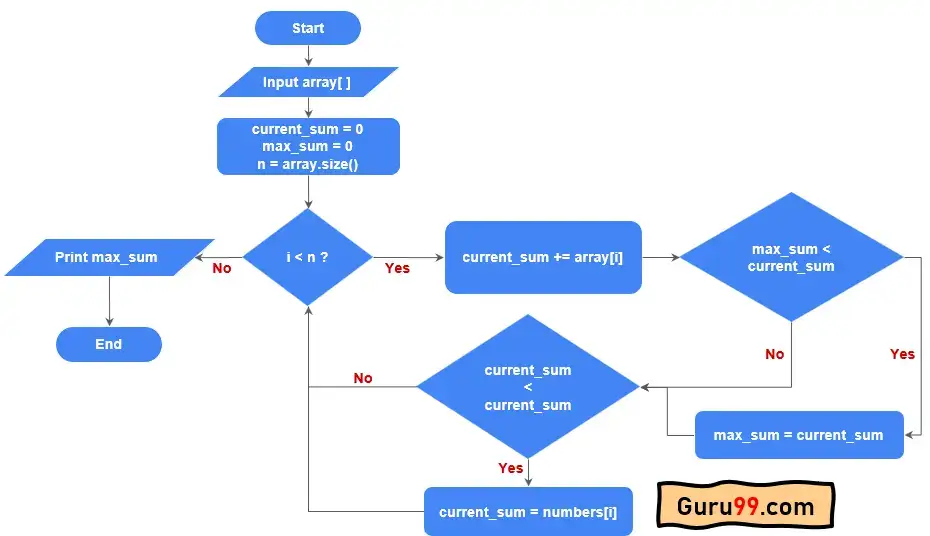
我们只需要两个变量来找到最大的连续子数组和。这是 Kadane 算法的流程图。
以下是 Kadane 算法的步骤。
步骤 1) 创建两个变量:current_sum 和 max_sum。
“Current_sum”将保存以特定数组索引结尾的最大和值,而“max_sum”将保存到目前为止的最大求和值。
步骤 2) 我们将每个数组元素的值加到 current_sum 中。然后我们将检查以下两个条件:
- 如果 current_sum 小于当前元素,则 current_sum 值将为当前元素。
- 如果 max_sum 小于 current_sum,则 max_sum 将为 current_sum。
步骤 3) 对整个数组执行上一步,我们将在“max_sum”变量中得到最大的连续子数组和。
Kadane 算法示例
我们将使用一个小尺寸数组演示 Kadane 算法,并讨论查找最大连续子数组和的每个步骤。
假设给定的数组如下所示:
以下是 Kadane 算法的步骤:
步骤 1) 创建两个变量:current_sum 和 max_sum。将 max_sum 设置为 INT_MIN,将 current_sum 设置为零。(此处,INT_MIN 表示最小整数数)。
步骤 2) 在索引 0 处,值为 4。所以,current_sum = 0 + 4 或 4。此时 current_sum 大于 max_sum,max_sum 将为 4。
步骤 3) 在索引 1 处,值为 -2。所以,current_sum = 4 + (-2) 或 2。
此时 current_sum 小于 max_sum。因此,max_sum 的值不会被更新。
步骤 4) 下一个值是 1。如果我们将其与 current_sum 相加,则 current_sum 将为 3。此时 max_sum 仍然大于 current_sum。因此,max_sum 不会更新。
步骤 5) 在索引 3 处,值为 3。我们将通过将 current_sum 增加 3 来更新值。所以,current_sum 将为 6。
在这种情况下,max_sum 小于 current_sum。因此,max_sum 将被 current_sum 的值更新。
步骤 6) 对于数组的最后一个元素,我们有 -1。如果我们将其与 current_sum 相加,current_sum 将为 5,小于 max_sum。因此,max_sum 将保持为 6。
我们已经到达了数组的末尾,算法在此结束。现在,“max_sum”包含最大的子数组和。即 5。子数组是 {4,-2,1,3}。
Kadane 算法的伪代码
function KadaneAlgorithm():
input: array
maximum_sum, current_sum = 0
for each elements in array:
add the element with current_sum
if current_sum is greater than the maximum_sum
then maximum_sum = current_sum
if current_sum is less than the element
then current_sum = element
return the value of maximum_sum
Kadane 算法的 C++ 实现
#include < iostream >
using namespace std;
void kadane(int array[], int n) {
int current_sum = 0;
int max_sum = -1e9;
// -1e9 means -10000000
for (int i = 0; i < n; i++) {
current_sum += array[i];
if (max_sum < current_sum) {
max_sum = current_sum;
}
if (current_sum < array[i]) {
current_sum = array[i];
}
}
cout << "largest sum is " << max_sum << endl;
}
int main() {
int array[] = {-10, 5, 1, 6, -9, 2, -7, 3, -5};
kadane(array, sizeof(array) / sizeof(array[0]));
}
输出
largest sum is 12
Kadane 算法的 Python 实现
def kadane(numbers):
current_sum = 0
max_sum = -1e9
for i in range(len(numbers)):
current_sum += numbers[i]
if max_sum < current_sum:
max_sum = current_sum
if current_sum<numbers[i]:
current_sum = numbers[i]
print("largest sum is ",max_sum)
kadane([-10,5,1,6,-9,2,-7,3,-5])
输出
largest sum is 12
最大连续子数组和的复杂度分析
简单方法使用两个循环。该方法计算所有可能的子数组和以找到最大的一个。这是一种蛮力方法。每个循环都会运行直到数组的末尾。
如果一个数组总共有 N 个元素,那么使用两个循环,我们将遍历 N2 个元素。因此,查找最大连续子数组和的简单方法的 time complexity 将是 O(N2)。这里,“O”表示复杂度函数。
另一方面,Kadane 算法是用于查找最大连续子数组和的动态规划方法。如果您遵循示例或代码,您会发现我们只使用了一个循环。
因此,如果输入数组的大小为 N,则 Kadane 算法的时间复杂度为 O(N)。这比简单方法更快。例如,一个包含 100 个元素的数组。简单方法将需要 100*100 或 10,000 个 CPU 时间。但 Kadane 算法只需要 100 个 CPU 时间。