R 逐步和多元线性回归 [分步示例]
Evelyn Clarke R中的简单线性回归
线性回归回答了一个简单的问题：你能衡量一个目标变量和一个预测变量集之间的确切关系吗？
最简单的概率模型是直线模型
其中
- y = 因变量
- x = 自变量
-
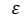= 随机误差分量 -
= 截距 -
= x的系数
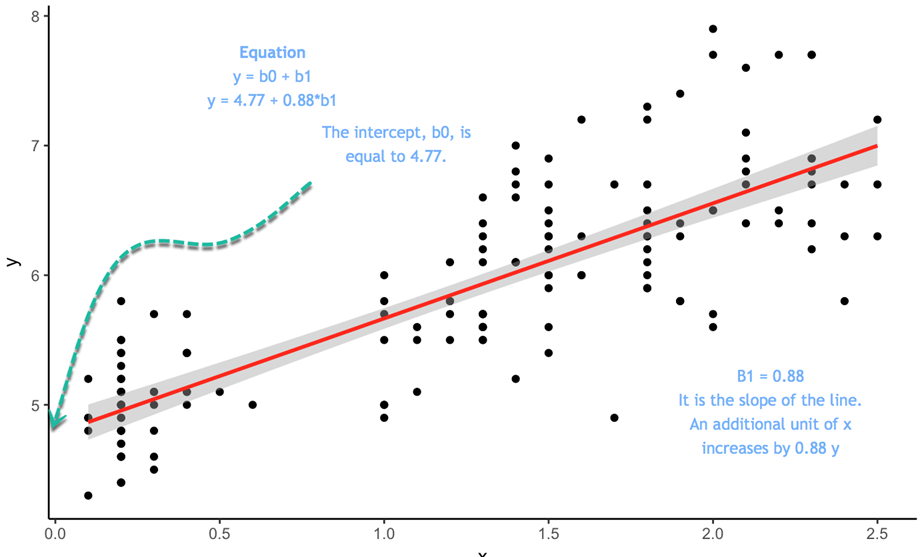
考虑以下图
方程为：
是截距。如果x等于0，y将等于截距4.77。是直线的斜率。它告诉我们y随x变化而变化的比例。
为了估计最佳值
和
您将使用一种称为最小二乘法 (OLS) 的方法。此方法尝试查找最小化误差平方和的参数，即预测的 y 值与实际的 y 值之间的垂直距离。该差值称为误差项。
在估计模型之前，您可以通过绘制散点图来确定 y 和 x 之间的线性关系是否合理。
散点图
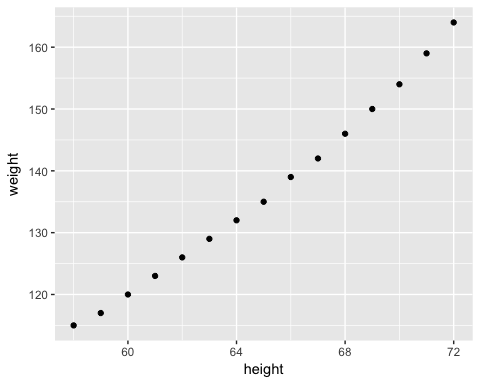
我们将使用一个非常简单的数据集来解释简单线性回归的概念。我们将导入美国女性的平均身高和体重。该数据集包含 15 个观测值。您想衡量身高是否与体重正相关。
library(ggplot2) path <- 'https://raw.githubusercontent.com/guru99-edu/R-Programming/master/women.csv' df <-read.csv(path) ggplot(df,aes(x=height, y = weight))+ geom_point()
输出
散点图表明，随着 x 的增加，y 普遍呈现增加的趋势。在下一步中，您将衡量每增加一个单位，y 会增加多少。
最小二乘估计
在简单的 OLS 回归中，计算
和很简单。本教程的目的不是展示推导过程。您只会写出公式。
您想估计：
OLS 回归的目标是最小化以下方程：
其中
是实际值，而
是预测值。
的解是
请注意，
表示 x 的平均值
的解
是
在 R 中，您可以使用 cov() 和 var() 函数来估计您可以使用 mean() 函数来估计
beta <- cov(df$height, df$weight) / var (df$height) beta
输出
##[1] 3.45
alpha <- mean(df$weight) - beta * mean(df$height) alpha
输出
## [1] -87.51667
beta 系数表明，每增加一英寸身高，体重就会增加 3.45。
手动估计简单线性方程并不理想。R 提供了一个合适的函数来估计这些参数。您很快就会看到这个函数。在此之前，我们将介绍如何手动计算简单线性回归模型。在您作为数据科学家的旅程中，您几乎不会估计简单线性模型。在大多数情况下，回归任务是在许多估计量上执行的。
R中的多元线性回归
回归分析更实际的应用是使用比简单直线模型更复杂的模型。包含一个以上自变量的概率模型称为多元回归模型。该模型的一般形式是
在矩阵表示法中，您可以重写模型
因变量 y 现在是 k 个自变量的函数。系数
确定自变量
和.
我们简要介绍一下我们对 OLS 随机误差 的假设
- 均值为 0
- 方差等于
- 正态分布
- 随机误差是独立的（从概率意义上讲）
您需要求解回归系数向量，该向量使预测值与实际 y 值之间的平方误差和最小化。
闭式解为
与
- 表示矩阵 X 的转置
表示可逆矩阵
表示可逆矩阵我们使用 mtcars 数据集。您已经熟悉该数据集。我们的目标是预测相对于一组特征的每加仑英里数。
R中的连续变量
目前，我们只使用连续变量，而将分类特征放在一边。变量 am 是一个二元变量，如果变速器是手动则取值为 1，如果是自动则取值为 0；vs 也是一个二元变量。
library(dplyr) df <- mtcars % > % select(-c(am, vs, cyl, gear, carb)) glimpse(df)
输出
## Observations: 32 ## Variables: 6 ## $ mpg <dbl> 21.0, 21.0, 22.8, 21.4, 18.7, 18.1, 14.3, 24.4, 22.8, 19.... ## $ disp <dbl> 160.0, 160.0, 108.0, 258.0, 360.0, 225.0, 360.0, 146.7, 1... ## $ hp <dbl> 110, 110, 93, 110, 175, 105, 245, 62, 95, 123, 123, 180, ... ## $ drat <dbl> 3.90, 3.90, 3.85, 3.08, 3.15, 2.76, 3.21, 3.69, 3.92, 3.9... ## $ wt <dbl> 2.620, 2.875, 2.320, 3.215, 3.440, 3.460, 3.570, 3.190, 3... ## $ qsec <dbl> 16.46, 17.02, 18.61, 19.44, 17.02, 20.22, 15.84, 20.00, 2...
您可以使用 lm() 函数来计算参数。此函数的基本语法是
lm(formula, data, subset) Arguments: -formula: The equation you want to estimate -data: The dataset used -subset: Estimate the model on a subset of the dataset
请记住，方程的形式如下：
在 R 中
- 符号 = 被 ~ 替换
- 每个 x 都被变量名替换
- 如果要删除常数项，请在公式末尾添加 -1
示例
您想根据身高和收入来估计个人的体重。方程是
R 中的方程写法如下：
y ~ X1+ X2+…+Xn # 带截距
所以对于我们的例子
- 体重 ~ 身高 + 收入
您的目标是根据一组变量来估计每加仑英里数。要估计的方程是
您将估计您的第一个线性回归，并将结果存储在 fit 对象中。
model <- mpg~.disp + hp + drat + wt fit <- lm(model, df) fit
代码解释
- model <- mpg ~. disp + hp + drat+ wt: 将模型存储以供估算
- lm(model, df): 使用数据框 df 估算模型
## ## Call: ## lm(formula = model, data = df) ## ## Coefficients: ## (Intercept) disp hp drat wt ## 16.53357 0.00872 -0.02060 2.01577 -4.38546 ## qsec ## 0.64015
输出没有提供足够的信息来评估拟合度。您可以使用 summary() 函数访问更多详细信息，例如系数的显着性、自由度和残差的形状。
summary(fit)
输出
## return the p-value and coefficient ## ## Call: ## lm(formula = model, data = df) ## ## Residuals: ## Min 1Q Median 3Q Max ## -3.5404 -1.6701 -0.4264 1.1320 5.4996 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 16.53357 10.96423 1.508 0.14362 ## disp 0.00872 0.01119 0.779 0.44281 ## hp -0.02060 0.01528 -1.348 0.18936 ## drat 2.01578 1.30946 1.539 0.13579 ## wt -4.38546 1.24343 -3.527 0.00158 ** ## qsec 0.64015 0.45934 1.394 0.17523 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 2.558 on 26 degrees of freedom ## Multiple R-squared: 0.8489, Adjusted R-squared: 0.8199 ## F-statistic: 29.22 on 5 and 26 DF, p-value: 6.892e-10
从上述表格输出中进行的推断
- 上表证明了 wt 和里程之间存在很强的负相关关系，而与 drat 之间存在正相关关系。
- 只有变量 wt 对 mpg 有统计学上的影响。请记住，在统计学中检验假设，我们使用
- H0：无统计学影响
- H3：预测变量对 y 有有意义的影响
- 如果 p 值小于 0.05，则表示该变量在统计学上是显着的
- 调整后的 R 方：模型解释的方差。在您的模型中，模型解释了 y 方差的 82%。R 方值始终在 0 到 1 之间。越高越好
您可以使用 anova() 函数运行 ANOVA 检验来估计每个特征对这些方差的影响。
anova(fit)
输出
## Analysis of Variance Table ## ## Response: mpg ## Df Sum Sq Mean Sq F value Pr(>F) ## disp 1 808.89 808.89 123.6185 2.23e-11 *** ## hp 1 33.67 33.67 5.1449 0.031854 * ## drat 1 30.15 30.15 4.6073 0.041340 * ## wt 1 70.51 70.51 10.7754 0.002933 ** ## qsec 1 12.71 12.71 1.9422 0.175233 ## Residuals 26 170.13 6.54 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
估计模型性能的更常规方法是显示残差与不同度量的关系。
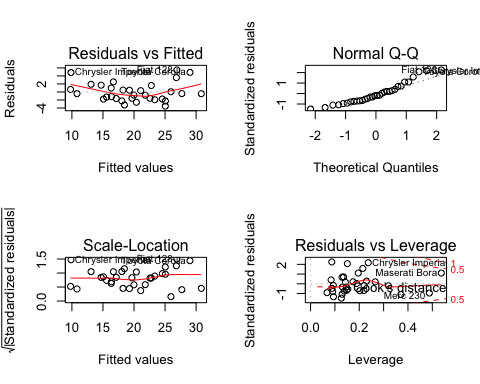
您可以使用 plot() 函数显示四个图形
– 残差与拟合值
– 正态 Q-Q 图：理论四分位数与标准化残差
– 尺度-位置图：拟合值与标准化残差的平方根
– 残差与杠杆值：杠杆值与标准化残差
在 plot(fit) 之前添加代码 par(mfrow=c(2,2))。如果您不添加此行代码，R 会提示您按 Enter 键显示下一个图形。
par(mfrow=(2,2))
代码解释
- (mfrow=c(2,2))：返回一个窗口，其中四个图形并排显示。
- 前两个数字添加行数
- 第二两个数字添加列数。
- 如果写 (mfrow=c(3,2))：您将创建一个 3 行 2 列的窗口
plot(fit)
输出
lm() 公式返回一个包含许多有用信息的列表。您可以使用创建的 fit 对象，后跟 $ 符号和您想提取的信息来访问它们。
– 系数：`fit$coefficients`
– 残差：`fit$residuals`
– 拟合值：`fit$fitted.values`
R中的因子回归
在最后的模型估计中，您仅对连续变量进行 mpg 回归。将因子变量添加到模型中很简单。将变量 am 添加到模型中。确保该变量是因子水平而不是连续变量很重要。
df <- mtcars % > %
mutate(cyl = factor(cyl),
vs = factor(vs),
am = factor(am),
gear = factor(gear),
carb = factor(carb))
summary(lm(model, df))
输出
## ## Call: ## lm(formula = model, data = df) ## ## Residuals: ## Min 1Q Median 3Q Max ## -3.5087 -1.3584 -0.0948 0.7745 4.6251 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 23.87913 20.06582 1.190 0.2525 ## cyl6 -2.64870 3.04089 -0.871 0.3975 ## cyl8 -0.33616 7.15954 -0.047 0.9632 ## disp 0.03555 0.03190 1.114 0.2827 ## hp -0.07051 0.03943 -1.788 0.0939 . ## drat 1.18283 2.48348 0.476 0.6407 ## wt -4.52978 2.53875 -1.784 0.0946 . ## qsec 0.36784 0.93540 0.393 0.6997 ## vs1 1.93085 2.87126 0.672 0.5115 ## am1 1.21212 3.21355 0.377 0.7113 ## gear4 1.11435 3.79952 0.293 0.7733 ## gear5 2.52840 3.73636 0.677 0.5089 ## carb2 -0.97935 2.31797 -0.423 0.6787 ## carb3 2.99964 4.29355 0.699 0.4955 ## carb4 1.09142 4.44962 0.245 0.8096 ## carb6 4.47757 6.38406 0.701 0.4938 ## carb8 7.25041 8.36057 0.867 0.3995 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 2.833 on 15 degrees of freedom ## Multiple R-squared: 0.8931, Adjusted R-squared: 0.779 ## F-statistic: 7.83 on 16 and 15 DF, p-value: 0.000124
R 使用第一个因子水平作为基准组。您需要将其他组的系数与基准组进行比较。
R中的逐步线性回归
本教程的最后一部分是关于逐步回归算法。该算法的目的是添加和删除模型中的潜在候选变量，并保留那些对因变量有显着影响的变量。当数据集包含大量预测变量时，此算法很有意义。您无需手动添加和删除自变量。逐步回归旨在选择最佳候选变量来拟合模型。
让我们实际看看它是如何工作的。为便于教学说明，我们将使用 mtcars 数据集，但仅使用连续变量。在开始分析之前，最好通过相关性矩阵确定数据中的变化。GGally 库是 ggplot2 的扩展。
该库包括不同的函数来显示摘要统计信息，例如矩阵中所有变量的相关性和分布。我们将使用 ggscatmat 函数，但您可以参考文档以获取有关 GGally 库的更多信息。
ggscatmat() 的基本语法是
ggscatmat(df, columns = 1:ncol(df), corMethod = "pearson") arguments: -df: A matrix of continuous variables -columns: Pick up the columns to use in the function. By default, all columns are used -corMethod: Define the function to compute the correlation between variable. By default, the algorithm uses the Pearson formula
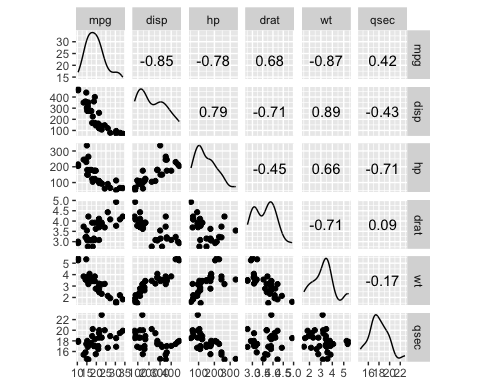
您可以显示所有变量的相关性，并决定哪些变量将是逐步回归第一步的最佳候选变量。您的变量与因变量 mpg 之间存在一些很强的相关性。
library(GGally) df <- mtcars % > % select(-c(am, vs, cyl, gear, carb)) ggscatmat(df, columns = 1: ncol(df))
输出
逐步回归分步示例
变量选择是拟合模型的重要组成部分。逐步回归将自动执行搜索过程。为了估计数据集中有多少可能的选择，您计算
其中 k 是预测变量的数量。随着自变量数量的增加，可能性的数量也会增加。这就是为什么您需要自动搜索。
您需要从 CRAN 安装 olsrr 包。该包尚未在 Anaconda 中提供。因此，您直接从命令行安装它
install.packages("olsrr")
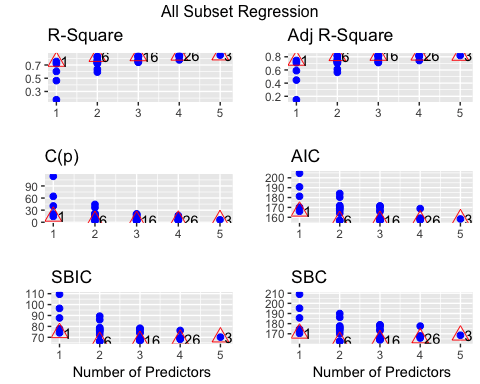
您可以使用拟合标准（例如 R 方、调整后 R 方、贝叶斯标准）绘制所有可能的子集。AIC 标准最低的模型将是最终模型。
library(olsrr) model <- mpg~. fit <- lm(model, df) test <- ols_all_subset(fit) plot(test)
代码解释
- mpg ~.: 构建要估计的模型
- lm(model, df): 运行 OLS 模型
- ols_all_subset(fit): 使用相关统计信息构建图形
- plot(test): 绘制图形
输出
线性回归模型使用t检验来估计自变量对因变量的统计影响。研究人员将最大阈值设定为 10%，较低的值表示更强的统计联系。逐步回归的策略围绕此测试构建，以添加和删除潜在的候选变量。算法工作如下
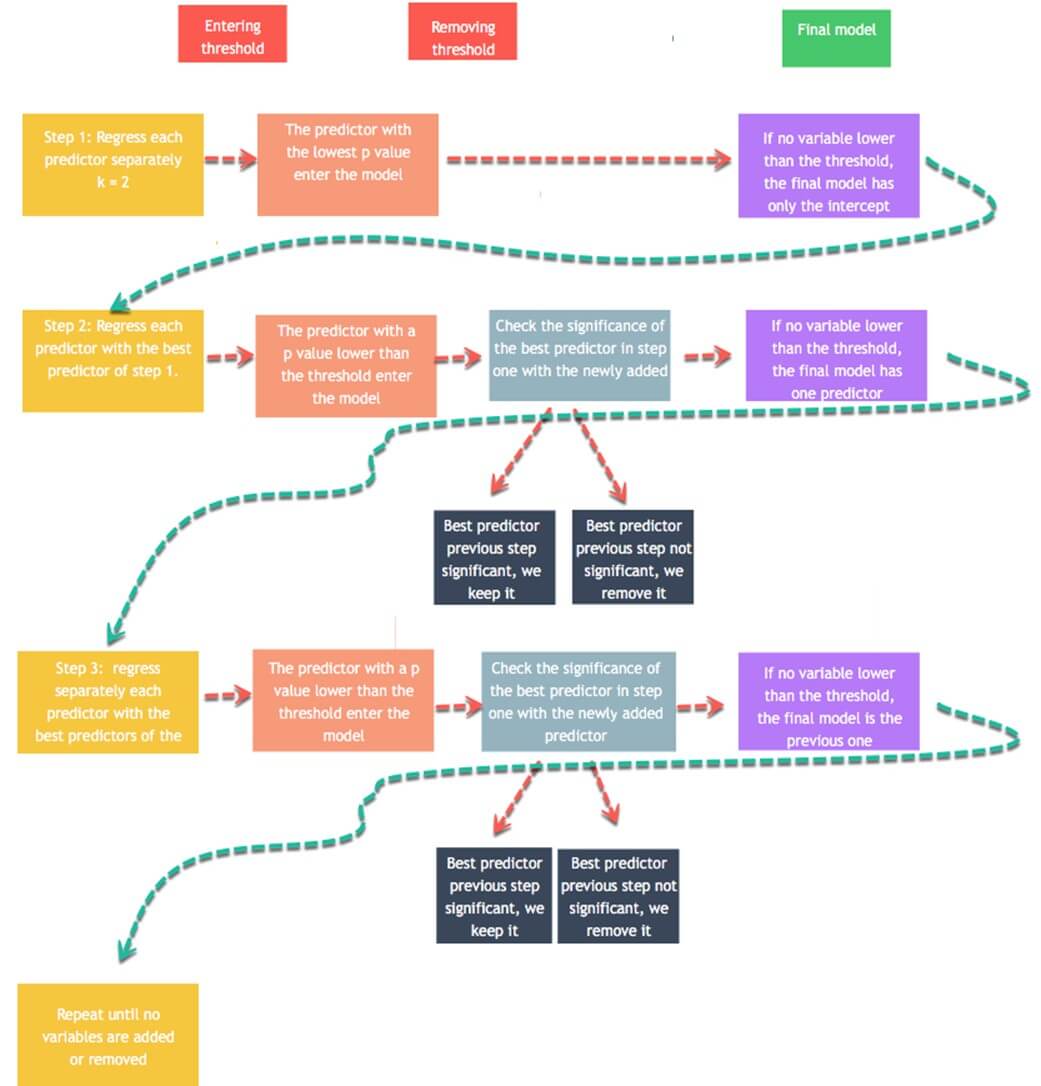
- 步骤 1：分别将每个预测变量回归到 y。即，将 x_1 回归到 y，将 x_2 回归到 y，依此类推，直到 x_n。存储p 值，并保留 p 值低于给定阈值（默认为 0.1）的回归量。显着性低于阈值的预测变量将被添加到最终模型中。如果没有变量的 p 值低于输入阈值，则算法停止，您将获得仅包含常数的最终模型。
- 步骤 2：使用 p 值最低的预测变量，并单独添加一个变量。您回归一个常数、步骤一中最好的预测变量和第三个变量。您将新预测变量添加到逐步模型中，其值低于输入阈值。如果没有变量的 p 值低于 0.1，则算法停止，您将获得仅包含一个预测变量的最终模型。您回归逐步模型以检查第一步最佳预测变量的显着性。如果它高于移除阈值，则将其保留在逐步模型中。否则，将其排除。
- 步骤 3：您对新的最佳逐步模型重复步骤 2。该算法根据输入值向逐步模型添加预测变量，并根据排除阈值排除逐步模型中的预测变量。
- 算法将继续进行，直到没有变量可以添加或排除。
您可以使用 olsrr 包中的 ols_stepwise() 函数来执行该算法。
ols_stepwise(fit, pent = 0.1, prem = 0.3, details = FALSE) arguments: -fit: Model to fit. Need to use `lm()`before to run `ols_stepwise() -pent: Threshold of the p-value used to enter a variable into the stepwise model. By default, 0.1 -prem: Threshold of the p-value used to exclude a variable into the stepwise model. By default, 0.3 -details: Print the details of each step
在此之前，我们向您展示算法的步骤。下表显示了因变量和自变量
| 因变量 | 自变量 |
|---|---|
| mpg | disp |
| hp | |
| drat | |
| wt | |
| qsec |
开始
首先，算法通过分别对每个自变量运行模型来开始。下表显示了每个模型的 p 值。
## [[1]] ## (Intercept) disp ## 3.576586e-21 9.380327e-10 ## ## [[2]] ## (Intercept) hp ## 6.642736e-18 1.787835e-07 ## ## [[3]] ## (Intercept) drat ## 0.1796390847 0.0000177624 ## ## [[4]] ## (Intercept) wt ## 8.241799e-19 1.293959e-10 ## ## [[5] ## (Intercept) qsec ## 0.61385436 0.01708199
要进入模型，算法会保留 p 值最低的变量。从上面的输出可以看出，它是 wt
步骤 1
在第一步中，算法将 mpg 与 wt 以及其他变量独立运行。
## [[1]] ## (Intercept) wt disp ## 4.910746e-16 7.430725e-03 6.361981e-02 ## ## [[2]] ## (Intercept) wt hp ## 2.565459e-20 1.119647e-06 1.451229e-03 ## ## [[3]] ## (Intercept) wt drat ## 2.737824e-04 1.589075e-06 3.308544e-01 ## ## [[4]] ## (Intercept) wt qsec ## 7.650466e-04 2.518948e-11 1.499883e-03
每个变量都是进入最终模型的潜在候选变量。但是，算法只保留 p 值最低的变量。事实证明 hp 的 p 值略低于 qsec。因此，hp 进入最终模型
步骤 2
算法重复第一步，但这次在最终模型中有两个自变量。
## [[1]] ## (Intercept) wt hp disp ## 1.161936e-16 1.330991e-03 1.097103e-02 9.285070e-01 ## ## [[2]] ## (Intercept) wt hp drat ## 5.133678e-05 3.642961e-04 1.178415e-03 1.987554e-01 ## ## [[3]] ## (Intercept) wt hp qsec ## 2.784556e-03 3.217222e-06 2.441762e-01 2.546284e-01
进入最终模型的变量都没有足够的低 p 值。算法在这里停止；我们得到了最终模型
## ## Call: ## lm(formula = mpg ~ wt + hp, data = df) ## ## Residuals: ## Min 1Q Median 3Q Max ## -3.941 -1.600 -0.182 1.050 5.854 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 37.22727 1.59879 23.285 < 2e-16 *** ## wt -3.87783 0.63273 -6.129 1.12e-06 *** ## hp -0.03177 0.00903 -3.519 0.00145 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 2.593 on 29 degrees of freedom ## Multiple R-squared: 0.8268, Adjusted R-squared: 0.8148 ## F-statistic: 69.21 on 2 and 29 DF, p-value: 9.109e-12
您可以使用 ols_stepwise() 函数来比较结果。
stp_s <-ols_stepwise(fit, details=TRUE)
输出
算法在 2 步后找到了解决方案，并返回了与我们之前相同的输出。
最后，您可以说模型由两个变量和一个截距来解释。每加仑英里数与总马力和体重呈负相关
## You are selecting variables based on p value... ## 1 variable(s) added.... ## Variable Selection Procedure ## Dependent Variable: mpg ## ## Stepwise Selection: Step 1 ## ## Variable wt Entered ## ## Model Summary ## -------------------------------------------------------------- ## R 0.868 RMSE 3.046 ## R-Squared 0.753 Coef. Var 15.161 ## Adj. R-Squared 0.745 MSE 9.277 ## Pred R-Squared 0.709 MAE 2.341 ## -------------------------------------------------------------- ## RMSE: Root Mean Square Error ## MSE: Mean Square Error ## MAE: Mean Absolute Error ## ANOVA ## -------------------------------------------------------------------- ## Sum of ## Squares DF Mean Square F Sig. ## -------------------------------------------------------------------- ## Regression 847.725 1 847.725 91.375 0.0000 ## Residual 278.322 30 9.277 ## Total 1126.047 31 ## -------------------------------------------------------------------- ## ## Parameter Estimates ## ---------------------------------------------------------------------------------------- ## model Beta Std. Error Std. Beta t Sig lower upper ## ---------------------------------------------------------------------------------------- ## (Intercept) 37.285 1.878 19.858 0.000 33.450 41.120 ## wt -5.344 0.559 -0.868 -9.559 0.000 -6.486 -4.203 ## ---------------------------------------------------------------------------------------- ## 1 variable(s) added... ## Stepwise Selection: Step 2 ## ## Variable hp Entered ## ## Model Summary ## -------------------------------------------------------------- ## R 0.909 RMSE 2.593 ## R-Squared 0.827 Coef. Var 12.909 ## Adj. R-Squared 0.815 MSE 6.726 ## Pred R-Squared 0.781 MAE 1.901 ## -------------------------------------------------------------- ## RMSE: Root Mean Square Error ## MSE: Mean Square Error ## MAE: Mean Absolute Error ## ANOVA ## -------------------------------------------------------------------- ## Sum of ## Squares DF Mean Square F Sig. ## -------------------------------------------------------------------- ## Regression 930.999 2 465.500 69.211 0.0000 ## Residual 195.048 29 6.726 ## Total 1126.047 31 ## -------------------------------------------------------------------- ## ## Parameter Estimates ## ---------------------------------------------------------------------------------------- ## model Beta Std. Error Std. Beta t Sig lower upper ## ---------------------------------------------------------------------------------------- ## (Intercept) 37.227 1.599 23.285 0.000 33.957 40.497 ## wt -3.878 0.633 -0.630 -6.129 0.000 -5.172 -2.584 ## hp -0.032 0.009 -0.361 -3.519 0.001 -0.050 -0.013 ## ---------------------------------------------------------------------------------------- ## No more variables to be added or removed.
机器学习
机器学习在数据科学家中越来越普及，并在您日常使用的数百种产品中得到应用。最早的 ML 应用之一是垃圾邮件过滤器。
以下是机器学习的其他应用-
- 识别电子邮件中不必要的垃圾邮件
- 细分客户行为以进行有针对性的广告
- 减少欺诈性信用卡交易
- 优化家庭和办公楼的能源使用
- 面部识别
监督学习
在监督学习中，您提供给算法的训练数据包含一个标签。
分类可能是最常用的监督学习技术。研究人员最早处理的分类任务之一就是垃圾邮件过滤器。学习的目标是预测电子邮件是归类为垃圾邮件还是正常邮件。机器在训练步骤之后，可以检测电子邮件的类别。
回归通常用于机器学习领域来预测连续值。回归任务可以根据一组自变量（也称为预测变量或回归量）来预测因变量的值。例如，线性回归可以预测股票价格、天气预报、销售额等。
以下是一些基本的监督学习算法列表。
- 线性回归
- 逻辑回归
- 最近邻
- 支持向量机 (SVM)
- 决策树和随机森林
- 神经网络
无监督学习
在无监督学习中，训练数据是无标签的。系统在没有参考的情况下尝试学习。以下是无监督学习算法的列表。
- K-均值
- 层次聚类分析
- 期望最大化
- 可视化和降维
- 主成分分析
- 核 PCA
- 局部线性嵌入
摘要
- 线性回归回答了一个简单的问题：你能衡量一个目标变量和一个预测变量集之间的确切关系吗？
- 最小二乘法尝试查找最小化误差平方和的参数，即预测的 y 值与实际的 y 值之间的垂直距离。
- 包含一个以上自变量的概率模型称为多元回归模型。
- 逐步线性回归算法的目的是添加和删除模型中的潜在候选变量，并保留那些对因变量有显着影响的变量。
- 变量选择是拟合模型的重要组成部分。逐步回归自动执行搜索过程。
普通最小二乘回归可以总结在下表中
| 库 | 目标 | 函数 | 参数 |
|---|---|---|---|
| base | 计算线性回归 | lm() | formula, data |
| base | 总结模型 | summarize() | fit |
| base | 提取系数 | lm()$coefficient | |
| base | 提取残差 | lm()$residuals | |
| base | 提取拟合值 | lm()$fitted.values | |
| olsrr | 运行逐步回归 | ols_stepwise() | fit, pent = 0.1, prem = 0.3, details = FALSE |
注意：请记住在拟合模型之前将分类变量转换为因子。
