R 方差分析教程：单因素与双因素（含示例）

作者： Evelyn Clarke Evelyn Clarke
小时 - 权威教程 更新于

什么是方差分析？

方差分析（ANOVA）是一种统计技术，通常用于研究两个或多个组均值之间的差异。方差分析检验的核心在于一个典型变量中不同变异来源。R中的方差分析主要提供组间均值相等的证据。这种统计方法是t检验的扩展。它适用于因子变量有多个组的情况。

单因素方差分析

在许多情况下，您需要比较多个组之间的均值。例如，营销部门想知道三个团队是否具有相同的销售业绩。

  • 团队：3个水平的因子：A、B和C
  • 销售：业绩衡量指标

方差分析检验可以告诉您这三个组的业绩是否相似。

为了弄清楚数据是否来自同一总体，您可以进行单因素方差分析（以下简称单因素方差分析）。该检验与任何其他统计检验一样，提供了关于是否可以接受或拒绝H0假设的证据。

单因素方差分析检验中的假设

  • H0：组间均值相同
  • H3：至少一个组的均值不同

换句话说，H0假设意味着没有足够的证据证明（因子）的组均值与其他组不同。

此检验类似于t检验，尽管在2个以上组的情况下建议使用方差分析检验。除此之外，t检验和方差分析提供相似的结果。

假设

我们假设每个因子都是随机抽样的，是独立的，并且来自具有未知但相等方差的正态分布总体。

解释方差分析检验

F统计量用于检验数据是否来自显著不同的总体，即不同的样本均值。

要计算F统计量，您需要将组间变异除以组内变异。

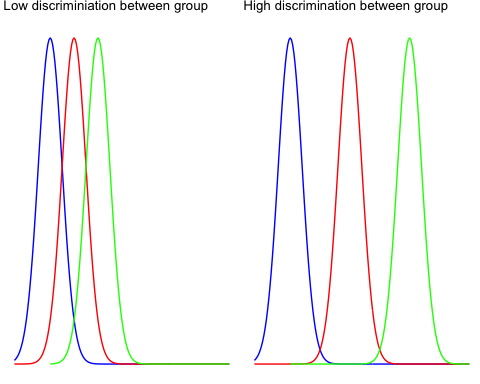
组间变异反映了所有总体中组与组之间的差异。查看下面的两个图以理解组间方差的概念。

左图显示三个组之间的变异非常小，并且三个均值很可能趋于总体均值（即三个组的均值）。

右图绘制了三个相距很远的分布，并且它们没有重叠。总体均值与组均值之间的差异很大的可能性很高。

Interpret ANOVA test

组内变异考虑了组与组之间的差异。变异来自个体观测值；有些点可能与组均值完全不同。组内变异反映了这种效应，并指抽样误差。

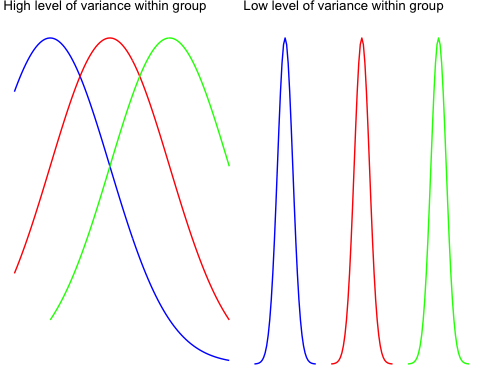
为了在视觉上理解组内变异的概念，请看下图。

左侧图显示了三个不同组的分布。您增加了每个样本的散布，并且很明显个体方差很大。F检验将减小，这意味着您倾向于接受零假设。

右侧图显示了完全相同的样本（均值相同），但变异性较低。这会导致F检验增加，并倾向于支持备择假设。

Interpret ANOVA test

您可以使用这两种度量来构建F统计量。理解F统计量非常直观。如果分子增加，则意味着组间变异性很大，并且样本中的组很可能来自完全不同的分布。

换句话说，较低的F统计量表示组平均值之间几乎没有或没有显著差异。

单因素方差分析检验示例

您将使用poison数据集来实现单因素方差分析检验。该数据集包含48行和3个变量

  • Time：动物的生存时间
  • poison：使用的毒药类型：因子水平：1、2和3
  • treat：使用的治疗类型：因子水平：1、2和3

在开始计算方差分析检验之前，您需要按照以下步骤准备数据

  • 步骤1: 导入数据
  • 步骤2：删除不必要的变量
  • 步骤3：将poison变量转换为有序级别
library(dplyr)
PATH <- "https://raw.githubusercontent.com/guru99-edu/R-Programming/master/poisons.csv"
df <- read.csv(PATH) %>%
select(-X) %>% 
mutate(poison = factor(poison, ordered = TRUE))
glimpse(df)

输出

## Observations: 48
## Variables: 3
## $ time   <dbl> 0.31, 0.45, 0.46, 0.43, 0.36, 0.29, 0.40, 0.23, 0.22, 0...
## $ poison <ord> 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 1, 1, 1, 1, 2, 2, 2...
## $ treat  <fctr> A, A, A, A, A, A, A, A, A, A, A, A, B, B, B, B, B, B, ...

我们的目标是检验以下假设

  • H0：组间生存时间平均值无差异
  • H3：至少有一个组的生存时间平均值不同。

换句话说，您想知道根据给予豚鼠的毒药类型，生存时间均值之间是否存在统计学上的差异。

您将按以下步骤进行

  • 步骤1：检查poison变量的格式
  • 步骤2：打印摘要统计信息：计数、均值和标准差
  • 步骤3：绘制箱形图
  • 步骤4：计算单因素方差分析检验
  • 步骤5：运行成对t检验

步骤1）您可以使用以下代码检查poison的级别。您应该会看到三个字符值，因为您使用mutate动词将它们转换为因子。

levels(df$poison)

输出

## [1] "1" "2" "3"

步骤2）您计算均值和标准差。

df % > %
	group_by(poison) % > %
	summarise(
		count_poison = n(),
		mean_time = mean(time, na.rm = TRUE),
		sd_time = sd(time, na.rm = TRUE)
	)

输出

## 
# A tibble: 3 x 4
##   poison count_poison mean_time    sd_time
##    <ord>        <int>     <dbl>      <dbl>
## 1      1           16  0.617500 0.20942779
## 2      2           16  0.544375 0.28936641
## 3      3           16  0.276250 0.06227627

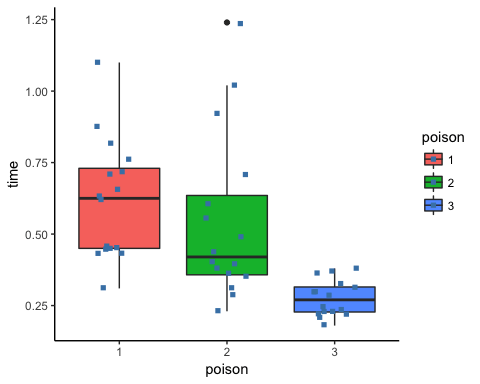
步骤3）在第三步中，您可以以图形方式检查分布之间是否存在差异。请注意，您包含了一个抖动的点。

ggplot(df, aes(x = poison, y = time, fill = poison)) +
    geom_boxplot() +
    geom_jitter(shape = 15,
        color = "steelblue",
        position = position_jitter(0.21)) +
    theme_classic()

输出

One way ANOVA Test Example

步骤4）您可以使用aov命令运行单因素方差分析检验。方差分析检验的基本语法是

相关文章

aov(formula, data)
Arguments:			
- formula: The equation you want to estimate
- data: The dataset used

公式的语法是

y ~ X1+ X2+...+Xn # X1 +  X2 +... refers to the independent variables
y ~ . # use all the remaining variables as independent variables

您就可以回答我们的问题：在已知给予的毒药类型的情况下，豚鼠的生存时间之间是否存在任何差异。

请注意，建议存储模型并使用summary()函数以更好地打印结果。

anova_one_way <- aov(time~poison, data = df)
summary(anova_one_way)

代码解释

  • aov(time ~ poison, data = df)：使用以下公式运行方差分析检验
  • summary(anova_one_way)：打印检验摘要

输出

##             Df Sum Sq Mean Sq F value   Pr(>F)
## poison       2  1.033  0.5165   11.79 7.66e-05 ***
## Residuals   45  1.972  0.0438                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

p值低于通常的0.05阈值。您可以肯定地说，组之间存在统计学上的差异，如“*”所示。

成对比较

单因素方差分析检验不告知哪个组的均值不同。相反，您可以使用TukeyHSD()函数执行Tukey检验。

TukeyHSD(anova_one_way)

输出

Pairwise comparison

双因素方差分析

双因素方差分析在公式中添加了另一个组变量。它与单因素方差分析相同，尽管公式略有不同

y=x1+x2

其中y是定量变量，x1和x2是分类变量。

双因素方差分析检验中的假设

  • H0：两个变量（即因子变量）的均值相等
  • H3：两个变量的均值不同

您将treat变量添加到我们的模型中。此变量指示给予豚鼠的治疗。您有兴趣了解毒药和给予豚鼠的治疗之间是否存在统计学上的依赖性。

我们通过添加treat和另一个自变量来调整代码。

anova_two_way <- aov(time~poison + treat, data = df)
summary(anova_two_way)

输出

##             Df Sum Sq Mean Sq F value  Pr(>F)    
## poison       2 1.0330  0.5165   20.64 5.7e-07 ***
## treat        3 0.9212  0.3071   12.27 6.7e-06 ***
## Residuals   42 1.0509  0.0250                    
## ---

您可以得出结论，poison和treat都与0在统计学上存在显著差异。您可以拒绝零假设，并确认改变治疗或毒药会影响生存时间。

摘要

我们可以在下表中总结检验结果

测试 代码 假设 P值
单因素方差分析 
aov(y ~ X, data = df)
 H3：至少有一个组的平均值不同 0.05
成对 
TukeyHSD(ANOVA summary)
 0.05
双因素方差分析 
aov(y ~ X1 + X2, data = df)
 H3：两个组的平均值都不同 0.05