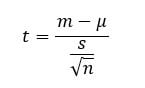R编程中的T检验:单样本和配对T检验[示例]
什么是统计推断?
统计推断是关于数据分布生成结论的艺术。数据科学家经常会遇到只能通过科学方法回答的问题。因此,统计推断是一种检验假设是否成立,即是否由数据验证的策略。
评估假设的常用策略是进行t检验。t检验可以判断两组之间是否存在相同的均值。t检验也称为学生t检验。t检验可以估计
- 单个向量(即单样本t检验)
- 来自同一样本组的两个向量(即配对t检验)。
您假设这两个向量都是随机抽取的、独立的,并且来自具有未知但相等方差的正态分布总体。
R语言中的T检验是什么?
T检验的基本思想是使用统计学来评估两个相反的假设
- H0:零假设:均值与所用样本相同
- H3:真实假设:均值与所用样本不同
T检验常用于小样本量。要进行t检验,您需要假设数据服从正态分布。
R中的T检验语法
R中t.test()的基本语法是
t.test(x, y = NULL,
mu = 0, var.equal = FALSE)
arguments:
- x : A vector to compute the one-sample t-test
- y: A second vector to compute the two sample t-test
- mu: Mean of the population- var.equal: Specify if the variance of the two vectors are equal. By default, set to `FALSE`
R中的单样本t检验
单样本t检验,或称学生t检验,将一个向量的均值与理论均值进行比较,计算t检验的公式是
此处,
指的是均值
指理论均值
- s是标准差
- n是观察次数。
要评估t检验的统计显著性,您需要计算p值。p值的范围是0到1,其解释如下
- p值小于0.05意味着您非常有信心拒绝零假设,因此接受H3。
- p值大于0.05表明您没有足够的证据拒绝零假设。
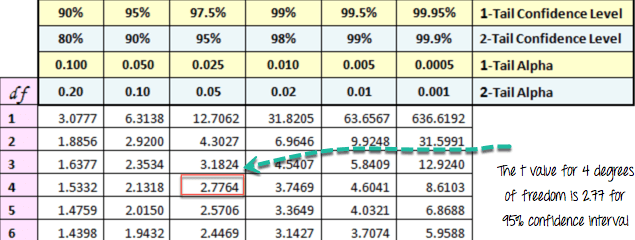
通过查看t检验的相应绝对值在自由度等于的学生分布中的值,您可以构建p值
例如,如果您有5次观察,您需要将t值与学生分布中自由度为4且置信度为95%的值进行比较。要拒绝零假设,t值应大于2.77。
请参见下表
R中的单样本t检验示例
假设您是一家生产饼干的公司。每块饼干应该含有10克糖。饼干由一台机器生产,该机器在混合所有东西之前将糖添加到碗中。您认为机器并没有为每块饼干添加10克糖。如果您的假设为真,则需要修理机器。您存储了三十块饼干的糖分含量。
注意:您可以使用rnorm()函数创建一个随机向量。此函数生成正态分布的值。基本语法是
rnorm(n, mean, sd) arguments - n: Number of observations to generate - mean: The mean of the distribution. Optional - sd: The standard deviation of the distribution. Optional
您可以使用30个观察值创建一个均值为9.99,标准差为0.04的分布。
set.seed(123) sugar_cookie <- rnorm(30, mean = 9.99, sd = 0.04) head(sugar_cookie)
输出
## [1] 9.967581 9.980793 10.052348 9.992820 9.995172 10.058603
您可以使用单样本t检验来检查糖分含量是否与配方不同。您可以进行假设检验
- H0:平均糖分含量等于10
- H3:平均糖分含量不等于10
您使用0.05的显著性水平。
# H0 : mu = 10 t.test(sugar_cookie, mu = 10)
这是输出
单样本t检验的p值为0.1079,大于0.05。您可以确信95%的机器添加的糖量在9.973克到10.002克之间。您不能拒绝零(H0)假设。没有足够的证据表明机器添加的糖量不符合配方。
R中的配对t检验
配对t检验,或称依赖样本t检验,用于当处理组的均值被计算两次时。配对t检验的基本应用是
- A/B测试:比较两个变体
- 病例对照研究:治疗前后
R中的配对t检验示例
一家饮料公司对促销计划对销售的影响感兴趣。该公司决定跟踪其一家商店的日常销售情况,在该商店推广该计划。计划结束后,该公司希望了解商店的平均销售额在该计划前后是否存在统计学上的差异。
- 该公司在计划开始前的每一天都跟踪了销售情况。这是我们的第一个向量。
- 该计划推广了一周,并且每天都记录销售情况。这是我们的第二个向量。
- 您将执行t检验来判断该计划的有效性。这被称为配对t检验,因为两个向量的值来自相同的分布(即同一家商店)。
假设检验是
- H0:均值无差异
- H3:两个均值不同
请记住,t检验的一个假设是未知但相等的方差。实际上,数据很少具有相等的均值,这会导致t检验结果不正确。
放宽相等方差假设的一个解决方案是使用Welch检验。R默认假定这两个方差不相等。在您的数据集中,两个向量具有相同的方差,您可以设置var.equal= TRUE。
您创建了两个来自高斯分布的随机向量,在促销计划之后的销售均值更高。
set.seed(123) # sales before the program sales_before <- rnorm(7, mean = 50000, sd = 50) # sales after the program.This has higher mean sales_after <- rnorm(7, mean = 50075, sd = 50) # draw the distribution t.test(sales_before, sales_after,var.equal = TRUE)
您获得的p值为0.04606,低于0.05的阈值。您得出结论,两组的均值存在显著差异。该计划提高了商店的销售额。
摘要
- 统计推断是关于数据分布生成结论的艺术。
- T检验属于推断统计学。它通常用于确定两组均值之间是否存在统计学上的差异。
- 单样本t检验,或称学生t检验,将向量的均值与理论均值进行比较。
- 配对t检验,或称依赖样本t检验,用于当处理组的均值被计算两次时。
我们可以总结t检验如下表所示
| 测试 | 要检验的假设 | p值 | 代码 | 可选参数 |
|---|---|---|---|---|
| 单样本t检验 | 向量的均值与理论均值不同 | 0.05 |
t.test(x, mu = mean) |
|
| 配对样本t检验 | 同一组的均值A与均值B不同 | 0.06 |
t.test(A,B, mu = mean) |
var.equal= TRUE |
如果我们假设方差相等,则需要更改参数var.equal= TRUE。