RNN(循环神经网络)教程:TensorFlow 示例
为什么我们需要循环神经网络 (RNN)?
循环神经网络 (RNN) 允许您构建记忆单元来持续存储数据并模拟短期依赖关系。它还用于时间序列预测,以识别数据相关性和模式。它通过提供与人脑相似的行为来帮助为序列数据生成预测结果。
人工神经网络的结构相对简单,主要涉及矩阵乘法。在第一步中,输入乘以初始随机权重和偏置,通过激活函数进行转换,然后输出值用于进行预测。这一步可以了解网络与现实之间的差距。
应用的度量是损失。损失函数越高,模型越“笨”。为了提高网络的知识,需要通过调整网络权重来进行优化。随机梯度下降是用于将权重值朝着正确方向改变的方法。一旦做出调整,网络就可以使用另一批数据来测试其新知识。
幸运的是,错误比之前低了,但仍然不够小。优化步骤会迭代进行,直到错误最小化,即无法再提取更多信息。
这种模型的缺点是它没有任何记忆。这意味着输入和输出是独立的。换句话说,模型不关心之前发生了什么。当您需要预测时间序列或句子时,这会引发一些问题,因为网络需要有关历史数据或过去单词的信息。
为了克服这个问题,一种新的架构被开发出来:循环神经网络 (以下简称 RNN)
什么是循环神经网络 (RNN)?
循环神经网络 (RNN) 是一类人工神经网络,其中不同节点之间的连接形成一个有向图,以产生时间动态行为。它有助于模拟从前馈网络派生的序列数据。它的工作方式类似于人脑,可以提供预测结果。
循环神经网络看起来与传统神经网络非常相似,只是在神经元中添加了记忆状态。包含记忆的计算很简单。
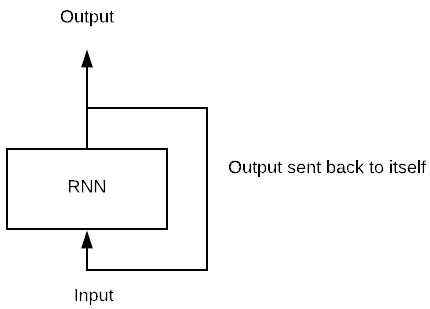
想象一个只有一个神经元的简单模型,它由一批数据输入。在传统的神经网络中,模型通过将输入乘以权重和激活函数来产生输出。在 RNN 中,此输出会反复地反馈给自己。我们称输出成为下一个矩阵乘法输入的时间步。
例如,在下面的图片中,您可以看到网络由一个神经元组成。网络计算输入和权重之间的矩阵乘法,并通过激活函数添加非线性。它成为 t-1 时刻的输出。此输出是第二次矩阵乘法的输入。
下面,我们用 TensorFlow 编写一个简单的 RNN 来理解步骤以及输出的形状。
网络由以下部分组成:
- 四个输入
- 六个神经元
- 2 个时间步
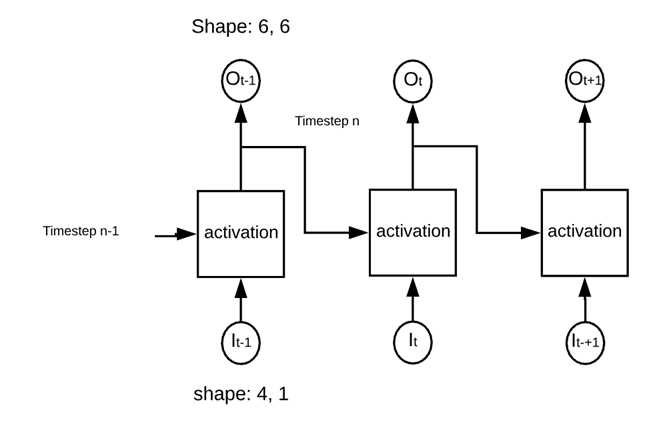
网络将按以下图片所示进行。
该网络之所以称为“循环”,是因为它在每个激活的正方形中执行相同的操作。网络在应用激活函数之前计算输入和先前输出的权重。
import numpy as np
import tensorflow as tf
n_inputs = 4
n_neurons = 6
n_timesteps = 2
The data is a sequence of a number from 0 to 9 and divided into three batches of data.
## Data
X_batch = np.array([
[[0, 1, 2, 5], [9, 8, 7, 4]], # Batch 1
[[3, 4, 5, 2], [0, 0, 0, 0]], # Batch 2
[[6, 7, 8, 5], [6, 5, 4, 2]], # Batch 3
])
我们可以通过占位符来构建网络,用于数据、循环阶段和输出。
- 定义数据占位符
X = tf.placeholder(tf.float32, [None, n_timesteps, n_inputs])
这里
- None:未知,将取批次的大小
- n_timesteps:网络将输出反馈给神经元的次数
- n_inputs:每批的输入数量
- 定义循环网络
如上图所示,网络由 6 个神经元组成。网络将计算两个点积:
- 输入数据与第一组权重(即 6:等于神经元数量)
- 先前输出与第二组权重(即 6:对应于输出数量)
请注意,在第一次前向传播期间,先前输出的值等于零,因为我们没有任何可用值。
构建 RNN 的对象是 tf.contrib.rnn.BasicRNNCell,参数 num_units 用于定义输入的数量。
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
现在网络已定义,您可以计算输出和状态。
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
此对象使用内部循环将矩阵乘以适当的次数。
请注意,循环神经元是先前时间步所有输入的函数。这就是网络构建自身记忆的方式。来自先前时间的信息可以传播到未来时间。这就是循环神经网络的神奇之处。
## Define the shape of the tensor
X = tf.placeholder(tf.float32, [None, n_timesteps, n_inputs])
## Define the network
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
init = tf.global_variables_initializer()
init = tf.global_variables_initializer()
with tf.Session() as sess:
init.run()
outputs_val = outputs.eval(feed_dict={X: X_batch})
print(states.eval(feed_dict={X: X_batch}))
[[ 0.38941205 -0.9980438 0.99750966 0.7892596 0.9978241 0.9999997 ]
[ 0.61096436 0.7255889 0.82977575 -0.88226104 0.29261455 -0.15597084]
[ 0.62091285 -0.87023467 0.99729395 -0.58261937 0.9811445 0.99969864]]
为了便于解释,您可以打印先前状态的值。上面打印的输出显示了来自最后一个状态的输出。现在打印所有输出,您会注意到状态是每个批次的先前输出。也就是说,先前输出包含有关整个序列的信息。
print(outputs_val)
print(outputs_val.shape)
[[[-0.75934666 -0.99537754 0.9735819 -0.9722234 -0.14234993
-0.9984044 ]
[ 0.99975264 -0.9983206 0.9999993 -1. -0.9997506
-1. ]]
[[ 0.97486496 -0.98773265 0.9969686 -0.99950117 -0.7092863
-0.99998885]
[ 0.9326837 0.2673438 0.2808514 -0.7535883 -0.43337247
0.5700631 ]]
[[ 0.99628735 -0.9998728 0.99999213 -0.99999976 -0.9884324
-1. ]
[ 0.99962527 -0.9467421 0.9997403 -0.99999714 -0.99929446
-0.9999795 ]]]
(3, 2, 6)
输出的形状为 (3, 2, 6)
- 3:批次数
- 2:时间步数
- 6:神经元数量
循环神经网络的优化与传统神经网络相同。您将在下一部分循环神经网络教程中更详细地了解如何编写优化。
RNN 的应用
RNN 有多种用途,尤其是在预测未来方面。在金融行业,RNN 可以帮助预测股票价格或股市方向的信号(即正面或负面)。
RNN 对自动驾驶汽车很有用,因为它可以通过预测车辆轨迹来避免车祸。
RNN 广泛用于文本分析、图像字幕、情感分析和机器翻译。例如,可以使用电影评论来理解观众在观看电影后所感知的情绪。当电影公司没有足够的时间审查、标记、整合和分析评论时,自动化这项任务非常有用。机器可以以更高的准确性完成这项工作。
RNN 的局限性
理论上,RNN 应该能将信息传递到很长的时间。然而,当时间步太长时,传播所有这些信息是相当具有挑战性的。当网络有很多深度层时,它会变得难以训练。这个问题称为:梯度消失问题。如果您还记得,神经网络使用梯度下降算法更新权重。当网络向下推进到较低层时,梯度会变小。
总之,梯度保持不变,意味着没有改进的空间。模型从梯度的变化中学习;这种变化会影响网络的输出。然而,如果梯度差异太小(即权重变化很小),网络就无法学习任何东西,输出也无法学习。因此,面临梯度消失问题的网络无法收敛到好的解决方案。
LSTM 改进
为了克服 RNN 面临的潜在梯度消失问题,三位研究人员 Hochreiter、Schmidhuber 和 Bengio 通过一种称为长短期记忆 (LSTM) 的架构改进了 RNN。简而言之,LSTM 为网络提供相关的过去信息给最近的时间。机器使用更好的架构来选择和携带信息到稍后的时间。
LSTM 架构在 TensorFlow 中可用,即 tf.contrib.rnn.LSTMCell。LSTM 超出了本教程的范围。您可以参考官方文档以获取更多信息。
时间序列中的 RNN
在本 TensorFlow RNN 教程中,您将使用具有时间序列数据的 RNN。时间序列依赖于过去,这意味着过去的值包含网络可以从中学习的相关信息。时间序列预测背后的思想是估计一个序列的未来值,例如股票价格、温度、GDP 等。
Keras RNN 和时间序列的数据准备可能有点棘手。首先,目标是预测序列的下一个值,这意味着您将使用过去的信息来估计 t + 1 时刻的值。标签等于输入序列,并提前一个周期移位。其次,输入数量设置为 1,即每个时间只有一个观测值。最后,时间步等于数值序列。例如,如果您将时间步设置为 10,输入序列将返回连续十次。
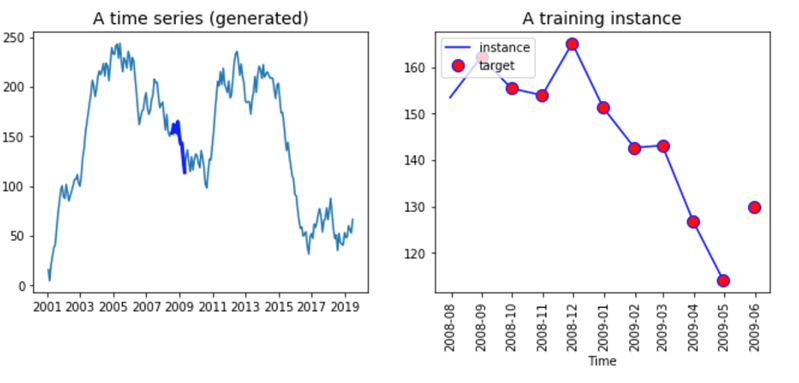
看看下面的图表,我们在左边表示了时间序列数据,在右边表示了一个虚构的输入序列。您创建一个函数来返回一个数据集,其中包含 2001 年 1 月至 2016 年 12 月的随机值。
# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
def create_ts(start = '2001', n = 201, freq = 'M'):
rng = pd.date_range(start=start, periods=n, freq=freq)
ts = pd.Series(np.random.uniform(-18, 18, size=len(rng)), rng).cumsum()
return ts
ts= create_ts(start = '2001', n = 192, freq = 'M')
ts.tail(5)
输出
2016-08-31 -93.459631 2016-09-30 -95.264791 2016-10-31 -95.551935 2016-11-30 -105.879611 2016-12-31 -123.729319 Freq: M, dtype: float64
ts = create_ts(start = '2001', n = 222)
# Left
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.plot(ts.index, ts)
plt.plot(ts.index[90:100], ts[90:100], "b-", linewidth=3, label="A training instance")
plt.title("A time series (generated)", fontsize=14)
# Right
plt.subplot(122)
plt.title("A training instance", fontsize=14)
plt.plot(ts.index[90:100], ts[90:100], "b-", markersize=8, label="instance")
plt.plot(ts.index[91:101], ts[91:101], "bo", markersize=10, label="target", markerfacecolor='red')
plt.legend(loc="upper left")
plt.xlabel("Time")
plt.show()
图表的右侧显示了所有序列。它始于 2001 年,结束于 2019 年。将所有数据输入网络是没有意义的,相反,您需要创建一个长度等于时间步的批次数据。这个批次将是 X 变量。Y 变量与 X 相同,但移位一个周期(即,您想预测 t+1)。
两个向量具有相同的长度。您可以在上图的右侧看到它。线条代表 X 输入的十个值,而红点是标签 Y 的十个值。请注意,标签比 X 提前一个周期开始,并在之后一个周期结束。
使用 TensorFlow 构建 RNN 来预测时间序列
现在,在这次 RNN 训练中,是时候构建您的第一个 RNN 来预测上述序列了。您需要为模型指定一些超参数(模型的参数,即神经元数量等)。
- 输入数量:1
- 时间步(时间序列中的窗口):10
- 神经元数量:120
- 输出数量:1
您的网络将从一个 10 天的序列中学习,并包含 120 个循环神经元。您输入模型一个输入,即一天。随时可以更改这些值,看看模型是否有所改进。
在构建模型之前,您需要将数据集分割成训练集和测试集。整个数据集有 222 个数据点;您将使用前 201 个点来训练模型,最后 21 个点来测试您的模型。
定义训练集和测试集后,您需要创建一个包含批次的对象。在这些批次中,您有 X 值和 Y 值。记住 X 值滞后一个周期。因此,您使用前 200 个观测值,时间步等于 10。X_batches 对象应包含 20 个批次,大小为 10*1。y_batches 的形状与 X_batches 对象相同,但提前一个周期。
步骤 1) 创建训练集和测试集
首先,您将序列转换为 numpy 数组;然后,您定义窗口(即网络将从中学习的时间数)、输入数量、输出数量以及训练集的大小,如下面的 TensorFlow RNN 示例所示。
series = np.array(ts) n_windows = 20 n_input = 1 n_output = 1 size_train = 201
之后,您只需将数组分割成两个数据集。
## Split data train = series[:size_train] test = series[size_train:] print(train.shape, test.shape) (201,) (21,)
步骤 2) 创建返回 X_batches 和 y_batches 的函数
为了方便起见,您可以创建一个函数,该函数返回两个不同的数组,一个用于 X_batches,一个用于 y_batches。
让我们编写一个 RNN TensorFlow 函数来构建批次。
请注意,X 批次会滞后一个周期(我们取值 t-1)。函数输出应具有三个维度。第一个维度等于批次数,第二个维度等于窗口大小,第三个维度等于输入数量。
棘手的部分是正确选择数据点。对于 X 数据点,您选择从 t = 1 到 t = 200 的观测值,而对于 Y 数据点,您返回从 t = 2 到 201 的观测值。一旦您获得了正确的数据点,重塑序列就很容易了。
要构造带有批次的对象,您需要将数据集分割成十个等长的批次(即 20 个)。您可以使用 reshape 方法并传递 -1,以便序列与批次大小相似。值 20 是每批的观测数量,1 是输入数量。
您需要对标签执行相同的步骤。
请注意,您需要将数据移位您想要预测的次数。例如,如果您想预测一个周期,那么您将序列移位 1。如果您想预测两天,那么将数据移位 2。
x_data = train[:size_train-1]: Select all the training instance minus one day
X_batches = x_data.reshape(-1, windows, input): create the right shape for the batch e.g (10, 20, 1)
def create_batches(df, windows, input, output):
## Create X
x_data = train[:size_train-1] # Select the data
X_batches = x_data.reshape(-1, windows, input) # Reshape the data
## Create y
y_data = train[n_output:size_train]
y_batches = y_data.reshape(-1, windows, output)
return X_batches, y_batches
现在函数已定义,您可以按照下面的 RNN 示例所示调用它来创建批次。
X_batches, y_batches = create_batches(df = train,
windows = n_windows,
input = n_input,
output = n_output)
您可以打印形状以确保维度正确。
print(X_batches.shape, y_batches.shape) (10, 20, 1) (10, 20, 1)
您需要创建只有一批数据和 20 个观测值的测试集。
请注意,您是逐日预测的,这意味着第二个预测值将基于测试数据集中第一天 (t+1) 的真实值。事实上,真实值将是已知的。
如果您想预测 t+2(即提前两天),您需要使用预测值 t+1;如果您想预测 t+3(提前三天),您需要使用预测值 t+1 和 t+2。因此,准确预测 t+n 天是困难的,这是有道理的。
X_test, y_test = create_batches(df = test, windows = 20,input = 1, output = 1) print(X_test.shape, y_test.shape) (10, 20, 1) (10, 20, 1)
好了,您的批次大小已准备就绪,您可以构建 RNN 架构了。请记住,您有 120 个循环神经元。
步骤 3) 构建模型
要创建模型,您需要定义三个部分:
- 带有张量的变量
- RNN
- 损失和优化
步骤 3.1) 变量
您需要指定具有适当形状的 X 和 y 变量。这一步很简单。张量的维度与 X_batches 和 y_batches 对象相同。
例如,张量 X 是一个占位符(请参阅关于 TensorFlow 简介的教程,以回顾变量声明),它有三个维度:
- 注意:批次大小
- n_windows:窗口的长度。即模型向后看的时间数。
- n_input:输入数量
结果是
tf.placeholder(tf.float32, [None, n_windows, n_input])
## 1. Construct the tensors X = tf.placeholder(tf.float32, [None, n_windows, n_input]) y = tf.placeholder(tf.float32, [None, n_windows, n_output])
步骤 3.2) 创建 RNN
在本 RNN TensorFlow 示例的第二部分,您需要定义网络的架构。与之前一样,您将使用 TensorFlow estimator 的 BasicRNNCell 和 dynamic_rnn 对象。
## 2. create the model basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=r_neuron, activation=tf.nn.relu) rnn_output, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
下一部分有点棘手,但可以加快计算速度。您需要将运行输出转换为密集层,然后再次将其转换以使其维度与输入相同。
stacked_rnn_output = tf.reshape(rnn_output, [-1, r_neuron]) stacked_outputs = tf.layers.dense(stacked_rnn_output, n_output) outputs = tf.reshape(stacked_outputs, [-1, n_windows, n_output])
步骤 3.3) 创建损失和优化
模型优化取决于您正在执行的任务。在之前的 CNN 教程中,您的目标是对图像进行分类,而在本 RNN 教程中,目标略有不同。您被要求对连续变量进行预测,而不是类别。
这个区别很重要,因为它会改变优化问题。连续变量的优化问题是最小化均方误差。要在 TF 中构建这些指标,您可以使用:
- tf.reduce_sum(tf.square(outputs – y))
RNN 代码的其余部分与之前相同,您使用 Adam 优化器来减小损失(即 MSE)。
- tf.train.AdamOptimizer(learning_rate=learning_rate)
- optimizer.minimize(loss)
就是这样,您可以将所有内容打包在一起,您的模型就可以开始训练了。
tf.reset_default_graph() r_neuron = 120 ## 1. Construct the tensors X = tf.placeholder(tf.float32, [None, n_windows, n_input]) y = tf.placeholder(tf.float32, [None, n_windows, n_output]) ## 2. create the model basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=r_neuron, activation=tf.nn.relu) rnn_output, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32) stacked_rnn_output = tf.reshape(rnn_output, [-1, r_neuron]) stacked_outputs = tf.layers.dense(stacked_rnn_output, n_output) outputs = tf.reshape(stacked_outputs, [-1, n_windows, n_output]) ## 3. Loss + optimization learning_rate = 0.001 loss = tf.reduce_sum(tf.square(outputs - y)) optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(loss) init = tf.global_variables_initializer()
您将使用 1500 个 epoch 训练模型,并每 150 次迭代打印一次损失。模型训练完成后,您将在测试集上评估模型,并创建一个包含预测的对象,如下面的循环神经网络示例所示。
iteration = 1500
with tf.Session() as sess:
init.run()
for iters in range(iteration):
sess.run(training_op, feed_dict={X: X_batches, y: y_batches})
if iters % 150 == 0:
mse = loss.eval(feed_dict={X: X_batches, y: y_batches})
print(iters, "\tMSE:", mse)
y_pred = sess.run(outputs, feed_dict={X: X_test})
0 MSE: 502893.34
150 MSE: 13839.129
300 MSE: 3964.835
450 MSE: 2619.885
600 MSE: 2418.772
750 MSE: 2110.5923
900 MSE: 1887.9644
1050 MSE: 1747.1377
1200 MSE: 1556.3398
1350 MSE: 1384.6113
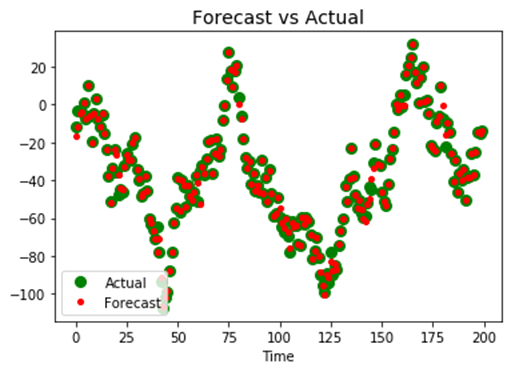
最后,在本 RNN 深度学习教程中,您可以绘制序列的实际值与预测值。如果您的模型正确,预测值应覆盖在实际值之上。
正如您所见,模型还有改进的空间。您可以自行更改超参数,例如窗口大小、批次大小或循环神经元数量。
plt.title("Forecast vs Actual", fontsize=14)
plt.plot(pd.Series(np.ravel(y_test)), "bo", markersize=8, label="Actual", color='green')
plt.plot(pd.Series(np.ravel(y_pred)), "r.", markersize=8, label="Forecast", color='red')
plt.legend(loc="lower left")
plt.xlabel("Time")
plt.show()
摘要
循环神经网络是一种处理时间序列或文本分析的强大架构。先前状态的输出被反馈回来,以在时间或单词序列中保留网络的记忆。
在 TensorFlow 中,您可以使用以下代码来训练用于时间序列的 TensorFlow 循环神经网络。
模型参数
n_windows = 20 n_input = 1 n_output = 1 size_train = 201
定义模型
X = tf.placeholder(tf.float32, [None, n_windows, n_input]) y = tf.placeholder(tf.float32, [None, n_windows, n_output]) basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=r_neuron, activation=tf.nn.relu) rnn_output, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32) stacked_rnn_output = tf.reshape(rnn_output, [-1, r_neuron]) stacked_outputs = tf.layers.dense(stacked_rnn_output, n_output) outputs = tf.reshape(stacked_outputs, [-1, n_windows, n_output])
构建优化
learning_rate = 0.001 loss = tf.reduce_sum(tf.square(outputs - y)) optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(loss)
训练模型
init = tf.global_variables_initializer()
iteration = 1500
with tf.Session() as sess:
init.run()
for iters in range(iteration):
sess.run(training_op, feed_dict={X: X_batches, y: y_batches})
if iters % 150 == 0:
mse = loss.eval(feed_dict={X: X_batches, y: y_batches})
print(iters, "\tMSE:", mse)
y_pred = sess.run(outputs, feed_dict={X: X_test})