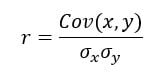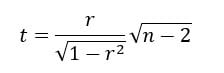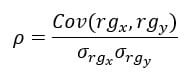R 中的相关性：皮尔逊和斯皮尔曼相关矩阵
Evelyn Clarke R 中的双变量相关性
双变量关系描述了 R 中两个变量之间的关系（或相关性）。在本教程中，我们将讨论相关性的概念，并展示如何使用它来衡量 R 中任何两个变量之间的关系。
R 编程中的相关性
在 R 编程中计算两个变量之间的相关性主要有两种方法。
- Pearson：参数相关性
- Spearman：非参数相关性
R 中的 Pearson 相关矩阵
Pearson 相关方法通常用作检查两个变量之间关系的初步方法。
相关系数 $r$ 是衡量两个变量 $X$ 和 $Y$ 之间线性关系强度的一种度量。计算方法如下：
与
$r = \frac{\sum_{i=1}^{n}(X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum_{i=1}^{n}(X_i - \bar{X})^2}\sqrt{\sum_{i=1}^{n}(Y_i - \bar{Y})^2}}$，即 $X$ 和 $Y$ 的标准差。
$r = \frac{\sum_{i=1}^{n}(X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum_{i=1}^{n}(X_i - \bar{X})^2}\sqrt{\sum_{i=1}^{n}(Y_i - \bar{Y})^2}}$，即 $X$ 和 $Y$ 的标准差。
$r = \frac{\sum_{i=1}^{n}(X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum_{i=1}^{n}(X_i - \bar{X})^2}\sqrt{\sum_{i=1}^{n}(Y_i - \bar{Y})^2}}$，即 $X$ 和 $Y$ 的标准差。
$r = \frac{\sum_{i=1}^{n}(X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum_{i=1}^{n}(X_i - \bar{X})^2}\sqrt{\sum_{i=1}^{n}(Y_i - \bar{Y})^2}}$，即 $X$ 和 $Y$ 的标准差。相关性范围在 -1 到 1 之间。
- 值接近或等于 0 意味着 $X$ 和 $Y$ 之间几乎没有线性关系。
- 相反，越接近 1 或 -1，线性关系越强。
我们可以按如下方式计算 t 检验，并查看自由度等于 $n-2$ 的分布表。
R 中的 Spearman 秩相关性
秩相关性通过秩对观测值进行排序，并计算秩之间的相似性程度。秩相关性的优点在于它对异常值具有鲁棒性，并且不与数据分布相关。请注意，秩相关性适用于有序变量。
Spearman 秩相关性 $rho$ 始终在 -1 和 1 之间，值接近极端值表示关系强。计算方法如下：
$rho = 1 - \frac{6 \sum d_i^2}{n(n^2-1)}$，其中 $d_i$ 是秩差，分母计算的是标准差。
在 R 中，我们可以使用 cor() 函数。它接受三个参数：x、y 和 method。
cor(x, y, method)
参数:
- x：第一个向量
- y：第二个向量
- method：用于计算相关性的公式。三个字符串值：
- “pearson”
- “kendall”
- “spearman”
如果向量包含缺失值，可以添加一个可选参数：use = “complete.obs”
我们将使用 BudgetUK 数据集。该数据集报告了英国家庭在 1980 年至 1982 年间的预算分配。有 1519 个观测值和十个特征，其中包括：
- wfood：食物支出份额
- wfuel：燃料支出份额
- wcloth：服装支出预算份额
- walc：酒精支出份额
- wtrans：交通支出份额
- wother：其他商品支出份额
- totexp：家庭总支出（英镑）
- income：家庭净收入总额
- age：家庭户主年龄
- children：子女数量
示例
library(dplyr)
PATH <-"https://raw.githubusercontent.com/guru99-edu/R-Programming/master/british_household.csv"
data <-read.csv(PATH)
filter(income < 500)
mutate(log_income = log(income),
log_totexp = log(totexp),
children_fac = factor(children, order = TRUE, labels = c("No", "Yes")))
select(-c(X,X.1, children, totexp, income))
glimpse(data)
代码解释
- 我们首先导入数据，并使用 dplyr 库中的 glimpse() 函数进行查看。
- 有三个点超过 500K，因此我们决定排除它们。
- 将货币变量转换为对数是常见的做法。这有助于减少异常值的影响，并减小数据集中的偏度。
输出
## Observations: 1,516## Variables: 10 ## $ wfood <dbl> 0.4272, 0.3739, 0.1941, 0.4438, 0.3331, 0.3752, 0... ## $ wfuel <dbl> 0.1342, 0.1686, 0.4056, 0.1258, 0.0824, 0.0481, 0... ## $ wcloth <dbl> 0.0000, 0.0091, 0.0012, 0.0539, 0.0399, 0.1170, 0... ## $ walc <dbl> 0.0106, 0.0825, 0.0513, 0.0397, 0.1571, 0.0210, 0... ## $ wtrans <dbl> 0.1458, 0.1215, 0.2063, 0.0652, 0.2403, 0.0955, 0... ## $ wother <dbl> 0.2822, 0.2444, 0.1415, 0.2716, 0.1473, 0.3431, 0... ## $ age <int> 25, 39, 47, 33, 31, 24, 46, 25, 30, 41, 48, 24, 2... ## $ log_income <dbl> 4.867534, 5.010635, 5.438079, 4.605170, 4.605170,... ## $ log_totexp <dbl> 3.912023, 4.499810, 5.192957, 4.382027, 4.499810,... ## $ children_fac <ord> Yes, Yes, Yes, Yes, No, No, No, No, No, No, Yes, ...
我们可以使用“pearson”和“spearman”方法计算 income 和 wfood 变量之间的相关系数。
cor(data$log_income, data$wfood, method = "pearson")
输出
## [1] -0.2466986
cor(data$log_income, data$wfood, method = "spearman")
输出
## [1] -0.2501252
R 中的相关矩阵
双变量相关性是一个不错的开始，但我们可以通过多变量分析获得更广阔的图景。许多变量的相关性在一个相关矩阵中显示。相关矩阵是表示所有变量成对相关性的矩阵。
cor() 函数返回一个相关矩阵。与双变量相关性唯一的不同是我们不需要指定变量。默认情况下，R 会计算所有变量之间的相关性。
请注意，不能为因子变量计算相关性。我们需要确保在将数据框传递给 cor() 之前删除分类特征。
相关矩阵是对称的，这意味着对角线上方的数值与下方的数值相同。显示矩阵的一半更具视觉效果。
我们排除了 children_fac，因为它是一个因子水平变量。cor 不对分类变量执行相关性计算。
# the last column of data is a factor level. We don't include it in the code mat_1 <-as.dist(round(cor(data[,1:9]),2)) mat_1
代码解释
- cor(data)：显示相关矩阵
- round(data, 2)：将相关矩阵四舍五入到两位小数
- as.dist()：仅显示后半部分
输出
## wfood wfuel wcloth walc wtrans wother age log_income ## wfuel 0.11 ## wcloth -0.33 -0.25 ## walc -0.12 -0.13 -0.09 ## wtrans -0.34 -0.16 -0.19 -0.22 ## wother -0.35 -0.14 -0.22 -0.12 -0.29 ## age 0.02 -0.05 0.04 -0.14 0.03 0.02 ## log_income -0.25 -0.12 0.10 0.04 0.06 0.13 0.23 ## log_totexp -0.50 -0.36 0.34 0.12 0.15 0.15 0.21 0.49
显著性水平
当使用 pearson 或 spearman 方法时，显著性水平在某些情况下很有用。Hmisc 库中的 rcorr() 函数为我们计算 p 值。我们可以从conda下载该库，并将代码复制到终端粘贴。
conda install -c r r-hmisc
rcorr() 要求将数据框存储为矩阵。我们可以先将数据转换为矩阵，然后再计算带 p 值的相关矩阵。
library("Hmisc")
data_rcorr <-as.matrix(data[, 1: 9])
mat_2 <-rcorr(data_rcorr)
# mat_2 <-rcorr(as.matrix(data)) returns the same output
mat_2 对象列表包含三个元素：
- r：相关矩阵的输出
- n：观测数量
- P：p 值
我们对第三个元素 p 值感兴趣。通常用 p 值而不是相关系数来显示相关矩阵。
p_value <-round(mat_2[["P"]], 3) p_value
代码解释
- mat_2[[“P”]]：p 值存储在名为 P 的元素中。
- round(mat_2[[“P”]], 3)：将元素四舍五入到三位小数。
输出
wfood wfuel wcloth walc wtrans wother age log_income log_totexp wfood NA 0.000 0.000 0.000 0.000 0.000 0.365 0.000 0 wfuel 0.000 NA 0.000 0.000 0.000 0.000 0.076 0.000 0 wcloth 0.000 0.000 NA 0.001 0.000 0.000 0.160 0.000 0 walc 0.000 0.000 0.001 NA 0.000 0.000 0.000 0.105 0 wtrans 0.000 0.000 0.000 0.000 NA 0.000 0.259 0.020 0 wother 0.000 0.000 0.000 0.000 0.000 NA 0.355 0.000 0 age 0.365 0.076 0.160 0.000 0.259 0.355 NA 0.000 0 log_income 0.000 0.000 0.000 0.105 0.020 0.000 0.000 NA 0 log_totexp 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 NA
R 中相关矩阵的可视化
热力图是显示相关矩阵的另一种方法。GGally 库是 ggplot2 的扩展。目前，它在 conda 库中不可用。我们可以在控制台中直接安装。
install.packages("GGally")
该库包含各种函数，用于在矩阵中显示所有变量的摘要统计信息，例如相关性和分布。
ggcorr() 函数有很多参数。在本教程中，我们将只介绍将使用的参数。
ggcorr 函数
ggcorr(df, method = c("pairwise", "pearson"),
nbreaks = NULL, digits = 2, low = "#3B9AB2",
mid = "#EEEEEE", high = "#F21A00",
geom = "tile", label = FALSE,
label_alpha = FALSE)
参数
- df：使用的数据集
- method：计算相关性的公式。默认情况下，计算成对 Pearson 相关性。
- nbreaks：为系数的着色返回一个分类范围。默认情况下，没有断点，颜色渐变是连续的。
- digits：四舍五入相关系数。默认设置为 2。
- low：控制着色的较低级别。
- mid：控制着色的中间级别。
- high：控制着色器的高级别。
- geom：控制几何参数的形状。默认值为“tile”。
- label：布尔值。显示或不显示标签。默认设置为 `FALSE`。
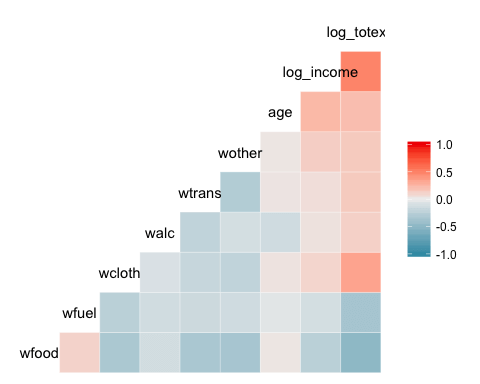
基本热力图
该包中最基本的情节是热力图。图形的图例显示了从 – 1 到 1 的颜色渐变，热颜色表示强正相关，冷颜色表示负相关。
library(GGally) ggcorr(data)
代码解释
- ggcorr(data)：只需要一个参数，即数据框名称。因子水平变量不包含在图中。
输出
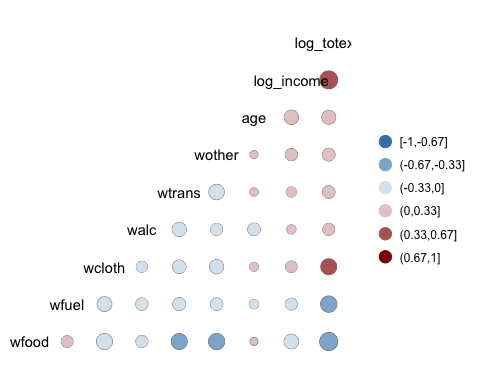
添加热力图控件
我们可以为图形添加更多控件。
ggcorr(data,
nbreaks = 6,
low = "steelblue",
mid = "white",
high = "darkred",
geom = "circle")
代码解释
- nbreaks=6：将图例分为 6 个等级。
- low = “steelblue”：对负相关使用较浅的颜色。
- mid = “white”：对中间范围的相关性使用白色。
- high = “darkred”：对正相关使用深色。
- geom = “circle”：将圆圈用作热力图窗口的形状。圆圈的大小与相关性的绝对值成正比。
输出
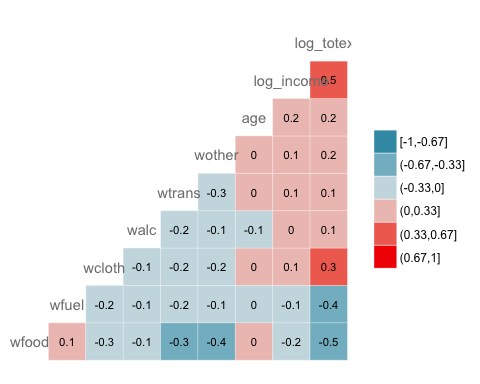
在热力图上添加标签
GGally 允许我们在窗口内添加标签。
ggcorr(data,
nbreaks = 6,
label = TRUE,
label_size = 3,
color = "grey50")
代码解释
- label = TRUE：在热力图内添加相关系数的值。
- color = “grey50”：选择颜色，例如灰色。
- label_size = 3：将标签大小设置为 3。
输出
ggpairs 函数
最后，我们介绍 GGaly 库中的另一个函数。Ggpair。它以矩阵格式生成图形。我们可以在一个图形中显示三种计算。该矩阵的维度是 $n \times n$，其中 $n$ 是观测数量。对角线上方的/下方的部分显示窗口。我们可以控制要在矩阵的每个部分显示哪些信息。ggpair 的公式为：
ggpair(df, columns = 1: ncol(df), title = NULL,
upper = list(continuous = "cor"),
lower = list(continuous = "smooth"),
mapping = NULL)
参数
- df：使用的数据集
- columns：选择用于绘制图形的列。
- title：包含一个标题。
- upper：控制图形对角线上的框。需要提供要返回的计算或图形的类型。如果 continuous = “cor”，我们要求 R 计算相关性。请注意，该参数需要是一个列表。其他参数也可以使用，请参阅文件了解更多信息。
- Lower：控制对角线以下的框。
- Mapping：指示图形的美学。例如，我们可以为不同的组计算图形。
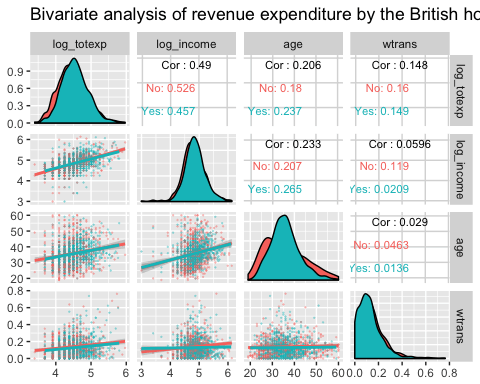
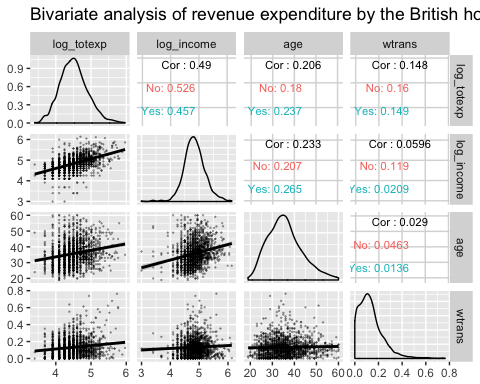
ggpair 的双变量分析（带分组）
下一个图形绘制了三个信息：
- 按家庭是否有孩子分组，log_totexp、log_income、age 和 wtrans 变量之间的相关矩阵。
- 按组绘制每个变量的分布图。
- 显示分组散点图和趋势线。
library(ggplot2)
ggpairs(data, columns = c("log_totexp", "log_income", "age", "wtrans"), title = "Bivariate analysis of revenue expenditure by the British household", upper = list(continuous = wrap("cor",
size = 3)),
lower = list(continuous = wrap("smooth",
alpha = 0.3,
size = 0.1)),
mapping = aes(color = children_fac))
代码解释
- columns = c(“log_totexp”, “log_income”, “age”, “wtrans”)：选择要在图形中显示的变量。
- title = “Bivariate analysis of revenue expenditure by the British household”：添加标题。
- upper = list()：控制图形的上半部分。即对角线上方。
- continuous = wrap(“cor”, size = 3))：计算相关系数。我们将 continuous 参数包装在 wrap() 函数中以控制图形的美学（即 size = 3）。 -lower = list()：控制图形的下半部分。即对角线下方。
- continuous = wrap(“smooth”,alpha = 0.3,size=0.1)：添加带线性趋势的散点图。我们将 continuous 参数包装在 wrap() 函数中以控制图形的美学（即 size=0.1, alpha=0.3）。
- mapping = aes(color = children_fac)：我们希望图形的每个部分按 children_fac 变量堆叠，children_fac 是一个分类变量，如果家庭没有孩子则取值为 1，否则取值为 2。
输出
ggpair 的双变量分析（带部分分组）
下图略有不同。我们已将 mapping 的位置移至 upper 参数内。
ggpairs(data, columns = c("log_totexp", "log_income", "age", "wtrans"),
title = "Bivariate analysis of revenue expenditure by the British household",
upper = list(continuous = wrap("cor",
size = 3),
mapping = aes(color = children_fac)),
lower = list(
continuous = wrap("smooth",
alpha = 0.3,
size = 0.1))
)
代码解释
- 与之前的示例代码完全相同，除了：
- mapping = aes(color = children_fac)：将列表移至 upper = list()。我们只希望在图形的上半部分按组堆叠计算。
输出
摘要
- 双变量关系描述了 R 中两个变量之间的关系（或相关性）。
- 在R 编程中计算两个变量之间的相关性主要有两种方法：Pearson 和 Spearman。
- Pearson 相关方法通常用作检查两个变量之间关系的初步方法。
- 秩相关性通过秩对观测值进行排序，并计算秩之间的相似性程度。
- Spearman 秩相关性 $rho$ 始终在 -1 和 1 之间，值接近极端值表示关系强。
- 相关矩阵是表示所有变量成对相关性的矩阵。
- 当使用 pearson 或 spearman 方法时，显著性水平在某些情况下很有用。
我们可以在下表中总结 R 中的所有相关函数。
| 库 | 目标 | 方法 | 代码 |
|---|---|---|---|
| 基础 | 双变量相关性 | Pearson |
cor(dfx2, method = "pearson") |
| 基础 | 双变量相关性 | Spearman |
cor(dfx2, method = "spearman") |
| 基础 | 多变量相关性 | Pearson |
cor(df, method = "pearson") |
| 基础 | 多变量相关性 | Spearman |
cor(df, method = "spearman") |
| Hmisc | p 值 |
rcorr(as.matrix(data[,1:9]))[["P"]] |
|
| Ggally | 热力图 |
ggcorr(df) |
|
| 多变量图 |
cf code below |
