Python矩阵:转置、乘法、NumPy数组示例
什么是 Python 矩阵?
Python 矩阵是一种专门的二维矩形数据数组,以行和列的形式存储。矩阵中的数据可以是数字、字符串、表达式、符号等。矩阵是可用于数学和科学计算的重要数据结构之一。
Python 矩阵如何工作?
矩阵格式的二维数组中的数据如下所示
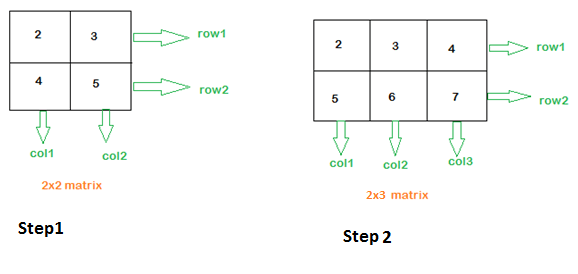
步骤 1) 显示一个 2×2 矩阵。它有两行两列。矩阵中的数据是数字。第一行值为 2,3,第二行值为 4,5。列,即第一列,值为 2,4,第二列值为 3,5。
步骤 2) 显示一个 2×3 矩阵。它有两行三列。第一行的值,即行 1,为 2,3,4,行 2 为 5,6,7。第一列值为 2,5,第二列值为 3,6,第三列值为 4,7。
因此,类似地,您可以将数据存储在 Python 的 nxn 矩阵中。矩阵可以执行许多操作,如加法、减法、乘法等。
Python 没有直接实现矩阵数据类型的方法。
Python 矩阵使用数组,并且可以实现这一点。
- 使用嵌套列表数据类型创建 Python 矩阵
- 使用 Python Numpy 包中的数组创建 Python 矩阵
使用嵌套列表数据类型创建 Python 矩阵
在 Python 中,数组用列表数据类型表示。所以现在我们将使用列表来创建一个 Python 矩阵。
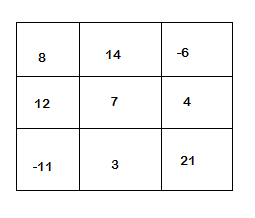
我们将创建一个 3×3 矩阵,如下所示
- 该矩阵有 3 行 3 列。
- 以列表格式的第一行如下:[8,14,-6]
- 第二行列表将是:[12,7,4]
- 第三行列表将是:[-11,3,21]
带所有行和列的列表中的矩阵如下所示
List = [[Row1],
[Row2],
[Row3]
...
[RowN]]
因此,根据上面的矩阵,列表类型的数据矩阵如下
M1 = [[8, 14, -6], [12,7,4], [-11,3,21]]
使用列表读取 Python 矩阵中的数据。
我们将使用上面定义的矩阵。示例将读取数据,打印矩阵,显示每行的最后一个元素。
示例:打印矩阵
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
#To print the matrix
print(M1)
输出
The Matrix M1 = [[8, 14, -6], [12, 7, 4], [-11, 3, 21]]
示例 2:读取每行的最后一个元素
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
matrix_length = len(M1)
#To read the last element from each row.
for i in range(matrix_length):
print(M1[i][-1])
输出
-6 4 21
示例 3:打印矩阵中的行
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
matrix_length = len(M1)
#To print the rows in the Matrix
for i in range(matrix_length):
print(M1[i])
输出
[8, 14, -6] [12, 7, 4] [-11, 3, 21]
使用嵌套列表进行矩阵加法
我们可以轻松地对两个给定的矩阵进行相加。这里的矩阵将是列表形式。让我们来看一个例子,它会处理相加给定的矩阵。
矩阵 1
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
矩阵 2
M2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
最后,我们将初始化一个矩阵来存储 M1 + M2 的结果。
矩阵 3
M3 = [[0,0,0],
[0,0,0],
[0,0,0]]
示例:矩阵相加
为了相加,我们将使用一个 for 循环,该循环会遍历给定的两个矩阵。
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
M2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
M3 = [[0,0,0],
[0,0,0],
[0,0,0]]
matrix_length = len(M1)
#To Add M1 and M2 matrices
for i in range(len(M1)):
for k in range(len(M2)):
M3[i][k] = M1[i][k] + M2[i][k]
#To Print the matrix
print("The sum of Matrix M1 and M2 = ", M3)
输出
The sum of Matrix M1 and M2 = [[11, 30, -12], [21, 14, 0], [-12, 6, 34]]
使用嵌套列表进行矩阵乘法
为了进行矩阵乘法,我们可以使用下面代码所示的对两个矩阵进行 for 循环
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
M2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
M3 = [[0,0,0],
[0,0,0],
[0,0,0]]
matrix_length = len(M1)
#To Multiply M1 and M2 matrices
for i in range(len(M1)):
for k in range(len(M2)):
M3[i][k] = M1[i][k] * M2[i][k]
#To Print the matrix
print("The multiplication of Matrix M1 and M2 = ", M3)
输出
The multiplication of Matrix M1 and M2 = [[24, 224, 36], [108, 49, -16], [11, 9, 273]]
使用 Python Numpy 包中的数组创建 Python 矩阵
Python 库 Numpy 有助于处理数组。与列表相比,Numpy 处理数组的速度稍快一些。
要使用 Numpy,您需要先安装它。请按照以下步骤安装 Numpy。
步骤 1) 安装 Numpy 的命令是
pip install NumPy
步骤 2) 要在代码中使用 Numpy,您需要导入它。
import NumPy
步骤 3) 您也可以使用别名导入 Numpy,如下所示
import NumPy as np
我们将使用 Numpy 的 array() 方法来创建 Python 矩阵。
示例:Numpy 中的数组用于创建 Python 矩阵
import numpy as np M1 = np.array([[5, -10, 15], [3, -6, 9], [-4, 8, 12]]) print(M1)
输出
[[ 5 -10 15] [ 3 -6 9] [ -4 8 12]]
使用 Numpy.Array() 进行矩阵运算
可以进行的矩阵运算包括加法、减法、乘法、转置、读取矩阵的行、列、矩阵切片等。在所有示例中,我们将使用 array() 方法。
矩阵加法
为了对矩阵进行加法运算,我们将使用 numpy.array() 创建两个矩阵,并使用 (+) 运算符将它们相加。
示例
import numpy as np M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]]) M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]]) M3 = M1 + M2 print(M3)
输出
[[ 12 -12 36] [ 16 12 48] [ 6 -12 60]]
矩阵减法
为了对矩阵进行减法运算,我们将使用 numpy.array() 创建两个矩阵,并使用 (-) 运算符将它们相减。
示例
import numpy as np M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]]) M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]]) M3 = M1 - M2 print(M3)
输出
[[ -6 24 -18] [ -6 -32 -18] [-20 40 -18]]
矩阵乘法
首先,我们将使用 numpy.arary() 创建两个矩阵。为了将它们相乘,您可以使用 numpy dot() 方法。Numpy.dot() 是矩阵 M1 和 M2 的点积。Numpy.dot() 处理 2D 数组并执行矩阵乘法。
示例
import numpy as np M1 = np.array([[3, 6], [5, -10]]) M2 = np.array([[9, -18], [11, 22]]) M3 = M1.dot(M2) print(M3)
输出
[[ 93 78] [ -65 -310]]
矩阵转置
矩阵的转置是通过将行更改为列并将列更改为行来计算的。Numpy 中的 transpose() 函数可用于计算矩阵的转置。
示例
import numpy as np M1 = np.array([[3, 6, 9], [5, -10, 15], [4,8,12]]) M2 = M1.transpose() print(M2)
输出
[[ 3 5 4] [ 6 -10 8] [ 9 15 12]]
矩阵切片
切片将根据给定的开始/结束索引从矩阵中返回元素。
- 切片的语法是 – [start:end]
- 如果未给出开始索引,则默认为 0。例如 [:5],表示 [0:5]。
- 如果未传递结束索引,则将使用数组的长度。
- 如果开始/结束具有负值,则将从数组末尾进行切片。
在处理矩阵切片之前,让我们先了解如何对简单数组应用切片。
import numpy as np arr = np.array([2,4,6,8,10,12,14,16]) print(arr[3:6]) # will print the elements from 3 to 5 print(arr[:5]) # will print the elements from 0 to 4 print(arr[2:]) # will print the elements from 2 to length of the array. print(arr[-5:-1]) # will print from the end i.e. -5 to -2 print(arr[:-1]) # will print from end i.e. 0 to -2
输出
[ 8 10 12] [ 2 4 6 8 10] [ 6 8 10 12 14 16] [ 8 10 12 14] [ 2 4 6 8 10 12 14]
现在让我们实现矩阵切片。要对矩阵进行切片
语法将是 M1[row_start:row_end, col_start:col_end]
- 第一个开始/结束用于行,即选择矩阵的行。
- 第二个开始/结束用于列,即选择矩阵的列。
我们将使用的矩阵 M1 如下
M1 = np.array([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
总共有 4 行。索引从 0 到 3。第 0 行是 [2,4,6,8,10],第 1 行是 [3,6,9,-12,-15],然后是第 2 行和第 3 行。
矩阵 M1 有 5 列。索引从 0 到 4。第 0 列的值为 [2,3,4,5],第 1 列的值为 [4,6,8,-10],然后是第 2、3、4、5 列。
这是一个示例,演示如何使用切片从矩阵中获取行和列数据。在此示例中,我们打印第 1 行和第 2 行,对于列,我们想要第 1、2、3 列。为了获得该输出,我们使用了:M1[1:3, 1:4]
示例
import numpy as np
M1 = np.array([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[1:3, 1:4]) # For 1:3, it will give first and second row.
#The columns will be taken from first to third.
输出
[[ 6 9 -12] [ 8 12 16]]
示例:打印所有行和第三列
import numpy as np
M1 = np.array([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:,3]) # This will print all rows and the third column data.
输出
[ 8 -12 16 -20]
示例:打印第一行和所有列
import numpy as np
M1 = np.array([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:1,]) # This will print first row and all columns
输出
[[ 2 4 6 8 10]]
示例:打印前三行和前 2 列
import numpy as np
M1 = np.array([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:3,:2])
输出
[[2 4] [3 6] [4 8]]
访问 NumPy 矩阵
我们已经看到了切片是如何工作的。考虑到这一点,我们将学习如何从矩阵中获取行和列。
打印矩阵的行
在本例中,我们将打印矩阵的行。
示例
import numpy as np M1 = np.array([[3, 6, 9], [5, -10, 15], [4,8,12]]) print(M1[0]) #first row print(M1[1]) # the second row print(M1[-1]) # -1 will print the last row
输出
[3 6 9] [ 5 -10 15] [ 4 8 12]
要获取最后一行,您可以使用索引或 -1。例如,矩阵有 3 行,
所以 M1[0] 将为您提供第一行,
M1[1] 将为您提供第二行
M1[2] 或 M1[-1] 将为您提供第三行或最后一行。
打印矩阵的列
import numpy as np
M1 = np.array([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:,0]) # Will print the first Column
print(M1[:,3]) # Will print the third Column
print(M1[:,-1]) # -1 will give you the last column
输出
[2 3 4 5] [ 8 -12 16 -20] [ 10 -15 -20 25]
摘要
- Python 矩阵是一种专门的二维矩形数据数组,以行和列的形式存储。矩阵中的数据可以是数字、字符串、表达式、符号等。矩阵是可用于数学和科学计算的重要数据结构之一。
- Python 没有直接实现矩阵数据类型的方法。Python 矩阵可以使用嵌套列表数据类型和 numpy 库来创建。
- Python 库 Numpy 有助于处理数组。与列表相比,Numpy 处理数组的速度稍快一些。
- 可以进行的矩阵运算包括加法、减法、乘法、转置、读取矩阵的行、列、矩阵切片等。
- 要对两个矩阵进行相加,您可以使用 numpy.array() 并使用 (+) 运算符将它们相加。
- 为了将它们相乘,您可以使用 numpy dot() 方法。Numpy.dot() 是矩阵 M1 和 M2 的点积。Numpy.dot() 处理 2D 数组并执行矩阵乘法。
- 矩阵的转置是通过将行更改为列并将列更改为行来计算的。Numpy 中的 transpose() 函数可用于计算矩阵的转置。
- 矩阵切片将根据给定的开始/结束索引为您返回元素。