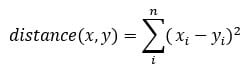R语言K-Means聚类及示例

什么是聚类分析？

聚类分析是无监督学习的一部分。聚类是数据中具有相似特征的组。我们可以说，聚类分析更多的是关于发现而不是预测。机器在数据中搜索相似性。例如，您可以使用聚类分析进行以下应用：

客户细分：寻找客户群之间的相似性
股市聚类：根据业绩对股票进行分组
通过将具有相似值的观测值分组来降低数据集的维度

聚类分析实现起来并不难，并且对企业来说既有意义又有可操作性。

监督学习和无监督学习之间最显著的区别在于结果。无监督学习创建一个新变量，即标签，而监督学习预测一个结果。机器帮助实践者根据密切相关性对数据进行标记。由分析师决定如何利用这些分组并为它们命名。

让我们举一个例子来理解聚类概念。为简单起见，我们在二维空间中进行。您拥有客户总支出和年龄的数据。为了改进广告，营销团队希望向其客户发送更有针对性的电子邮件。

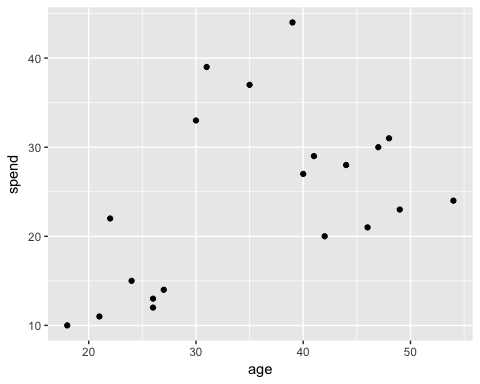
在下面的图中，您绘制了客户的总支出和年龄。

library(ggplot2)
df <- data.frame(age = c(18, 21, 22, 24, 26, 26, 27, 30, 31, 35, 39, 40, 41, 42, 44, 46, 47, 48, 49, 54),
    spend = c(10, 11, 22, 15, 12, 13, 14, 33, 39, 37, 44, 27, 29, 20, 28, 21, 30, 31, 23, 24)
)
ggplot(df, aes(x = age, y = spend)) +
    geom_point()

此时可以看到一个模式

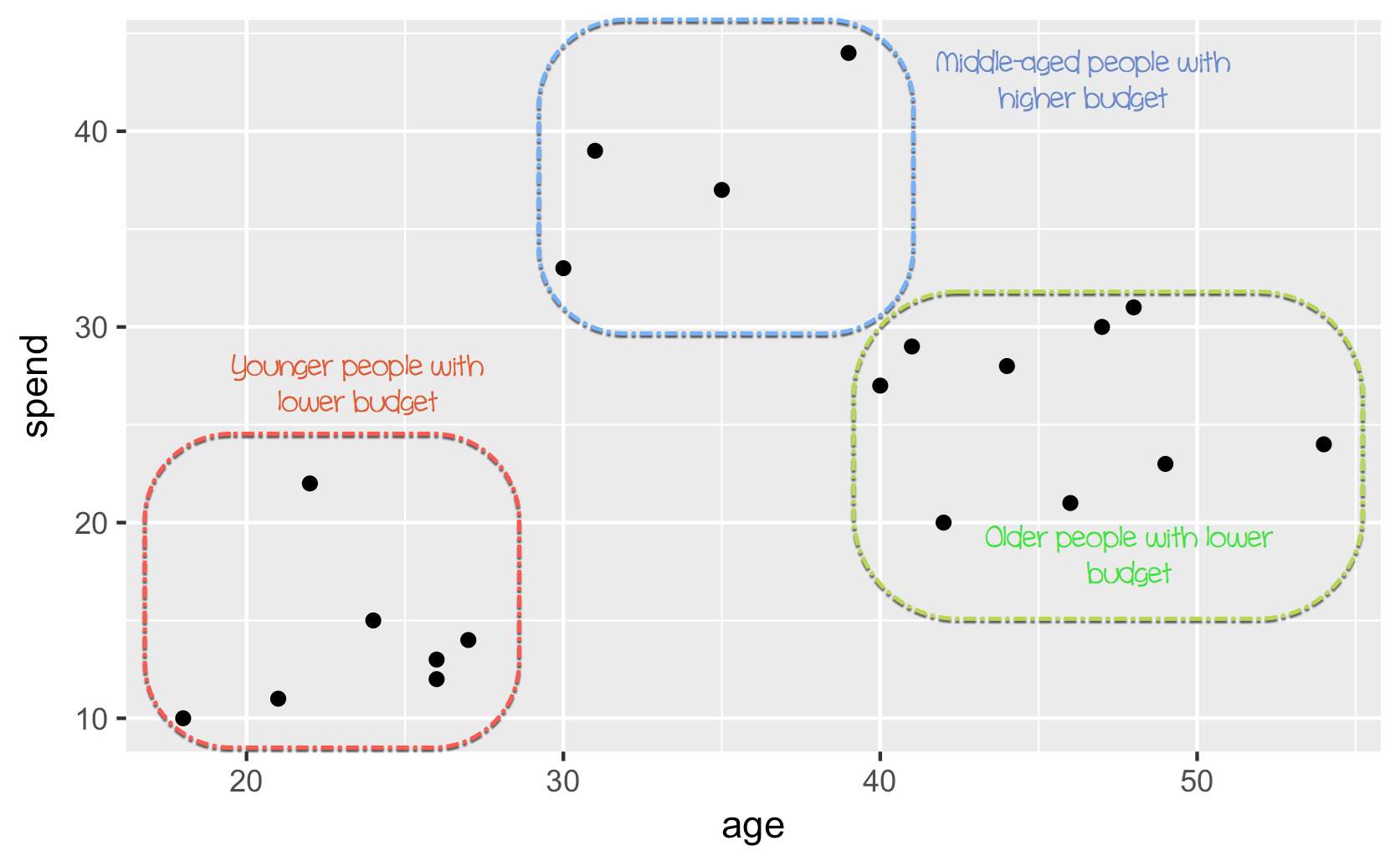
在左下角，您可以看到年轻人的购买力较低
中上部分反映了有工作的人，他们可以负担得起更多的支出
最后，老年人的预算较低。

在上图中，您手动聚类了观测值并定义了这三个组。这个例子有些简单且高度可视化。如果新观测值被添加到数据集中，您可以将它们标记在圆圈内。您根据自己的判断定义圆圈。相反，您可以使用机器学习来客观地分组数据。

在本教程中，您将学习如何使用k-means算法。

K-means 算法

K-means 无疑是最受欢迎的聚类方法。研究人员在几十年前就发布了该算法，并且对 k-means 进行了许多改进。

该算法试图通过最小化观测值之间的距离来寻找组，称为局部最优解。距离是根据观测值的坐标测量的。例如，在二维空间中，坐标是简单的 x 和 y。

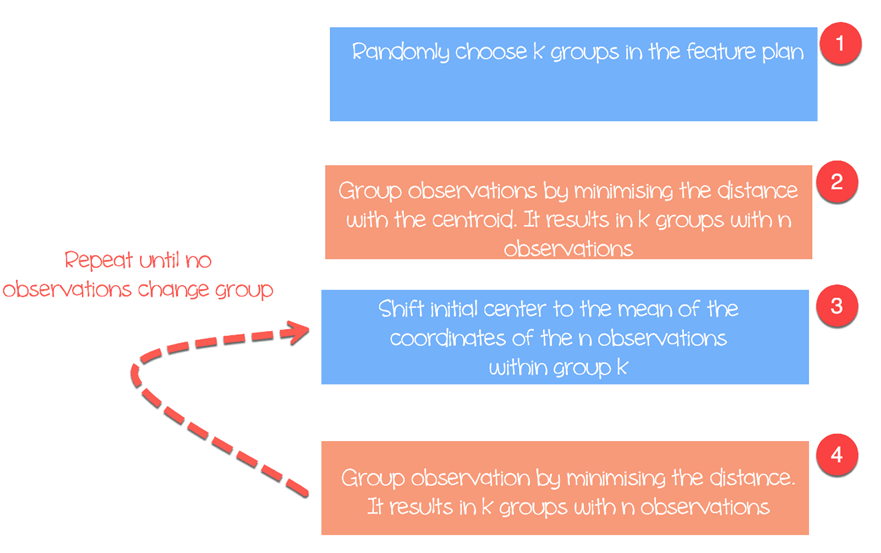
该算法如下工作：

步骤 1：在特征平面中随机选择组
步骤 2：最小化聚类中心与不同观测值（质心）之间的距离。这将导致形成包含观测值的组
步骤 3：将初始质心移动到组内坐标的均值。
步骤 4：根据新的质心最小化距离。创建了新的边界。因此，观测值将从一个组移动到另一个组。
重复直到没有观测值改变组

K-means 通常采用特征 x 和特征 y 之间的欧氏距离。

还有其他度量可用，例如曼哈顿距离或闵可夫斯基距离。请注意，每次运行算法时，K-mean 都会返回不同的组。回想一下，第一个初始猜测是随机的，并且算法计算距离直到达到组内的同质性。也就是说，k-mean 对第一个选择非常敏感，并且除非观测值数量和组数量较少，否则几乎不可能获得相同的聚类。

选择聚类数量

K-mean 的另一个难题是选择聚类数量。您可以设置较高的 k 值，即较多的组，以提高稳定性，但最终可能会导致数据过拟合。过拟合意味着模型在新的传入数据上的性能会显著下降。机器学会了数据集的细微差别，并努力概括整体模式。

聚类数量取决于数据集的性质、行业、业务等。但是，有一个经验法则可以帮助选择合适的聚类数量。

其中 n 是数据集中观测值的数量。

总的来说，花时间寻找最适合业务需求的 k 值是很有价值的。

我们将使用个人电脑价格数据集来执行我们的聚类分析。该数据集包含 6259 个观测值和 10 个特征。该数据集观察了 1993 年至 1995 年间美国 486 台个人电脑的价格。变量包括价格、速度、内存、屏幕、光驱等。

您将按以下步骤进行

导入数据
训练模型
评估模型

导入数据

K-means 不适用于因子变量，因为它基于距离，而离散值不会返回有意义的值。您可以删除我们数据集中这三个分类变量。此外，此数据集中没有缺失值。

library(dplyr)
PATH <-"https://raw.githubusercontent.com/guru99-edu/R-Programming/master/computers.csv"
df <- read.csv(PATH) %>%
select(-c(X, cd, multi, premium))
glimpse(df)

输出

## Observations: 6, 259
## Variables: 7
## $ price < int > 1499, 1795, 1595, 1849, 3295, 3695, 1720, 1995, 2225, 2...
##$ speed < int > 25, 33, 25, 25, 33, 66, 25, 50, 50, 50, 33, 66, 50, 25, ...
##$ hd < int > 80, 85, 170, 170, 340, 340, 170, 85, 210, 210, 170, 210...
##$ ram < int > 4, 2, 4, 8, 16, 16, 4, 2, 8, 4, 8, 8, 4, 8, 8, 4, 2, 4, ...
##$ screen < int > 14, 14, 15, 14, 14, 14, 14, 14, 14, 15, 15, 14, 14, 14, ...
##$ ads < int > 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, ...
## $ trend  <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1...

从汇总统计数据中，您可以看到数据具有大值。对于 k-means 和距离计算，一个好的做法是重新缩放数据，使均值等于 1，标准差等于 0。

summary(df)

输出

##      price          speed              hd              ram        
##  Min.   : 949   Min.   : 25.00   Min.   :  80.0   Min.   : 2.000  
##  1st Qu.:1794   1st Qu.: 33.00   1st Qu.: 214.0   1st Qu.: 4.000  `
##  Median :2144   Median : 50.00   Median : 340.0   Median : 8.000  
##  Mean   :2220   Mean   : 52.01   Mean   : 416.6   Mean   : 8.287  
##  3rd Qu.:2595   3rd Qu.: 66.00   3rd Qu.: 528.0   3rd Qu.: 8.000  
##  Max.   :5399   Max.   :100.00   Max.   :2100.0   Max.   :32.000  
##      screen           ads            trend      
##  Min.   :14.00   Min.   : 39.0   Min.   : 1.00  
##  1st Qu.:14.00   1st Qu.:162.5   1st Qu.:10.00  
##  Median :14.00   Median :246.0   Median :16.00  
##  Mean   :14.61   Mean   :221.3   Mean   :15.93  
##  3rd Qu.:15.00   3rd Qu.:275.0   3rd Qu.:21.50  
##  Max.   :17.00   Max.   :339.0   Max.   :35.00

您使用 dplyr 库的 scale() 函数重新缩放变量。这种转换减少了异常值的影响，并允许将单个观测值与均值进行比较。如果标准化值（或z 分数）很高，您可以确信该观测值确实高于均值（大的 z 分数意味着该点距离均值有几个标准差。z 分数为 2 表示该值距离均值有 2 个标准差。请注意，z 分数遵循高斯分布，并且围绕均值对称。

rescale_df <- df % > %
mutate(price_scal = scale(price),
    hd_scal = scale(hd),
    ram_scal = scale(ram),
    screen_scal = scale(screen),
    ads_scal = scale(ads),
    trend_scal = scale(trend)) % > %
select(-c(price, speed, hd, ram, screen, ads, trend))

R 基础有一个函数可以运行 k-means 算法。k-means 的基本函数是

kmeans(df, k)
arguments:
-df: dataset used to run the algorithm
-k: Number of clusters

训练模型

在图三中，您详细说明了算法的工作原理。您可以看到每个步骤的图形表示，这得益于 Yi Hui（也是 Knit for Rmarkdown 的创建者）构建的 great 包。动画包在 conda 库中不可用。您可以使用其他方法安装该包：install.packages(“animation”)。您可以检查该包是否已安装在我们的 Anaconda 文件夹中。

install.packages("animation")

加载库后，您只需在 kmeans 后面添加 .ani，R 就会绘制所有步骤。出于说明目的，我们仅使用重新缩放的变量 hd 和 ram 以及三个聚类来运行算法。

set.seed(2345)
library(animation)
kmeans.ani(rescale_df[2:3], 3)

代码解释

kmeans.ani(rescale_df[2:3], 3)：选择 rescale_df 数据集的第 2 列和第 3 列，并设置 k 为 3 来运行算法。绘制动画。

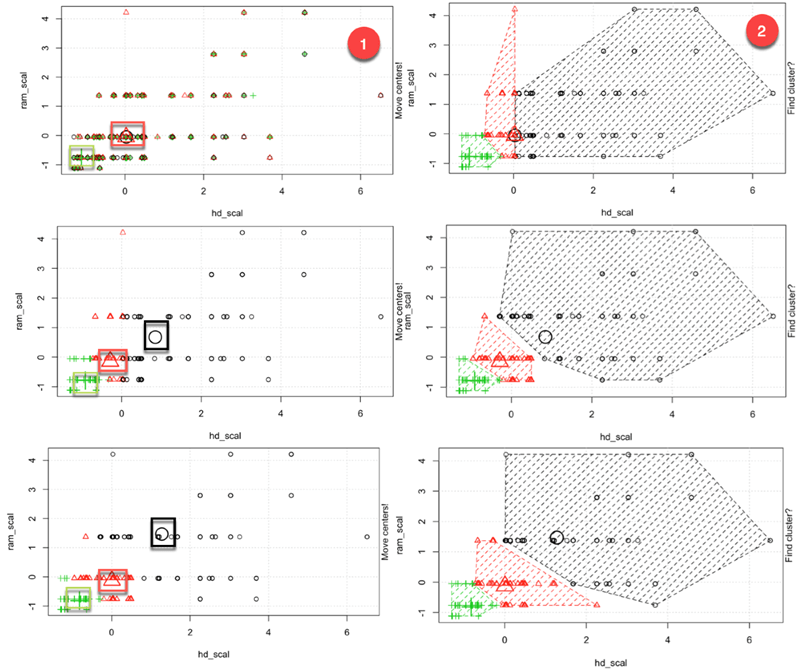
您可以这样解释动画：

步骤 1：R 随机选择三个点
步骤 2：计算欧氏距离并绘制聚类。您在左下角有一个绿色集群，右侧有一个大的黑色集群，它们之间有一个红色集群。
步骤 3：计算质心，即聚类的均值
重复直到没有数据改变聚类

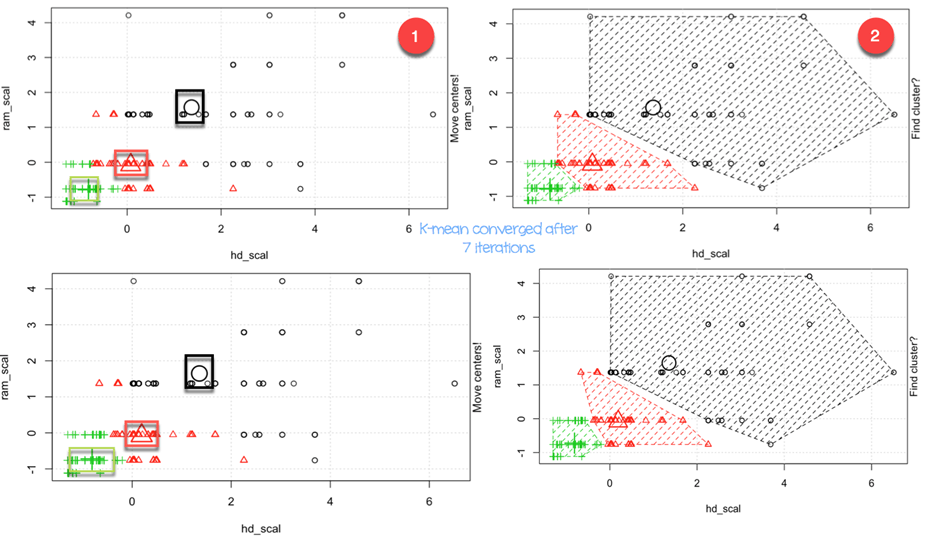
算法在七次迭代后收敛。您可以在我们的数据集中运行 k-means 算法，设置五个聚类，并将其命名为 pc_cluster。

pc_cluster <-kmeans(rescale_df, 5)

pc_cluster 列表包含七个有用的元素：
pc_cluster$cluster：指示每个观测值的聚类
pc_cluster$centers：聚类中心
pc_cluster$totss：总平方和
pc_cluster$withinss：组内平方和。返回的组件数量等于 `k`
pc_cluster$tot.withinss：组内平方和的总和
pc_cluster$betweenss：总平方和减去组内平方和
pc_cluster$size：每个聚类中的观测值数量

您将使用组内平方和的总和（即 tot.withinss）来计算最优聚类数量 k。寻找 k 确实是一项艰巨的任务。

最优 k

选择最佳 k 的一种技术称为肘部法则。该方法使用组内同质性或组内异质性来评估变异性。换句话说，您关心每个聚类解释的方差百分比。您可以预期随着聚类数量的增加，变异性会增加，或者换句话说，异质性会减少。我们的挑战是找到 k 值，该值超过了收益递减点。添加一个新聚类不会改进数据中的变异性，因为剩下的信息很少需要解释。

在本教程中，我们使用异质性度量来找到这一点。总组内平方和是 kmean() 返回列表中的 tot.withinss。

您可以像这样构建肘部图并找到最优 k：

步骤 1：构建一个函数来计算总组内平方和
步骤 2：运行算法 n 次
步骤 3：创建一个包含算法结果的数据框
步骤 4：绘制结果

步骤 1) 构建一个函数来计算总组内平方和

我们创建了一个运行 k-means 算法并存储总组内平方和的函数。

kmean_withinss <- function(k) {
    cluster <- kmeans(rescale_df, k)
    return (cluster$tot.withinss)
}

代码解释

function(k)：在函数中设置参数数量
kmeans(rescale_df, k)：运行算法 k 次
return(cluster$tot.withinss)：存储总组内平方和

您可以用 k=2 来测试该函数。

输出

## Try with 2 cluster

kmean_withinss(2)

输出

## [1] 27087.07

步骤 2) 运行算法 n 次

我们将使用 sapply() 函数在 k 的范围内运行算法。此技术比创建循环和存储值更快。

# Set maximum cluster 
max_k <-20 
# Run algorithm over a range of k 
wss <- sapply(2:max_k, kmean_withinss)

代码解释

max_k <-20：将最大 k 值设置为 20
sapply(2:max_k, kmean_withinss)：在 2:max_k 的范围内运行 kmean_withinss() 函数，即从 2 到 20。

步骤 3) 创建一个包含算法结果的数据框

在创建和测试函数后，您可以从 2 到 20 的范围内运行 k-means 算法，并存储 tot.withinss 值。

# Create a data frame to plot the graph
elbow <-data.frame(2:max_k, wss)

代码解释

data.frame(2:max_k, wss)：创建一个包含算法输出（存储在 wss 中）的数据框。

步骤 4) 绘制结果

我们绘制图表以可视化肘部点的位置。

# Plot the graph with gglop
ggplot(elbow, aes(x = X2.max_k, y = wss)) +
    geom_point() +
    geom_line() +
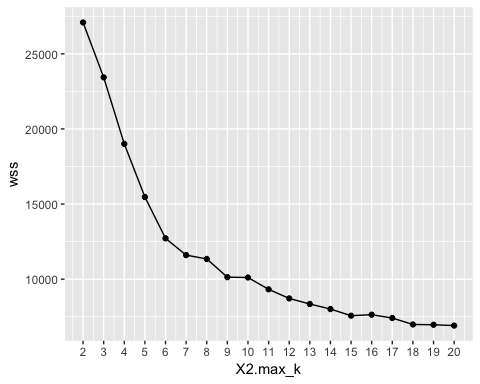
    scale_x_continuous(breaks = seq(1, 20, by = 1))

从图中可以看出，最优 k 是七，此时曲线开始出现收益递减。

一旦我们有了最优 k，我们就会用 k=7 重新运行算法并评估聚类。

检查聚类

pc_cluster_2 <-kmeans(rescale_df, 7)

如前所述，您可以访问 kmean() 返回列表中的其余有用信息。

pc_cluster_2$cluster
pc_cluster_2$centers
pc_cluster_2$size

评估部分是主观的，并且依赖于算法的使用。我们这里的目标是收集具有相似特征的计算机。计算机专家可以手动完成此任务，并根据他的专业知识对计算机进行分组。但是，这个过程将花费大量时间并且容易出错。K-means 算法可以为主机做好准备，通过建议聚类。

作为初步评估，您可以检查聚类的大小。

pc_cluster_2$size

输出

## [1] 608 1596 1231  580 1003  699  542

第一个聚类由 608 个观测值组成，而最小的聚类（编号 4）只有 580 台计算机。最好在聚类之间保持同质性，否则，可能需要进行更细致的数据准备。

我们通过中心分量更深入地了解数据。行对应于聚类的编号，列对应于算法使用的变量。值是每个聚类在感兴趣列上的平均得分。标准化使解释更容易。正值表示给定聚类的 z 分数高于总体均值。例如，聚类 2 的平均价格在所有聚类中是最高的。

center <-pc_cluster_2$centers
center

输出

##   price_scal    hd_scal     ram_scal screen_scal   ads_scal trend_scal
## 1 -0.6372457 -0.7097995 -0.691520682  -0.4401632  0.6780366 -0.3379751
## 2 -0.1323863  0.6299541  0.004786730   2.6419582 -0.8894946  1.2673184
## 3  0.8745816  0.2574164  0.513105797  -0.2003237  0.6734261 -0.3300536
## 4  1.0912296 -0.2401936  0.006526723   2.6419582  0.4704301 -0.4132057
## 5 -0.8155183  0.2814882 -0.307621003  -0.3205176 -0.9052979  1.2177279
## 6  0.8830191  2.1019454  2.168706085   0.4492922 -0.9035248  1.2069855
## 7  0.2215678 -0.7132577 -0.318050275  -0.3878782 -1.3206229 -1.5490909

我们可以使用 ggplot 创建热图，以帮助我们突出类别之间的差异。

ggplot 的默认颜色需要使用 RColorBrewer 库进行更改。您可以使用 conda 库和在终端中启动的代码

conda install -c r r-rcolorbrewer

创建热图需要三个步骤：

构建一个包含中心值的数据框，并创建一个包含聚类数量的变量。
使用 tidyr 库的 gather() 函数重塑数据。我们想将数据从宽格式转换为长格式。
使用 colorRampPalette() 函数创建颜色调色板。

步骤 1) 构建一个数据框

让我们创建重塑数据集。

library(tidyr)

# create dataset with the cluster number

cluster <- c(1: 7)
center_df <- data.frame(cluster, center)

# Reshape the data

center_reshape <- gather(center_df, features, values, price_scal: trend_scal)
head(center_reshape)

输出

##   cluster   features     values
## 1       1 price_scal -0.6372457
## 2       2 price_scal -0.1323863
## 3       3 price_scal  0.8745816
## 4       4 price_scal  1.0912296
## 5       5 price_scal -0.8155183
## 6       6 price_scal  0.8830191

步骤 2) 重塑数据

以下代码创建了我们将用于绘制热图的颜色调色板。

library(RColorBrewer)
# Create the palette
hm.palette <-colorRampPalette(rev(brewer.pal(10, 'RdYlGn')),space='Lab')

步骤 3) 可视化

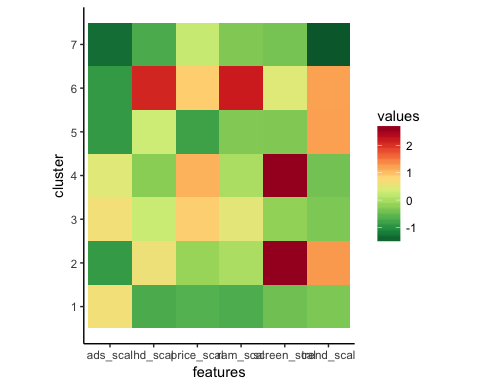
我们可以绘制图表并查看聚类的样子。

# Plot the heat map
ggplot(data = center_reshape, aes(x = features, y = cluster, fill = values)) +
    scale_y_continuous(breaks = seq(1, 7, by = 1)) +
    geom_tile() +
    coord_equal() +
    scale_fill_gradientn(colours = hm.palette(90)) +
    theme_classic()

摘要

我们可以在下表中总结 k-means 算法。

包	目标	函数	论证
base	训练 k-means	kmeans()	df, k
	访问聚类	kmeans()$cluster
	聚类中心	kmeans()$centers
	聚类大小	kmeans()$size

什么是聚类分析？

K-means 算法

选择聚类数量

相关文章

导入数据

训练模型

最优 k

检查聚类

摘要

订阅新闻通讯