边界值分析和等价划分

主要收获

• 在等价划分中，首先将一组测试条件划分为可考虑的几个分区。
• 在边界值分析中，您随后测试等价划分之间的边界。
• 适用于变量表示物理量且计算密集的应用程序
• 当实际上不可能单独测试大量测试用例时，可以使用边界分析测试

为什么要进行等价和边界分析测试

1. 此测试用于将大量测试用例减少到可管理的块。
2. 关于在不影响测试有效性的前提下确定测试用例的非常明确的指导方针。
3. 适用于变量/输入数量大且计算密集的应用程序

实际上，由于时间和预算的限制，不可能对每组测试数据进行详尽的测试，尤其是当存在大量输入组合时。

我们需要一种简便的方法或特殊技术，可以从测试用例池中智能地选择测试用例，以覆盖所有测试场景。我们使用两种技术来实现这一点——等价划分和边界值分析测试技术。

什么是边界测试？

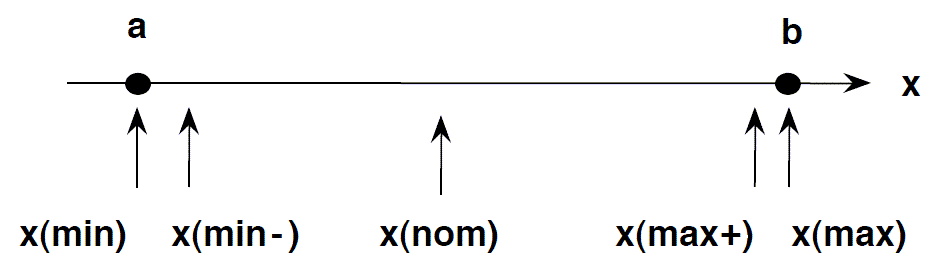
边界测试是对输入值分区之间的极端端点或边界进行测试的过程。

• 因此，这些极端端点，如开始-结束、下限-上限、最大值-最小值、刚好内部-刚好外部值，被称为边界值，这种测试被称为“边界测试”。
• 正常边界值测试的基本思想是选择输入变量值在其

1. 最小值
2. 略高于最小值
3. 一个标称值
4. 略低于最大值
5. 最大值

• 在边界测试中，等价类划分发挥着重要作用
• 边界测试是在等价类划分之后进行的。

等价划分

等价划分或等价类划分是一种黑盒测试技术，可以应用于所有级别的软件测试，如单元测试、集成测试、系统测试等。在这种技术中，输入数据单元被划分为等价分区，可用于推导测试用例，从而减少测试所需时间，因为测试用例数量较少。

• 它将软件的输入数据划分为不同的等价数据类。
• 您可以在输入字段存在范围的情况下应用此技术。

示例 1：等价和边界值

• 让我们考虑下面的“订购披萨”文本框的行为
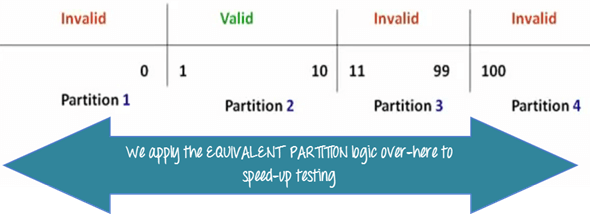
• 披萨数量 1 到 10 被认为是有效的。显示成功消息。
• 而值 11 到 99 被认为是无效订单，并会显示错误消息，“只能订购 10 个披萨”

这是测试条件

1. 在“订购披萨”字段中输入的任何大于 10 的数字（例如 11）都被视为无效。
2. 任何小于 1 的数字（即 0 或更小）都被视为无效。
3. 数字 1 到 10 被视为有效
4. 任何三位数（例如 -100）都是无效的。

我们无法测试所有可能的值，因为如果这样做，测试用例的数量将超过 100 个。为了解决这个问题，我们使用等价划分假设，我们将可能的票值分成如下图所示的组或集合，其中系统行为可以被认为是相同的。

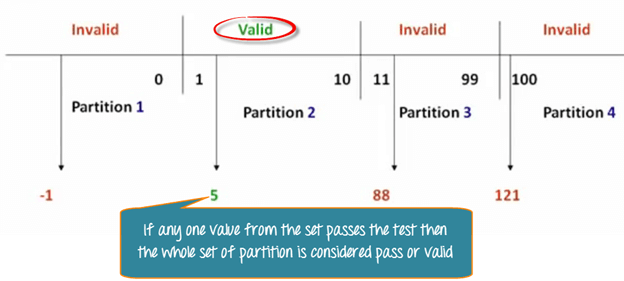
这些划分后的集合被称为等价分区或等价类。然后我们从每个分区中只选择一个值进行测试。这种技术背后的假设是，如果分区中的一个条件/值通过，所有其他条件也将通过。同样，如果分区中的一个条件失败，该分区中的所有其他条件都将失败。

边界值分析 – 在边界值分析中，您测试等价划分之间的边界

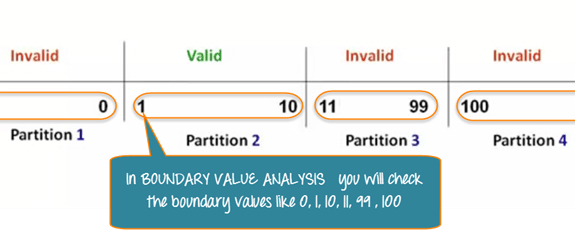
在我们之前的等价划分示例中，您将检查划分边界处的值，例如 0、1、10、11 等，而不是检查每个划分的一个值。正如您可能观察到的，您测试的是有效和无效边界处的值。边界值分析也称为范围检查。

等价划分和边界值分析（BVA）密切相关，可以一起用于所有测试级别。

示例 2：等价和边界值

以下密码字段接受最少 6 个字符和最多 10 个字符

这意味着分区 0-5、6-10、11-14 中的值的结果应该是等价的

测试场景 #	测试场景描述	预期结果
1	在密码字段中输入 0 到 5 个字符	系统不应接受
2	在密码字段中输入 6 到 10 个字符	系统应接受
3	在密码字段中输入 11 到 14 个字符	系统不应接受

示例 3：输入框应接受数字 1 到 10

这里我们将看到边界值测试用例

测试场景描述	预期结果
边界值 = 0	系统不应接受
边界值 = 1	系统应接受
边界值 = 2	系统应接受
边界值 = 9	系统应接受
边界值 = 10	系统应接受
边界值 = 11	系统不应接受

边界值分析和等价划分测试视频

如果视频无法访问，请点击此处