数据库中的关系代数:操作及示例
关系代数
关系代数是一种广泛使用的过程式查询语言。它以关系实例作为输入,以关系实例作为输出。它使用各种操作来执行此操作。SQL关系代数查询操作以递归方式对关系执行。这些操作的输出是一个新的关系,它可能由一个或多个输入关系组成。
基本 SQL 关系代数操作
关系代数分为几类
单目关系操作
- 选择 (符号:σ)
- 投影 (符号:π)
- 重命名 (符号:ρ)
集合论中的关系代数操作
- 并集 (υ)
- 交集 ( ),
- 差集 (-)
- 笛卡尔积 ( x )
二目关系操作
- 连接
- 除法
让我们通过示例和解决方案详细学习它们
选择 (σ)
SELECT 操作用于根据给定的选择条件选择元组的子集。Sigma(σ)符号表示它。它用作表达式来选择满足选择条件的元组。Select 操作符选择满足给定谓词的元组。
σp(r)
σ 是谓词
r 代表关系,即表的名称
p 是命题逻辑
示例 1
σ topic = "Database" (Tutorials)
输出 – 从 Tutorials 中选择主题为“Database”的元组。
示例 2
σ topic = "Database" and author = "guru99"( Tutorials)
输出 – 从 Tutorials 中选择主题为“Database”且“author”为 guru99 的元组。
示例 3
σ sales > 50000 (Customers)
输出 – 从 Customers 中选择销售额大于 50000 的元组。
投影(π)
投影操作会删除输入关系中的所有属性,只保留投影列表中的属性。投影方法定义了一个包含关系垂直子集的关系。
这有助于提取指定属性的值,并消除重复值。(pi)符号用于从关系中选择属性。此操作符帮助您保留关系中的特定列,并丢弃其他列。
投影示例
考虑下表
| CustomerID | CustomerName | 状态 |
|---|---|---|
| 1 | 活跃 | |
| 2 | Amazon | 活跃 |
| 3 | Apple | 不活跃 |
| 4 | 阿里巴巴 | 活跃 |
这里,CustomerName 和 status 的投影将得到
Π CustomerName, Status (Customers)
| CustomerName | 状态 |
|---|---|
| 活跃 | |
| Amazon | 活跃 |
| Apple | 不活跃 |
| 阿里巴巴 | 活跃 |
重命名 (ρ)
重命名是一种用于重命名关系属性的单目操作。
ρ (a/b)R 将把关系中的属性‘b’重命名为‘a’。
并集操作 (υ)
并集用 ∪ 符号表示。它包含表 A 或表 B 中的所有元组。它还会删除重复的元组。因此,集合 A 并集集合 B 可以表示为
结果 <- A ∪ B
为了使并集操作有效,必须满足以下条件 –
- R 和 S 必须具有相同数量的属性。
- 属性域需要兼容。
- 重复元组应自动删除。
示例
考虑以下表格。
| 列 1 | 列 2 | 列 1 | 列 2 | |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | |
| 1 | 2 | 1 | 3 | |
A ∪ B 得到
| 列 1 | 列 2 |
|---|---|
| 1 | 1 |
| 1 | 2 |
| 1 | 3 |
差集 (-)
– 符号表示它。A – B 的结果是包含 A 中存在但 B 中不存在的所有元组的关系。
- A 的属性名称必须与 B 中的属性名称匹配。
- 两个操作数关系 A 和 B 应兼容或并集兼容。
- 它应该被定义为包含关系 A 中存在但 B 中不存在的元组的关系。
示例
A-B
| 列 1 | 列 2 |
|---|---|
| 1 | 2 |
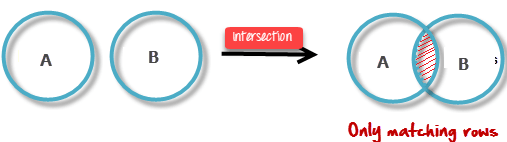
交集
交集由符号 ∩ 定义
A ∩ B
定义一个关系,其中包含同时存在于 A 和 B 中的所有元组。但是,A 和 B 必须是并集兼容的。
示例
A ∩ B
| 列 1 | 列 2 |
|---|---|
| 1 | 1 |
DBMS 中的笛卡尔积(X)
DBMS 中的笛卡尔积是一种用于合并来自两个关系的列的操作。通常,当笛卡尔积单独执行时,它没有意义。但是,当它后面跟其他操作时,它就变得有意义了。它也称为交叉乘积或交叉连接。
示例 – 笛卡尔积
σ column 2 = ‘1’ (A X B)
输出 – 上面的示例显示了关系 A 和 B 中 column 2 的值为 1 的所有行。
| 列 1 | 列 2 |
|---|---|
| 1 | 1 |
| 1 | 1 |
连接操作
连接操作本质上是笛卡尔积后面跟着一个选择条件。
连接操作用 ⋈ 表示。
JOIN 操作还允许连接不同关系中各种相关联的元组。
JOIN 类型
连接操作有多种形式
内连接
- Theta join
- EQUI join
- Natural join
外连接
- 左外连接
- Right Outer Join
- Full Outer Join
内连接 (Inner Join)
在内连接中,只包含满足匹配条件的元组,而其余的则被排除。我们来学习各种类型的内连接。
Theta Join
JOIN 操作的一般情况称为 Theta join。它用符号 θ 表示。
示例
A ⋈θ B
Theta join 可以在选择条件中使用任何条件。
例如
A ⋈ A.column 2 > B.column 2 (B)
| 列 1 | 列 2 |
|---|---|
| 1 | 2 |
EQUI join
当 Theta join 只使用相等条件时,它就成为等值连接。
例如
A ⋈ A.column 2 = B.column 2 (B)
| 列 1 | 列 2 |
|---|---|
| 1 | 1 |
EQUI join 是使用 SQL 在 RDBMS 中高效实现的难度最大的操作之一,也是 RDBMS 存在基本性能问题的原因之一。
自然连接 (⋈)
自然连接只能在关系之间存在公共属性(列)时执行。属性的名称和类型必须相同。
示例
考虑以下两个表
| 号码 | 平方 |
|---|---|
| 2 | 4 |
| 3 | 9 |
| 号码 | Cube |
|---|---|
| 2 | 8 |
| 3 | 27 |
C ⋈ D
| 号码 | 平方 | Cube |
|---|---|---|
| 2 | 4 | 8 |
| 3 | 9 | 27 |
外连接
在外连接中,除了满足匹配条件的元组之外,我们还包含一些或所有不满足条件的元组。
左外连接(A ⟕ B)
在左外连接中,操作允许保留左关系中的所有元组。但是,如果在右关系中未找到匹配的元组,则连接结果中的右关系属性将用 NULL 值填充。
考虑以下 2 个表
| 号码 | 平方 |
|---|---|
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 号码 | Cube |
|---|---|
| 2 | 8 |
| 3 | 18 |
| 5 | 75 |
AB
| 号码 | 平方 | Cube |
|---|---|---|
| 2 | 4 | 8 |
| 3 | 9 | 18 |
| 4 | 16 | – |
右外连接 ( A ⟖ B )
在右外连接中,操作允许保留右关系中的所有元组。但是,如果在左关系中未找到匹配的元组,则连接结果中的左关系属性将用 NULL 值填充。
AB
| 号码 | Cube | 平方 |
|---|---|---|
| 2 | 8 | 4 |
| 3 | 18 | 9 |
| 5 | 75 | – |
全外连接 ( A ⟗ B)
在全外连接中,无论匹配条件如何,两个关系中的所有元组都将包含在结果中。
AB
| 号码 | Cube | 平方 |
|---|---|---|
| 2 | 4 | 8 |
| 3 | 9 | 18 |
| 4 | 16 | – |
| 5 | – | 75 |
摘要
| 操作(符号) | 目的 |
|---|---|
| 选择(σ) | SELECT 操作用于根据给定的选择条件选择元组的子集。 |
| 投影(π) | 投影操作会删除输入关系中的所有属性,只保留投影列表中的属性。 |
| 并集操作(∪) | 并集用符号表示。它包含表 A 或表 B 中的所有元组。 |
| 差集(-) | – 符号表示它。A – B 的结果是包含 A 中存在但 B 中不存在的所有元组的关系。 |
| 交集(∩) | 交集定义了一个关系,其中包含同时存在于 A 和 B 中的所有元组。 |
| 笛卡尔积(X) | 笛卡尔操作有助于合并两个关系中的列。 |
| 内连接 (Inner Join) | 内连接,只包含满足匹配条件的元组。 |
| Theta Join(θ) | JOIN 操作的一般情况称为 Theta join。它用符号 θ 表示。 |
| EQUI Join | 当 Theta join 只使用相等条件时,它就成为等值连接。 |
| 自然连接(⋈) | 自然连接只能在关系之间存在公共属性(列)时执行。 |
| 外连接 (Outer Join) | 在外连接中,除了满足匹配条件的元组之外。 |
| 左外连接( |
在左外连接中,操作允许保留左关系中的所有元组。 |
| 右外连接( |
在右外连接中,操作允许保留右关系中的所有元组。 |
| 全外连接( |
在全外连接中,无论匹配条件如何,两个关系中的所有元组都将包含在结果中。 |


