汉明码：带示例的错误检测和纠正

什么是错误？

在通信过程中，传输的数据可能会损坏。它很可能受到外部噪声或其他物理故障的影响。在这种情况下，输入数据可能与输出数据不同。这种不匹配被称为“错误”。

数据错误可能导致重要或安全数据丢失。数字系统中的大多数数据传输将以“比特传输”的形式进行。即使是一个小比特的改变也会影响整个系统的性能。在数据序列中，如果1变为0或0变为1，则称为“比特错误”。

错误类型

在数据从发送方传输到接收方的过程中，主要有三种比特错误会发生。

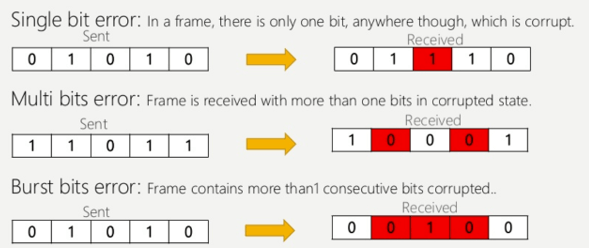
单比特错误
多比特错误
突发错误

单比特错误

在整个数据序列中，一个比特发生的改变称为“单比特错误”。但是，单比特错误的发生并不常见。此外，这种错误只发生在并行通信系统中，因为数据是逐比特在单条线路上传输的。因此，单条线路有更大的可能出现噪声。

多比特错误

在数据序列中，如果从发送方到接收方的数据序列中的两个或多个比特发生改变，则称为“多比特错误”。

这种类型的错误主要发生在串行和并行数据通信网络中。

突发错误

数据序列中一组比特的改变称为“突发错误”。这种数据错误是从第一次比特改变到最后一次比特改变来计算的。

什么是错误检测与错误纠正？

在数字通信系统中，错误会从一个通信系统传输到另一个通信系统。如果这些错误未被检测和纠正，则数据将丢失。为了有效通信，系统数据应以高精度传输。这可以通过先识别错误再纠正它们来完成。

错误检测是检测数据通信系统中从发送方到接收方传输的数据中存在的错误的方法。

在这里，您可以使用冗余码来查找这些错误，方法是在数据传输时添加冗余码。这些码称为“错误检测码”。

三种类型的错误检测码是：

奇偶校验
循环冗余校验 (CRC)
纵向冗余校验 (LRC)

奇偶校验

它也称为奇偶校验。
它具有成本效益的错误检测机制。
在此技术中，冗余比特称为奇偶比特。它附加到每个数据单元。单元中1的总数应为偶数，这称为奇偶比特。

纵向冗余校验

在此错误检测技术中，一组比特以表格格式组织。LRC 方法帮助您计算每列的奇偶比特。这组奇偶校验信息也与原始数据一起发送。奇偶校验块有助于检查冗余。

循环冗余校验

循环冗余校验是一组冗余码，必须附加到单元末尾。因此，结果数据单元应能被第二个预设的二进制数整除。

在目的地，需要用相同的数字除以传入的数据。如果没有余数，则假定数据单元是正确的并被接受。否则，它表示数据单元在传输过程中已损坏，因此必须将其拒绝。

什么是汉明码？

汉明码是一种线性码，可用于检测多达两个连续比特错误。它可以处理单比特错误。

在汉明码中，发送方通过在消息中添加冗余比特来编码消息。这些冗余比特主要插入并生成在消息的特定位置，以完成错误检测和纠正过程。

汉明码的历史

汉明码是由 R.W. Hamming 创建的一种用于检测错误的技术。
汉明码应应用于任意长度的数据单元，并利用数据和冗余比特之间的关系。
他致力于纠错方法的研究，并开发了一系列日益强大的算法，称为汉明码。
1950 年，他发表了汉明码，如今广泛应用于 ECC 内存等领域。

汉明码的应用

以下是使用汉明码的一些常见应用：

卫星
计算机内存
调制解调器
PlasmaCAM
开放连接器
屏蔽线
嵌入式处理器

汉明码的优点

汉明码方法在数据流仅针对单比特错误的网络上非常有效。
汉明码不仅可以检测比特错误，还可以帮助您识别包含错误的比特，以便进行纠正。
汉明码的易用性使其非常适合用于计算机内存和单比特纠错。

汉明码的缺点

单比特错误检测和纠正码。但是，如果检测到多个比特错误，则结果可能导致另一个本应正确的比特被改变。这可能导致数据进一步出错。
汉明码算法只能解决单比特问题。

如何用汉明码编码消息

发送方用于编码消息的过程包括以下三个步骤：

计算冗余比特的总数。
检查冗余比特的位置。
最后，计算这些冗余比特的值。

当上述冗余比特嵌入到消息中后，就会发送给用户。

第一步）计算冗余比特的总数。

假设消息包含：

n – 数据比特数
p – 添加的冗余比特数，以便 np 至少可以指示 (n + p + 1) 个不同的状态。

这里，(n + p) 表示在 (n + p) 个比特位置中的每一个位置上发生的错误，还有一个额外状态表示没有错误。由于 p 个比特可以表示 2^p 个状态，因此 2^p 必须至少等于 (n + p + 1)。

第二步）将冗余比特放置在正确的位置。

p 个冗余比特应放置在 2 的幂次方的位置。例如，1、2、4、8、16 等。它们分别被称为 p₁（位置 1）、p₂（位置 2）、p₃（位置 4）等。

第三步）计算冗余比特的值。

冗余比特应为奇偶比特，使 1 的数量变为偶数或奇数。

两种奇偶校验是？

消息的总比特数变为偶数称为偶校验。
消息的总比特数变为奇数称为奇校验。

在这里，所有冗余比特 p1 都必须计算为奇偶校验。它应覆盖所有二进制表示包含 1 的比特位置，但不包括 p1 的位置。

P1 是每个数据比特的奇偶比特，位于二进制表示包含 1 的位置，但不包括 1（例如 3、5、7、9...）

P2 是每个数据比特的奇偶比特，位于二进制表示包含从右数第 2 个位置为 1 的位置，但不包括 2（例如 3、6、7、10、11...）

P3 是每个数据比特的奇偶比特，位于二进制表示包含从右数第 3 个位置为 1 的位置，但不包括 4（例如 5-7、12-15...）

用汉明码解密消息

接收方接收到传入的消息，需要执行重新计算以查找和纠正错误。

重新计算过程按以下步骤进行：

计算冗余比特的数量。
正确放置所有冗余比特。
奇偶校验

第一步）计算冗余比特的数量

您可以为编码使用相同的公式，冗余比特的数量为：

2^p ≥ n + p + 1

这里，n 是数据比特数，p 是冗余比特数。

第二步）正确放置所有冗余比特

这里，p 是冗余比特，位于 2 的幂次方的位置，例如 1、2、4、8 等。

第三步）奇偶校验

奇偶比特需要根据数据比特和冗余比特进行计算。

p1 = parity(1, 3, 5, 7, 9, 11…)

p2 = parity(2, 3, 6, 7, 10, 11…)

p3 = parity(4-7, 12-15, 20-23…)

摘要

传输的数据在通信过程中可能会损坏
三种比特错误是：1）单比特错误 2）多比特错误 3）突发比特错误
在整个数据序列中，一个比特发生的改变称为“单比特错误”。
在数据序列中，如果从发送方到接收方的数据序列中的两个或多个比特发生改变，则称为“多比特错误”。
数据序列中一组比特的改变称为“突发错误”。
错误检测是检测数据通信系统中从发送方到接收方传输的数据中存在的错误的方法
三种类型的错误检测码是：1）奇偶校验 2）循环冗余校验 (CRC) 3）纵向冗余校验 (LRC)
汉明码是一种线性码，可用于检测多达两个连续比特错误。它可以处理单比特错误。
汉明码是由 R.W. Hamming 创建的一种用于检测错误的技术。
汉明码的常见应用包括卫星、计算机内存、调制解调器、嵌入式处理器等。
汉明码方法最大的好处是它在数据流仅针对单比特错误的网络上非常有效。
汉明码方法最大的缺点是它只能解决单比特问题。
我们可以借助汉明码执行消息的加密和解密过程。